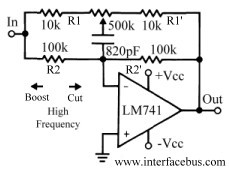
Audio Equalizer Circuits

1. What is Audio Equalization?

1.1 What is Audio Equalization?

Audio equalization is a critical process in the manipulation of audio signals, allowing for the adjustment of specific frequency ranges to enhance sound quality or meet particular sonic requirements. This procedure is central to both recording and live sound environments, influencing how an audio piece is perceived by the listener. At its core, equalization involves the alteration of an audio signal’s amplitude at various frequency bands, thereby shaping its tonal balance.

Historically, equalization dates back to the early days of radio broadcasting, where tone controls were implemented to compensate for limitations in transmission fidelity. As technology progressed into the digital realm, equalization became more sophisticated, leading to the development of various types of equalizers, including graphic, parametric, and shelving types. These advancements enable sound engineers to tailor their audio output with precision, taking into account the acoustics of the space and the characteristics of the equipment used.

The Principles of Audio Equalization

The fundamental principle behind equalization lies in its ability to modify an audio signal’s spectrum. An audio signal can be mathematically represented in the frequency domain using the Fourier Transform, which decomposes a time-domain signal into its constituent frequencies. This allows for the identification of specific frequency ranges that may need adjustment, typically represented as filters.

Filters can be categorized broadly into several types:

Low-pass filters: Allow frequencies below a certain cutoff frequency to pass through while attenuating higher frequencies.
High-pass filters: Do the opposite, permitting higher frequencies to pass and reducing lower frequencies.
Band-pass filters: Combine both low-pass and high-pass characteristics, allowing a specific range of frequencies to pass while attenuating those outside the range.
Notch filters: Specifically attenuate a narrow frequency band, effectively removing troublesome resonances.

Mathematical Representation of Equalization

To delve deeper, consider the transfer function of a typical filter, which can be expressed as:

$$ H(f) = \frac{Y(f)}{X(f)} $$

Here, $H(f)$ represents the transfer function, $Y(f)$ is the Fourier transform of the output signal, and $X(f)$ is the Fourier transform of the input signal. By manipulating $H(f)$, one can shape the frequencies present in the output signal, which can be computed and applied using digital signal processing (DSP).

Within an audio equalizer, these transfer functions can be combined to achieve a specific tonal balance. By employing various filters at different frequency bands, a sound engineer can significantly alter the audio signal without introducing unwanted distortion.

Practical Applications of Equalization

In practice, audio equalizers are employed across numerous applications:

Live sound reinforcement: Equalization is used to adapt sound systems to the acoustics of a venue, ensuring clear and balanced audio output.
Studio mixing: Engineers utilize equalizers to fine-tune the individual tracks, balancing each instrument's presence in the final mix.
Broadcasting: Equalization is vital in maintaining audio consistency across different mediums, from radio to television broadcasts.

As technology advances, the role of equalization continues to evolve, with sophisticated software-based equalizers providing unprecedented control over audio analysis and manipulation. Understanding the principles of audio equalization not only enhances the effectiveness of audio engineering practices but also enriches the overall listening experience.

Diagram Description: The diagram would illustrate the frequency response of different types of filters (low-pass, high-pass, band-pass, and notch), visually showing how each filter modifies the amplitude of various frequency components. This representation would clarify their operational differences and the concept of frequency modification in equalization.

1.2 Importance of Equalization in Audio Engineering

The role of equalization in audio engineering is pivotal, shaping both the technical and aesthetic aspects of sound reproduction. As engineers, our goal is not merely to amplify or attenuate specific frequencies but to sculpt the auditory experience to achieve clarity, balance, and emotional impact. Equalization serves as a critical tool in accomplishing this, allowing for the manipulation of sound in various contexts, from live performances to studio recordings.

Understanding Equalization

At its core, equalization involves the adjustment of the amplitude of specific frequency bands within an audio signal. This manipulation can compensate for deficiencies in recording equipment, acoustics of the environment, or listener preferences. A well-crafted equalization curve can enhance the perceived quality of sound, ensuring that each instrument and vocal track occupies its own sonic space. In technical terms, equalizers can be categorized as either linear phase or minimum phase filters. Linear phase equalizers maintain the phase relationship of the frequencies while introducing minimal distortion, making them ideal for mastering applications. Conversely, minimum phase equalizers are more suited for real-time adjustments, especially during mixing, as they introduce phase shifts but provide a more immediate response to changes in frequency.

Practical Applications of Equalization

Equalization finds its application in numerous scenarios, including:

Mixing Music: In a mix, each instrument's frequency content must be balanced. For example, boosting the mid-range frequencies of vocals can help them cut through a dense mix.
Live Sound Reinforcement: During live performances, equalizers are critical in adapting to changing acoustical environments, preventing feedback, and ensuring the audio system's output is clear and balanced.
Broadcasting: In radio and television broadcasts, equalization ensures that audio content is consistently broadcasted at optimal levels across different media formats.

The foundation of effective equalization lies in understanding frequency response, which describes how an audio device or environment responds to different frequencies. The frequency response curve is represented graphically, showing how amplitude varies across the frequency spectrum. It can directly influence how music is perceived; thus, recognizing the nuances in these curves helps audio engineers create a more engaging listening experience.

Historical Development of Equalization Techniques

Historically, equalization emerged from the need to enhance sound quality in recording and playback devices. The earliest designs featured rudimentary tone controls, which could boost or cut specific frequency ranges. As technology evolved, engineers developed more sophisticated equalizers, including graphic and parametric designs, allowing for precise adjustments across several frequency bands. With the advent of digital audio processing, equalization transcended the limitations of analog circuits, introducing dynamic and adaptive equalization methods. These advancements enable real-time analysis and adjustment of frequency content, significantly improving sound quality in diverse applications.

The Science Behind Equalization

To put equalization into a scientific context, consider the following fundamental concepts: 1. Frequencies and Wavelengths: The audible range for humans is approximately 20 Hz to 20 kHz. Understanding these ranges allows engineers to manipulate sound effectively. 2. Decibel Scale: Equalization adjustments are typically measured in decibels (dB), a logarithmic unit describing a ratio of power or intensity. For instance, a +3 dB increase corresponds to a doubling of power, while a -3 dB cut reduces the power by half. We can represent the relationship between amplitude and frequency response mathematically using the concept of transfer functions, defined as:

$$ H(s) = \frac{Y(s)}{X(s)} $$

Where: - $H(s)$ represents the transfer function, - $Y(s)$ is the output signal, - $X(s)$ is the input signal. This relationship allows engineers to predict how changes in equalization settings will affect the overall sound quality. In conclusion, equalization is not merely a tool for adjusting sound levels but a comprehensive technique that serves to enhance the listening experience. By mastering these techniques, audio engineers can ensure clarity, emotional depth, and spatial accuracy in sound reproduction, marking equalization as an indispensable aspect of audio engineering today.

Diagram Description: The diagram would illustrate the frequency response curve, showing how amplitude varies across the frequency spectrum for both linear phase and minimum phase filters. This visual representation would clarify the differences in behavior and application of these equalizers.

1.3 Types of Audio Equalizers

Audio equalizers are essential tools in the field of sound reproduction, enabling the adjustment of the balance between frequency components. Their capability to shape audio signals makes them invaluable in various applications, from professional music production to consumer-grade audio systems. Here, we delve into the primary types of audio equalizers, each with unique characteristics and practical applications.

Parametric Equalizers

Parametric equalizers are highly versatile and are designed to modify the amplitude of specific frequency bands. They allow the user to control three key parameters: frequency, gain, and bandwidth (Q factor). The Q factor determines the width of the affected frequency band, providing precision in sound shaping.

Mathematically, the transfer function of a parametric equalizer can be expressed as:

$$ H(f) = \frac{G}{1 + j \frac{f - f_0}{\Delta f}} $$

In this equation, G is the gain, f is the frequency of interest, f₀ is the center frequency, and Δf relates to the bandwidth. This level of control makes parametric equalizers invaluable for sound engineers during live shows and studio recordings, allowing for precise adjustments to counteract problematic frequencies or enhance desired tones.

Graphic Equalizers

Graphic equalizers differ from parametric equalizers in that they feature fixed frequency bands, each represented visually on a graph. The user can boost or cut the amplitude at these predetermined frequencies, typically spaced in octaves or fractions thereof.

A typical configuration would have bands centered at key frequencies such as 31.25 Hz, 62.5 Hz, 125 Hz, and so on, up to 16 kHz. This fixed bandwidth makes graphic equalizers user-friendly and quick to utilize, which is especially beneficial in live sound settings where fast adjustments are essential. The collective adjustments across each band combine to create a frequency response curve, which can be crucial for tonally adjusting music during live performances or recordings.

Shelving Equalizers

Shelving equalizers modify frequencies above or below a certain threshold, referred to as the shelf frequency. The gain can be increased or decreased for all frequencies above (high-shelf) or below (low-shelf) this threshold. They are particularly effective for overall tonal adjustments, such as brightening a track or adding warmth.

The mathematical representation for a shelving filter can be described as:

$$ H(f) = \frac{A + j \frac{f}{f_s}}{1 + j \frac{f}{b}} $$

Here, A is the gain at the shelf point, fₛ is the shelf frequency, and b indicates the cutoff slope. Common applications of shelving equalizers include mixing scenarios where a vital frequency range needs to be highlighted or de-emphasized, making them a staple in both studio and broadcasting applications.

All-Pass Equalizers

While not used for gain adjustments, all-pass equalizers are important for phase manipulation without altering the amplitude. They maintain a constant gain while shifting the phase of specific frequencies, which is critical in applications where phase coherence is vital, such as in multi-microphone setups or digital signal processing.

All-pass filters can be mathematically described as:

$$ H(f) = \frac{f - j \frac{f}{Q}}{1 + j \frac{f}{Q}} $$

Phase adjustments achieved through all-pass equalizers ensure that various sound sources are aligned, which can greatly influence the perception of sound in a mix, enhancing depth and clarity in audio playback.

Conclusion

Audio equalizers come in various forms, each suited to different needs in the audio processing chain. Understanding these nuances and their applications enables audio professionals to tailor their mixes more effectively. As technology advances, the integration of digital equalizers further broadens the capabilities of sound shaping, providing even greater control and precision.

Diagram Description: The diagram would depict the various types of audio equalizers, illustrating their operational principles and functions. It would clarify relationships between frequency, gain, and bandwidth for parametric equalizers, as well as the fixed band structure of graphic equalizers.

2. Resistors and Capacitors in Equalizer Circuits

2.1 Resistors and Capacitors in Equalizer Circuits

In audio equalizer circuits, resistors and capacitors play a crucial role in shaping frequency response and controlling audio signals. Understanding their functions and interactions is essential for designing effective equalization systems.

Fundamental Concepts of Resistors

Resistors are passive components that limit the flow of electric current. Their value, expressed in ohms (Ω), determines how much current will flow for a given voltage according to Ohm's Law:

$$ V = IR $$

where V is voltage, I is current, and R is resistance. In audio circuits, resistors can be used to attenuate (reduce) signal levels, create voltage dividers, and form part of complex network topologies for frequency manipulation.

The Role of Capacitors

Capacitors store electrical energy temporarily, releasing it when needed. Their ability to block direct current (DC) while allowing alternating current (AC) to pass makes them invaluable in filtering applications. The reactance of a capacitor (its resistance to AC) is frequency-dependent and is described by the formula:

$$ X_C = \frac{1}{2\pi f C} $$

where X_C is capacitive reactance, f is frequency, and C is capacitance in farads. This relationship implies that capacitors will allow more current to pass at higher frequencies, making them critical for frequency selection in equalizer circuits.

Combination: RC Filters in Equalizer Circuits

By pairing resistors and capacitors, engineers can create various filter configurations such as low-pass, high-pass, band-pass, and band-stop filters. Each configuration serves different purposes in audio processing:

Low-pass filters: Allow low frequencies to pass while attenuating higher frequencies. Often used to reduce unwanted noise in signal processing.
High-pass filters: Conversely, these filters let higher frequencies through while restricting lower ones, helpful in eliminating bass from audio streams.
Band-pass filters: These allow a specific range of frequencies to pass, which is particularly useful in modular synthesizers or specialized audio equalizers.

For instance, in a basic passive low-pass filter, employing a resistor R in series with a capacitor C forms the essential RC circuit. The cutoff frequency f_c of this filter can be calculated with:

$$ f_c = \frac{1}{2\pi RC} $$

Where R and C values can be adjusted to set the desired cutoff frequency, impacting the equalizer's response to audio signals significantly.

Applications in Audio Equalization

In practical applications, the combination of resistors and capacitors allows for the tailoring of audio signals to meet the specific needs of sound engineers and audiophiles. They are extensively found in:

DJ mixers, to enhance or reduce certain frequency ranges in live performances.
Home audio systems, to customize sound output according to room acoustics.
Professional recording studios, where precise control of frequency response is essential for achieving high-quality recordings.

In summary, the synergy between resistors and capacitors forms the backbone of audio equalizer design, facilitating control over audio frequencies and ensuring that electronic music production continues to evolve.

Conclusion

Understanding how resistors and capacitors interact within audio equalizers allows engineers and audio specialists to design circuits that can modify sound in nuanced ways. By mastering these components, practitioners can achieve their desired auditory outcomes, ranging from simple adjustments to complex signal processing tasks.

Diagram Description: The diagram would visually illustrate the RC filter configurations (low-pass, high-pass, band-pass, band-stop) by showing the arrangement of resistors and capacitors, as well as the signal flow through each configuration. This would clarify how different combinations affect frequency response.

2.2 Operational Amplifiers: Role and Function

Operational amplifiers (op-amps) form the backbone of audio equalizer circuits, playing a critical role in signal processing. While the basic operational amplifier can amplify voltage signals, it also possesses versatile properties that allow it to perform a wide range of operations including summation, integration, differentiation, and filtering. Understanding how these components function is essential for designing effective equalization circuits.

Understanding Operational Amplifiers

At their core, op-amps are direct current (DC) coupled high-gain voltage amplifiers designed to output a voltage that is a fraction of the difference between two input voltages. They are typically designated with two inputs: the inverting input (-) and the non-inverting input (+). The fundamental relationship governing an ideal op-amp is as follows:

$$ V_{out} = A \cdot (V^+ - V^-) $$

Where:
V_out = Output voltage
A = Open-loop gain (ideally infinite for an ideal op-amp)
V₊ = Voltage at the non-inverting terminal
V_- = Voltage at the inverting terminal

In practical circuits, though, op-amps are typically used in feedback configurations, which stabilize gain and dictate bandwidth. The closed-loop gain can be controlled by using resistors in the circuit, turning op-amps into highly configurable components in audio equalizers.

Key Characteristics of Operational Amplifiers

To employ op-amps effectively in audio processing, one must understand the essential characteristics governing their performance:

Input Impedance: Op-amps typically exhibit high input impedance (often megaohms), minimizing the loading effect on preceding stages in an audio chain.
Output Impedance: They also have low output impedance, allowing them to drive loads effectively.
Voltage Swing: The output voltage swings close to the power supply rails, allowing maximum output before clipping occurs.
Frequency Response: Understanding a specific op-amp’s gain-bandwidth product (GBP) is crucial, particularly in equalizer design where bandwidth affects the filter performance.

Application in Audio Equalizer Circuits

In audio equalizers, operational amplifiers are employed in various configurations—most commonly as active filters. These filters enable selective amplification or attenuation of specific frequency bands by adjusting the gain settings. For example:

Low Pass Filters: Allow frequencies below a certain threshold to pass while attenuating higher frequencies.
High Pass Filters: Function to allow higher frequencies and block lower frequencies.
Bass Boost/Cut Circuits: Specifically enhance or reduce frequencies in the bass range, typically employing a non-inverting amplifier configuration for gain control.

By cascading several op-amp stages, designers can create a sophisticated equalizer with multiple frequency bands tailored to the sound engineer's requirements.

Example Configuration: A Basic Equalizer

A simple graphic representation of a basic 3-band equalizer might depict three separate op-amps, each dedicated to a specific frequency range—low, mid, and high. Each would feature potentiometers to adjust gain, allowing real-time modifications to the audio signal.

This configuration exemplifies how multiple operational amplifiers can be effectively utilized in a single design to enhance audio quality in various applications, like live sound reinforcement or studio mixing.

In conclusion, operational amplifiers are indispensable in audio equalizer circuits, providing the necessary amplification and versatility to shape audio signals effectively.

Diagram Description: The diagram would illustrate the configuration of a basic 3-band equalizer, showing how the three operational amplifiers are connected to filter different frequency ranges. This would help visualize the relationships between the op-amps and their respective frequency bands, which could be complex when described only in text.

2.3 Potentiometers and Their Applications

Potentiometers are fundamental components in audio equalizer circuits, serving as variable resistors that allow for precise adjustments of audio signals. They operate on the principle of providing varying resistance thanks to their movable wiper contacts, which tap into a resistive element. Understanding the function and applications of potentiometers in audio circuits is crucial for optimizing audio performance and achieving desired tonal characteristics.

Understanding Potentiometers

A potentiometer typically consists of three terminals: two fixed terminals connected to a resistive element and a third movable terminal that adjusts the output voltage based on its position along the resistive path. This adjustable nature is what distinguishes potentiometers from fixed resistors, making them invaluable in applications that require tuning and calibration.

When deployed in audio circuits, potentiometers allow for control over volume, tone, and balance. For instance, in an equalization context, potentiometers can facilitate changes in specific frequency responses, effectively shaping the audio profile to meet listening preferences. This aspect of tuning audio systems is essential in professional audio engineering, enhancing sound quality based on environmental factors and listener preferences.

Mathematical Representation

To quantify the behavior of a potentiometer, we can express the output voltage—V_out—based on the input voltage—V_in—and the relative position of the wiper. Given the total resistance of the potentiometer, R_total, the output voltage can be expressed as:

$$ V_{out} = V_{in} \cdot \frac{R_w}{R_{total}} $$

Here, R_w represents the resistance between the wiper and one of the fixed terminals. As the wiper moves, R_w changes, thus varying the output voltage. In an audio equalizer circuit, this variability allows for real-time adjustments to sound frequency levels.

Real-World Applications

The practical applications of potentiometers in audio equalizers extend to both consumer electronics and professional sound systems. In home stereos, users can manipulate treble and bass settings through potentiometers, tailoring sound quality to individual tastes. In contrast, mixing consoles in recording studios utilize multi-channel potentiometers for precise control over channel levels, enabling sound engineers to create balanced mixes conducive to professional audio production.

Furthermore, the integration of digital potentiometers in modern audio equipment has revolutionized how we interact with these components. Digital potentiometers, controlled by microcontrollers, offer enhanced precision and automation for equalization tasks. This technology exemplifies the movement towards the digitalization of audio technologies, providing stability and ease of use compared to their analog counterparts.

In conclusion, understanding the role of potentiometers in audio equalizers is critical for any advanced-level reader seeking to design or optimize audio systems. Their capacity to offer fine-tuned adjustments makes them essential in achieving desired audio characteristics tailored to user preferences and the acoustic environment.

Diagram Description: The diagram would illustrate the configuration of a potentiometer, highlighting its three terminals and the resistive element, as well as depicting how the wiper position affects the output voltage. This clarity aids in visualizing the relationship between the components and the output voltage formula provided.

3. Passive Equalizer Design Principles

3.1 Passive Equalizer Design Principles

Audio equalizers play a pivotal role in shaping the sound characteristics of a system. At the core of equalization lies the ability to manipulate various frequency bands, enhancing or attenuating them based on the requirements of the listening environment or personal preferences. This subsection focuses on passive equalizer design principles, which provide a fundamental approach using passive components like resistors, capacitors, and inductors.

Understanding Passive Equalizers

Passive equalizers are circuits that rely solely on passive components, without the need for amplification. These designs utilize filters to divide the audio spectrum into separate frequency bands. As the name suggests, they do not add power; rather, they redistribute the power of existing signals. The primary components, namely resistors (R), capacitors (C), and inductors (L), work together to create frequency-selective responses.

One of the fundamental principles in designing passive equalizers relies on the understanding of how capacitors and inductors behave in response to changes in frequency. Capacitors store energy in an electric field and exhibit a frequency-dependent impedance that decreases with increasing frequency. Conversely, inductors store energy in a magnetic field, presenting an impedance that increases with frequency. This distinct behavior constitutes the cornerstone of RC and RL filters used in equalization.

Types of Filters in Passive Equalizers

Passive equalizers typically deploy a combination of high-pass, low-pass, and band-pass filters. Each type serves a different purpose:

High-pass filters: Allow frequencies above a certain cutoff frequency to pass while attenuating lower frequencies.
Low-pass filters: Opposite of high-pass; they permit low frequencies while blocking higher frequencies.
Band-pass filters: Combine the characteristics of both to allow a specific band of frequencies, making them particularly useful for graphic and parametric equalizers.

Filter Design Equations

To design a filter for a passive equalizer, it's essential to derive the appropriate equations. Let's explore the transfer function of a simple low-pass filter formed by a resistor and capacitor (RC). The configuration is as follows:

For an RC low-pass filter, the transfer function $ H(s) $ can be expressed in the s-domain as:

$$ H(s) = \frac{1}{1 + sRC} $$

Here, $ s $ is the complex frequency variable $ s = j\omega $, where $ j $ is the imaginary unit and $ \omega $ is the angular frequency. The -3dB cutoff frequency ($ f_c $) of this filter is crucial for identifying the transition point where the output power falls to half of the input power.

The cutoff frequency is obtained using the formula:

$$ f_c = \frac{1}{2\pi RC} $$

Adjusting the values of $ R $ and $ C $ allows designers to move the cutoff frequency, catering to specific audio adjustment needs. In practical applications, multiple RC stages can be cascaded to create more complex filters.

Applications of Passive Equalizers

Passive equalizers are widely employed in various audio systems, including:

Analog synthesizers, where the sound sculpting capabilities are essential for sound design.
High-fidelity audio systems, helping audiophiles optimize their listening environments.
Broadcast equipment, ensuring signal quality adheres to transmission standards.

The practical simplicity, reliability, and cost-effectiveness of passive equalizers make them favored in both consumer and professional audio applications. Furthermore, as they do not require power, they are less prone to distortion and noise, which can be critical in preserving audio quality.

Understanding the principles of passive equalizer design provides a solid foundation for exploring more complex active designs that incorporate operational amplifiers and other active components, enabling even greater flexibility in sound modification.

Diagram Description: The diagram would illustrate the configuration of an RC low-pass filter, including the relationship between the resistor and capacitor. It would visually depict the frequency response curve, highlighting the -3dB cutoff frequency.

3.2 Active Equalizer Circuit Design

Active equalizer circuits represent a sophisticated means of audio signal manipulation, leveraging operational amplifiers and feedback networks to deliver precise gain adjustments across different frequency bands. Unlike passive equalizers, which can only attenuate frequencies, active equalizers facilitate both amplification and attenuation, making them far more versatile for audio applications.

At the core of an active equalizer is usually an operational amplifier (op-amp), a critical element that allows for various configurations to achieve the desired frequency response. The op-amp serves as a voltage-controlled gain stage, where the gain can be determined by external resistors and capacitors. Furthermore, feedback mechanisms enable distinct bandpass behaviors at specific frequencies—an essential feature when refining audio performances.

Basic Design Principles

The design of an active equalizer circuit typically involves several stages, with each stage tailored to adjust specific frequency bands. The most common architectures include:

Low-Shelf Filters: Adjusts gain for frequencies below a designated cutoff frequency.
High-Shelf Filters: Adjusts gain for frequencies above a specific cutoff.
Bandpass Filters: Isolates and modifies a specific frequency range.

Each filter configuration generally involves a combination of resistors (R) and capacitors (C) in a feedback loop around an op-amp. Selecting appropriate values for these components directly influences the circuit's frequency response, bandwidth, and gain characteristics. For example, in a low-pass configuration, as illustrated in the subsequent mathematical derivation, the cutoff frequency can be established using the formula:

$$ f_c = \frac{1}{2\pi RC} $$

Where:

f_c: Cutoff frequency
R: Resistance value in ohms
C: Capacitance value in farads

Gain Manipulation Using Feedback

To manipulate gain at specific frequencies effectively, we need to leverage both positive and negative feedback in our circuit design. An essential feature of negative feedback is that it stabilizes gain and minimizes distortion, which is critical in audio applications.

Consider an active equalizer designed with multiple op-amps, each configured as a non-inverting amplifier for greater flexibility. The voltage gain A can be expressed as follows:

$$ A = 1 + \frac{R_f}{R_g} $$

Where:

R_f: Feedback resistor
R_g: Grounded resistor connected to the inverting input

The configuration and values selected for these resistors directly influence the amount of gain applied to each filter stage and thus, the active equalizer's overall performance.

Practical Considerations and Applications

In modern audio equipment, active equalizers find prevalent applications in mixing consoles, sound reinforcement systems, and home audio setups. They allow sound engineers and audiophiles to tailor the output more aptly to their preferences or acoustic environments. One practical case is during live performances where feedback suppression and equalization adjustments are crucial for delivering high-quality audio without distortion.

Furthermore, implementing digital signal processing (DSP) techniques alongside active equalization has become increasingly popular, allowing for further refinement and flexibility in audio frequencies through software-based means.

Ultimately, the design of active equalizer circuits combines theoretical principles with practical applications, highlighting the importance of precise control over audio frequencies in diverse environments. As audio technology advances, these designs will continue to evolve, supporting ever more refined auditory experiences.

Diagram Description: The diagram would visually represent the configuration of an active equalizer circuit, highlighting the relationships between the op-amps, resistors, and capacitors in various filter configurations such as low-shelf, high-shelf, and bandpass filters.

3.3 Frequency Response and Tuning Techniques

Understanding Frequency Response

In the context of audio equalizer circuits, frequency response describes how an equalizer processes different frequencies in an audio signal. It is a critical concept in both design and application, influencing sound quality and overall performance. More formally, frequency response is defined as the steady-state response of an electronic circuit to a sinusoidal input signal over a range of frequencies. This relationship is usually illustrated graphically, showcasing the amplitude of the output signal as a function of frequency, often represented in decibels (dB). The Bode plot is a common method used to visualize the frequency response of systems, consisting of two plots: the magnitude plot (in dB) and the phase plot (in degrees). Each plot provides essential insights into how the equalizer circuit behaves at various frequencies, crucial for understanding tuning techniques and adjustments.

Tuning Techniques in Audio Equalizers

The tuning of audio equalizers often involves manipulating various circuit components to achieve desired frequency responses. The main goals include compensating for deficiencies in sound reproduction and tailoring the audio output to the preferences of the listener. Below are some key tuning techniques:

Passive Equalization: Implementing resistors and capacitors in a specific configuration allows for attenuation and boosting of particular frequency bands. Passive filters are generally simpler but can introduce losses that need compensation.
Active Equalization: Active circuits utilize operational amplifiers (op-amps) to provide gain and create more complex filter responses. They are capable of boosting signals without inducing loss, making them a popular choice in professional audio applications.
Digital Equalization: Utilizing digital signal processing (DSP) allows for high precision and flexibility. Digital equalizers can provide adaptive tuning based on real-time analysis of the audio input, enabling filters to change dynamically to suit the acoustic environment.
Feedback Mechanisms: Implementing feedback loops within circuits helps stabilize the gain and improve the performance of equalizers by reducing noise and distortion. In some designs, feedback can semi-automatically adjust based on the audio signal itself.

Mathematical Representations

For engineers and researchers, analytical approaches are crucial for designing effective audio equalizers. The transfer function is an essential tool that describes the relationship between the input and output signals in the frequency domain. For a simple first-order low-pass filter, the transfer function can be expressed as: $$ H(s) = \frac{1}{1 + sRC} $$ Where: - $ H(s) $ = Transfer function - $ R $ = Resistance (Ohms) - $ C $ = Capacitance (Farads) - $ s $ = Complex frequency By analyzing the frequency response derived from the transfer function, the cutoff frequency ($ f_c $) can be computed as: $$ f_c = \frac{1}{2\pi RC} $$ This equation crucially dictates where the signal will start being attenuated, defining the operational bandwidth of the equalizer section incorporated in the circuit. In practice, bidirectional adjustments can pave the way to fine-tuning a given frequency specific to environmental considerations. By leveraging both passive and active components, one can achieve a tailored response curve that fits real-world audio applications. In summary, understanding the interplay between frequency response and different tuning techniques empowers engineers to design efficient audio equalizers that meet diverse auditory demands across applications ranging from personal music systems to professional sound reinforcement environments.

Diagram Description: A diagram could effectively illustrate the Bode plot, showing the magnitude and phase response of the equalizer circuit across various frequencies, which is vital for understanding tuning techniques. Additionally, the diagram can visualize both active and passive tuning component configurations in a clear manner.

4. Graphic Equalizer Circuits

4.1 Graphic Equalizer Circuits

Graphic equalizers are essential tools in audio signal processing, offering precise control over sound frequencies. They consist of a series of filters, each targeting a specific frequency band, which allows users to boost or cut frequencies to tailor the audio output for various environments or preferences. This subsection will explore the underlying principles of graphic equalizer circuits, their components, and practical implementations in both studio and live sound settings.

Fundamentals of Graphic Equalization

A graphic equalizer typically divides the audio spectrum into a series of bands—commonly 10, 15, or 31 bands—each centered around a specific frequency. These frequency bands allow audio engineers to manipulate sound more intuitively. Unlike parametric equalizers, which provide adjustable Q factors and gain, graphic equalizers offer a fixed Q factor for each band, simplifying the equalization process and making it easier to visualize adjustments.

Filter Types and Their Configuration

The fundamental building blocks of graphic equalizers are band-pass filters. Each band-pass filter allows a particular range of frequencies to pass while attenuating all others. The most common types of filters used are:

Low-Pass Filters: These enable frequencies below a certain cutoff frequency while attenuating higher frequencies.
High-Pass Filters: These do the opposite, allowing frequencies above the cutoff to pass and attenuating the lower frequencies.
Band-Pass Filters: These combine both low and high-pass attributes, allowing only a specific frequency range to be transmitted.

The filters are often configured using operational amplifiers (op-amps) due to their high input impedance and low output impedance, making them ideal for audio applications.

Mathematical Modeling of a Graphic Equalizer

For each frequency band i, the transfer function can be mathematically represented as:

$$ H_i(s) = \frac{K_i \cdot \omega}{s + \omega} $$

Where:

H_i(s): Transfer function of the i-th band
K_i: Gain factor for the i-th band
ω: Angular frequency at the i-th band center frequency
s: Complex frequency variable in the Laplace domain

To design a graphic equalizer with N bands, the overall transfer function H(s) can be obtained by multiplying the individual transfer functions:

$$ H(s) = \prod_{i=1}^{N} H_i(s) $$

This equation illustrates that the overall response is a product of the individual responses of all band-pass filters implemented in the circuit.

Practical Example: Implementing a 10-Band Graphic Equalizer

In a practical design, the values for K_i can be set depending on the desired boost (K_i > 1) or cut (K_i < 1) for each frequency band. Typically, each filter is constructed using a resistor-capacitor (RC) network paired with op-amps. The selection of resistor and capacitor values determines the cutoff frequencies and the bandwidth of each filter, emphasizing the importance of precise component selection. A typical layout includes:

Operational amplifiers (e.g., TL072) for the signal processing.
Resistors and capacitors in specific configurations to set cutoff frequencies accurately.
Slider potentiometers for user-adjustable band gains.

In audio engineering applications, graphic equalizers are vital for optimizing audio signals in various environments. For instance, their use can significantly improve sound in performance venues, allowing sound engineers to compensate for room acoustics effectively.

Conclusion

Graphic equalizer circuits combine mathematical elegance with practical necessity, enabling users to shape sound perceptively. Their application spans professional audio, home theater systems, and even personal listening devices. A deeper understanding of the underlying principles enhances the ability of audio professionals to apply these tools effectively, ensuring superior sound quality in diverse settings.

Diagram Description: A diagram would visually represent the configuration of the band-pass filters within a graphic equalizer circuit, showing how frequency bands are handled and how op-amps interface with resistors and capacitors. This will clarify the functionality and interconnections that text alone cannot fully convey.

4.1 Graphic Equalizer Circuits

Fundamentals of Graphic Equalization

Filter Types and Their Configuration

Low-Pass Filters: These enable frequencies below a certain cutoff frequency while attenuating higher frequencies.
High-Pass Filters: These do the opposite, allowing frequencies above the cutoff to pass and attenuating the lower frequencies.
Band-Pass Filters: These combine both low and high-pass attributes, allowing only a specific frequency range to be transmitted.

The filters are often configured using operational amplifiers (op-amps) due to their high input impedance and low output impedance, making them ideal for audio applications.

Mathematical Modeling of a Graphic Equalizer

For each frequency band i, the transfer function can be mathematically represented as:

$$ H_i(s) = \frac{K_i \cdot \omega}{s + \omega} $$

Where:

H_i(s): Transfer function of the i-th band
K_i: Gain factor for the i-th band
ω: Angular frequency at the i-th band center frequency
s: Complex frequency variable in the Laplace domain

To design a graphic equalizer with N bands, the overall transfer function H(s) can be obtained by multiplying the individual transfer functions:

$$ H(s) = \prod_{i=1}^{N} H_i(s) $$

This equation illustrates that the overall response is a product of the individual responses of all band-pass filters implemented in the circuit.

Practical Example: Implementing a 10-Band Graphic Equalizer

Operational amplifiers (e.g., TL072) for the signal processing.
Resistors and capacitors in specific configurations to set cutoff frequencies accurately.
Slider potentiometers for user-adjustable band gains.

Conclusion

4.2 Parametric Equalizer Circuits

A parametric equalizer is a versatile tool widely utilized in audio processing, allowing precise modifications to a sound's frequency content. Unlike simple equalizers that apply fixed gain adjustments at set frequencies, parametric equalizers provide audio engineers with the ability to dynamically control not only the gain but also the center frequency and bandwidth of each filter. This capability is particularly beneficial when fine-tuning audio signals for different environments or correcting specific issues in recordings.

Core Principles of Parametric Equalization

The operation of a parametric equalizer hinges upon the principle of filtering, specifically using bandpass filters. Each filter can be characterized by three primary parameters:

Center frequency (f0): The frequency at which the filter will have its maximum gain.
Gain (G): The amount of amplification applied to the audio signal at the center frequency.
Bandwidth (BW): Often expressed in terms of quality factor (Q), which defines how wide or narrow the filter's effect will be around the center frequency.

By varying these parameters, users can emphasize or attenuate specific frequency ranges within the audio spectrum, ranging from low bass notes to high-frequency treble sounds. This flexibility allows for a tailored audio output that meets the needs of different listening environments, such as live performances, studio recordings, or personal listening setups.

Mathematical Representation

To understand how a parametric equalizer modifies an audio signal, we can use the following equations derived from the standard second-order (biquad) filter model. The transfer function $H(s)$ of a bandpass filter can be expressed as:

$$ H(s) = \frac{G \cdot \frac{s}{\omega_0}}{1 + \frac{s}{Q\omega_0} + \left( \frac{s}{\omega_0} \right)^2} $$

In this equation, $s$ is the complex frequency variable, $G$ is the gain at the center frequency, $ \omega_0 = 2\pi f_0$ is the angular frequency, and $Q$ is the quality factor which defines the bandwidth.

To achieve a desired response, we must select appropriate values for $G$, $f_0$, and $Q$. The quality factor $Q$ can be determined based on the desired bandwidth $BW$ using the formula:

$$ Q = \frac{f_0}{BW} $$

This relationship emphasizes the trade-offs between gain and bandwidth: a higher $Q$ results in a narrower bandwidth, hence more precise manipulation of specific frequencies, but may also lead to an increased risk of introducing noise or unwanted resonances.

Implementation of a Parametric Equalizer

In a practical application, parametric equalizers are often implemented using operational amplifiers (op-amps) configured in various filter arrangements. A common choice is to use multiple cascading stages of second-order filters, which enables the design of flexible multi-band equalizers. A typical design may utilize digitally controlled potentiometers to adjust gain and bandwidth dynamically, thereby allowing real-time manipulation during performance or recording sessions.

The development of digital parametric equalizers has further enhanced their applicability in modern audio processing. Digital signal processing (DSP) allows for advanced algorithms that can automatically analyze an audio signal and suggest optimal filter settings based on predefined criteria, making equalization both precise and intuitive for sound engineers.

Real-World Applications

Parametric equalizers find utility in various environments, from sophisticated recording studios to live sound systems. They are instrumental for:

Room correction: By identifying problematic frequencies in a room's acoustics, engineers can employ parametric equalizers to compensate for the acoustic flaws of the environment.
Musical composition: Artists can creatively mold their sound by accentuating particular frequencies that enhance the artistic intention behind their work.
Broadcasting: Ensuring clarity and intelligibility in spoken word applications, such as news reporting or public speaking, relies heavily on careful frequency adjustments.

In essence, the adaptability and precision of parametric equalizers make them indispensable tools for sound manipulation across diverse audio applications.

Diagram Description: The diagram would illustrate the operation of a parametric equalizer with its key components such as the bandpass filter, center frequency, gain, and bandwidth. This visualization aids in grasping the interactions between these parameters and their impact on the audio signal.

4.2 Parametric Equalizer Circuits

Core Principles of Parametric Equalization

The operation of a parametric equalizer hinges upon the principle of filtering, specifically using bandpass filters. Each filter can be characterized by three primary parameters:

Center frequency (f0): The frequency at which the filter will have its maximum gain.
Gain (G): The amount of amplification applied to the audio signal at the center frequency.
Bandwidth (BW): Often expressed in terms of quality factor (Q), which defines how wide or narrow the filter's effect will be around the center frequency.

Mathematical Representation

$$ H(s) = \frac{G \cdot \frac{s}{\omega_0}}{1 + \frac{s}{Q\omega_0} + \left( \frac{s}{\omega_0} \right)^2} $$

To achieve a desired response, we must select appropriate values for $G$, $f_0$, and $Q$. The quality factor $Q$ can be determined based on the desired bandwidth $BW$ using the formula:

$$ Q = \frac{f_0}{BW} $$

Implementation of a Parametric Equalizer

Real-World Applications

Parametric equalizers find utility in various environments, from sophisticated recording studios to live sound systems. They are instrumental for:

Room correction: By identifying problematic frequencies in a room's acoustics, engineers can employ parametric equalizers to compensate for the acoustic flaws of the environment.
Musical composition: Artists can creatively mold their sound by accentuating particular frequencies that enhance the artistic intention behind their work.
Broadcasting: Ensuring clarity and intelligibility in spoken word applications, such as news reporting or public speaking, relies heavily on careful frequency adjustments.

In essence, the adaptability and precision of parametric equalizers make them indispensable tools for sound manipulation across diverse audio applications.

4.3 Shelving Equalizer Circuits

Shelving equalizer circuits play a crucial role in audio signal processing, allowing engineers to enhance or attenuate specific frequency ranges effectively. These circuits are characterized by their ability to adjust the gain of frequencies above or below a defined cutoff frequency, thus providing a balanced and controlled tonal adjustment that can enhance music clarity and listening experience. In this section, we will delve into the principles of designing shelving equalizers, practical applications, and how they differ from other types of equalizers, such as peaking filters.

Understanding Shelving Filters

A shelving equalizer can be conceptualized as consisting of two distinct types of filters in one circuit: a high shelving filter and a low shelving filter. The basic idea is to create a circuit that significantly boosts or cuts the amplitude of audio signals beyond a certain frequency threshold.

The transfer function of a shelving filter can be derived using the principles of circuit theory combined with frequency response characteristics.

Mathematical Derivation

To derive the transfer function for a shelving equalizer, consider the basic components: capacitors and resistors that form the filter characteristics. For a simple high-shelving filter, the transfer function $ H(s) $ can be modeled as:

$$ H(s) = \frac{K + \frac{s}{\omega_c}}{1 + \frac{s}{\omega_0}} $$

In this equation:

K represents the gain above the cutoff frequency.
$\omega_c$ is the angular cutoff frequency where gain begins to change.
$\omega_0$ defines the overall resonance frequency.

For a low-shelving filter, the transfer function changes slightly, focusing on reducing signal amplitude for frequencies below a specified point. The process of determining the exact values for $ K, \omega_c, $ and $ \omega_0 $ requires a thorough understanding of the desired audio characteristics as well as real-world testing and tuning.

Practical Implementation

In real-world applications, shelving equalizers are frequently utilized in various audio devices, from simple home audio systems to professional audio mixing consoles. As they offer a straightforward way to adjust tonal balance, they are favored in scenarios where broad adjustments are required, such as:

Live sound reinforcement — where quick adjustments may be necessary.
Music production — allowing producers to sculpt sounds within a track.
Broadcasting — enhancing speech intelligibility by emphasizing certain frequency ranges.

Comparative Analysis with Peaking Filters

It's beneficial to contrast shelving equalizers with peaking filters. While both can adjust specific frequency ranges, peaking filters allow for a more surgical level of control, typically targeting narrower bands. This makes shelving equalizers more suitable for applications requiring broader, more general tonal adjustments, while peaking filters excel in precision tasks like correcting tonal imbalances in individual tracks. The choice between the two depends greatly on the application context and specific sound design objectives.

Conclusion

Shelving equalizer circuits are invaluable tools in audio engineering, providing users with the means to enhance their sound systems and achieve an optimal audio experience. Mastering the design and application of these circuits can facilitate improved audio quality across a range of devices, from consumer electronics to professional studio equipment. Understanding their principles and practical applications will equip professionals with the necessary skills to manipulate audio signals effectively.

Diagram Description: The diagram would illustrate the high shelving and low shelving filter characteristics in terms of their frequency response, showing how gain is adjusted above and below the cutoff frequency. This visual representation will clarify the differences in application and design principles between shelving equalizers and peaking filters.

4.3 Shelving Equalizer Circuits

Understanding Shelving Filters

The transfer function of a shelving filter can be derived using the principles of circuit theory combined with frequency response characteristics.

Mathematical Derivation

$$ H(s) = \frac{K + \frac{s}{\omega_c}}{1 + \frac{s}{\omega_0}} $$

In this equation:

K represents the gain above the cutoff frequency.
$\omega_c$ is the angular cutoff frequency where gain begins to change.
$\omega_0$ defines the overall resonance frequency.

Practical Implementation

Live sound reinforcement — where quick adjustments may be necessary.
Music production — allowing producers to sculpt sounds within a track.
Broadcasting — enhancing speech intelligibility by emphasizing certain frequency ranges.

Comparative Analysis with Peaking Filters

Conclusion

5. Studio Mixing and Mastering

5.1 Studio Mixing and Mastering

In audio production, mixing and mastering are critical processes that ensure the final sound output is polished, balanced, and ready for distribution. Audio equalizer circuits play a pivotal role in both these steps, allowing for precise control over the audio frequencies. Understanding how to effectively utilize these circuits can significantly enhance the quality of your audio projects.

Mixing: Balancing Frequencies

During the mixing phase, individual audio tracks are combined to create a cohesive sound. This involves adjusting levels, panning, and applying effects such as compression and reverb. The audio equalizer comes into play as a tool for frequency shaping, allowing sound engineers to enhance or attenuate specific frequency bands.

Mixing engineers often utilize parametric equalizers for their versatility. A typical parametric equalizer allows for adjustments to the center frequency, gain, and bandwidth (or Q factor). Understanding the relationship between these parameters is essential for effective mixing:

Center Frequency: This determines which frequency will be affected by the EQ adjustments. It defines the peak of the equalizer's curve.
Gain: This controls the amplitude of the specified frequency range. Positive gain boosts frequencies, while negative gain cuts them.
Bandwidth/Q Factor: This parameter determines how wide or narrow the affected frequency range is. A higher Q factor means a narrower bandwidth.

By employing specific EQ settings tailored to each track's characteristics, engineers can eliminate frequency conflicts, making room for each instrument in the mix. For example, cutting frequencies around 300 Hz may help reduce muddiness, while boosting around 2.5 kHz can enhance vocal presence.

Mastering: The Final Touch

Once mixing is complete, the next step is mastering. This involves preparing the final mix for distribution by optimizing the overall sound, ensuring consistency across tracks, and making it compatible with different playback systems. Equalizers in mastering are usually used more subtly compared to mixing.

The aim in mastering with EQ is to refine and enhance the overall mix without introducing new elements. The common practices include:

Low-End Tightening: Using low-shelf filters to tighten the low-end frequencies and eliminate any unnecessary sub-bass that could muddy the mix.
Midrange Clarity: Gentle boosts in the 1-2 kHz range can enhance clarity, making vocals and lead instruments more prominent in the mix.
Air and Space: High-shelf filters can add a sense of airiness by boosting frequencies above 10 kHz, giving the final track a polished, professional sound.

Practical Application: Real-World Scenarios

In professional studios, advanced equalizer circuits often utilize analog processing to impart warmth and character to the audio. Classic models like the API 550A and the Neve 1073 are revered for their unique sonic qualities, often sought after in the final stages of mixing and mastering.

The use of digital audio workstations (DAWs) has opened up additional realms of equalization techniques with digital parametric and graphic equalizers. They allow engineers to visualize the frequency spectrum, making it easier to make informed decisions regarding frequency adjustments.

Through meticulous mixing and mastering, enhanced by the effective application of audio equalizer circuits, audio engineers can produce high-quality recordings that stand out in competitive audio landscapes. This understanding converges both artistry and engineering, culminating in a polished final product that resonates with listeners.

Diagram Description: The diagram would visually represent the relationship between the center frequency, gain, and bandwidth/Q factor of a parametric equalizer. This would clarify how these parameters interact and affect sound manipulation in mixing and mastering.

5.1 Studio Mixing and Mastering

Mixing: Balancing Frequencies

Center Frequency: This determines which frequency will be affected by the EQ adjustments. It defines the peak of the equalizer's curve.
Gain: This controls the amplitude of the specified frequency range. Positive gain boosts frequencies, while negative gain cuts them.
Bandwidth/Q Factor: This parameter determines how wide or narrow the affected frequency range is. A higher Q factor means a narrower bandwidth.

Mastering: The Final Touch

The aim in mastering with EQ is to refine and enhance the overall mix without introducing new elements. The common practices include:

Low-End Tightening: Using low-shelf filters to tighten the low-end frequencies and eliminate any unnecessary sub-bass that could muddy the mix.
Midrange Clarity: Gentle boosts in the 1-2 kHz range can enhance clarity, making vocals and lead instruments more prominent in the mix.
Air and Space: High-shelf filters can add a sense of airiness by boosting frequencies above 10 kHz, giving the final track a polished, professional sound.

Practical Application: Real-World Scenarios

5.2 Live Sound Reinforcement

In the realm of audio engineering, particularly concerning live sound reinforcement, equalizers play a pivotal role in shaping the auditory experience. This subsection delves into the intricacies of equalizer circuits, examining how they can be effectively utilized to enhance live sound experiences. With a focus on practical application and real-world scenarios, we will explore the technical nuances that govern the optimal use of audio equalizers in live settings.

Understanding the Role of Equalizers in Live Sound

Equalizers are essential tools in live sound reinforcement, responsible for adjusting the balance between frequency components within an audio signal. They allow sound technicians to tailor audio outputs to fit specific environments, compensate for acoustic anomalies, and ensure clarity and balance across various sound sources.

Typically, a live sound equalizer operates by using a series of filters to manipulate gain at specific frequency bands. These filters can take on various forms, including low-pass, high-pass, band-pass, and notch filters, each serving distinct functions in sound shaping. The most common types of equalizers used in live sound reinforcement include:

Graphic Equalizers: These consist of multiple fixed-band filters with sliders for adjusting the amplitude of each band. They provide a visual representation of the equalization adjustments.
Parametric Equalizers: These allow for more precise control, providing adjustable bandwidth (Q) and center frequency selections, making them ideal for surgical corrections.

Practical Applications and Techniques

In practice, sound engineers utilize equalizers to address various challenges in live settings. For instance, a common issue faced in concert venues is feedback, which can be mitigated by carefully applying a notch filter at the frequency where feedback occurs. This process involves:

Identifying the problematic frequency through listening and analysis tools.
Setting a narrow bandwidth on a parametric equalizer to isolate that frequency.
Reducing the gain to suppress feedback while maintaining overall sound quality.

Additionally, equalizers can be used for artistic effects by boosting certain frequency ranges to enhance the vocal presence or by cutting lower frequencies to reduce muddiness in a mix. The combination of these adjustments contributes significantly to the overall sound quality and audience experience.

Implementing Equalizers in Live Sound Systems

When integrating an equalizer into a live sound system, there are several considerations that must be taken into account:

System Configuration: Understanding the configuration of the audio system (i.e., frontend and backend signal flow) is crucial for effective equalizer placement. An equalizer can be inserted into the signal path of individual channels, groups, or the master output.
Room Acoustics: Every venue has unique acoustics that dictate the necessary adjustments on the equalizer. Pre-show sound checks to analyze room response can help in setting the initial parameters.
Real-time Adjustments: During live performances, constant monitoring is essential. Engineers may need to make real-time adjustments to accommodate changes in performance dynamics and audience interaction.

Conclusion

As the sound environment evolves, so too must the strategies employed by sound engineers. An effective equalizer circuit can dramatically shape the live audio experience, ensuring clarity, balance, and musical integrity. The responsive use of equalization techniques empowers sound professionals to deliver exceptional auditory experiences in various live settings, from intimate venues to vast arenas.

Diagram Description: The diagram would illustrate the signal flow in live sound reinforcement, showing how an equalizer fits into the audio system and the relationship between the various components such as microphones, speakers, and signal paths. This visual representation would clarify the integration and placement of equalizers in different configurations.

5.2 Live Sound Reinforcement

Understanding the Role of Equalizers in Live Sound

Graphic Equalizers: These consist of multiple fixed-band filters with sliders for adjusting the amplitude of each band. They provide a visual representation of the equalization adjustments.
Parametric Equalizers: These allow for more precise control, providing adjustable bandwidth (Q) and center frequency selections, making them ideal for surgical corrections.

Practical Applications and Techniques

Identifying the problematic frequency through listening and analysis tools.
Setting a narrow bandwidth on a parametric equalizer to isolate that frequency.
Reducing the gain to suppress feedback while maintaining overall sound quality.

Implementing Equalizers in Live Sound Systems

When integrating an equalizer into a live sound system, there are several considerations that must be taken into account:

System Configuration: Understanding the configuration of the audio system (i.e., frontend and backend signal flow) is crucial for effective equalizer placement. An equalizer can be inserted into the signal path of individual channels, groups, or the master output.
Room Acoustics: Every venue has unique acoustics that dictate the necessary adjustments on the equalizer. Pre-show sound checks to analyze room response can help in setting the initial parameters.
Real-time Adjustments: During live performances, constant monitoring is essential. Engineers may need to make real-time adjustments to accommodate changes in performance dynamics and audience interaction.

Conclusion

5.3 Home Audio Systems

Audio equalizers play a vital role in enhancing sound quality across various platforms, particularly in home audio systems. These systems are comprised of multiple components, including speakers, amplifiers, and audio sources, which collectively ensure an immersive listening experience. To tailor listening preferences, equalizer circuits allow precise adjustments to the audio frequency spectrum, which can notably improve clarity and reproduce nuances of music and sound.

When we delve into the architecture of home audio systems, the role of the equalizer becomes significant. A standard home audio setup typically includes a source device (like a CD player, streaming device, or turntable), an amplifier, and a speaker system. The equalizer is often integrated into the amplifier or responsible for preamplifying the audio signal before it reaches the main amplifier stage.

Types of Equalizers in Home Audio Systems

Audio equalizers can be classified primarily into two categories: graphic equalizers and parametric equalizers.

Graphic Equalizers: These feature a fixed number of bands (usually ranging from 5 to 31) corresponding to specific frequency ranges. Users can visually manipulate sliders that represent these bands, effectively shaping the audio signal to meet their preferences. The straightforward design makes them popular for consumer audio systems.
Parametric Equalizers: More sophisticated than graphic equalizers, parametric equalizers allow users to adjust not only the amplitude of specific frequencies but also the frequency center and bandwidth (or Q factor). This flexibility makes parametric equalizers especially useful in professional audio settings for tailored sound shaping.

The Role of Digital Signal Processing (DSP)

With advancements in technology, many modern home audio systems utilize Digital Signal Processing (DSP) to achieve audio manipulation. DSPs perform equalization tasks via software algorithms, enabling complex filters and effects without the need for extensive analog circuitry. This digital approach provides further advantages, such as:

Precision: DSP can fine-tune audio signals with remarkable accuracy, surpassing the capabilities of analog equalizers.
Customization: Users can create highly personalized sound profiles for different genres or listening environments, adjusting parameters dynamically for optimal experience.
Integration: DSP effortlessly integrates with various audio formats and electronic devices, making it suitable for the connected home environment.

Moreover, DSP-based equalizers can implement adaptive equalization techniques, which analyze the acoustics of a room in real-time and adjust the audio output accordingly. This intelligent feature enhances overall audio fidelity and compensates for unwanted resonances that might occur due to room geometry and materials.

Practical Considerations in Home Audio Design

While selecting equalizers for home audio systems, one must consider several factors:

Room Acoustics: The physical characteristics of a room, including its size and material, influence sound propagation. Understanding these aspects helps design a system that effectively compensates for such variances.
Listener Preferences: Ultimately, the effectiveness of an equalizer is subjective, relying heavily on individual sound preferences. A flat frequency response may appeal to some listeners, while others may prefer a more colored sound profile.
Signal Chain Integrity: Protecting the audio signal from degradation throughout the chain—from source to speaker—is crucial. An equalizer introduced into the signal path should not compromise audio quality, making high-fidelity components essential.

In conclusion, audio equalizer circuits, especially in home audio systems, provide a necessary interface between raw sound and tailored listening experiences. Whether utilizing analog or digital methods, the ability to manipulate frequency response fundamentally enhances listener satisfaction, making knowledge of these systems essential for both sound engineers and enthusiasts alike.

Diagram Description: The diagram would show the block diagram of a typical home audio system, illustrating the order and connections between the source device, equalizer, amplifier, and speakers. This visual representation would clarify the signal flow and the role of the equalizer within the overall system architecture.

5.3 Home Audio Systems

Types of Equalizers in Home Audio Systems

Audio equalizers can be classified primarily into two categories: graphic equalizers and parametric equalizers.

Graphic Equalizers: These feature a fixed number of bands (usually ranging from 5 to 31) corresponding to specific frequency ranges. Users can visually manipulate sliders that represent these bands, effectively shaping the audio signal to meet their preferences. The straightforward design makes them popular for consumer audio systems.
Parametric Equalizers: More sophisticated than graphic equalizers, parametric equalizers allow users to adjust not only the amplitude of specific frequencies but also the frequency center and bandwidth (or Q factor). This flexibility makes parametric equalizers especially useful in professional audio settings for tailored sound shaping.

The Role of Digital Signal Processing (DSP)

Precision: DSP can fine-tune audio signals with remarkable accuracy, surpassing the capabilities of analog equalizers.
Customization: Users can create highly personalized sound profiles for different genres or listening environments, adjusting parameters dynamically for optimal experience.
Integration: DSP effortlessly integrates with various audio formats and electronic devices, making it suitable for the connected home environment.

Practical Considerations in Home Audio Design

While selecting equalizers for home audio systems, one must consider several factors:

Room Acoustics: The physical characteristics of a room, including its size and material, influence sound propagation. Understanding these aspects helps design a system that effectively compensates for such variances.
Listener Preferences: Ultimately, the effectiveness of an equalizer is subjective, relying heavily on individual sound preferences. A flat frequency response may appeal to some listeners, while others may prefer a more colored sound profile.
Signal Chain Integrity: Protecting the audio signal from degradation throughout the chain—from source to speaker—is crucial. An equalizer introduced into the signal path should not compromise audio quality, making high-fidelity components essential.

6. Common Issues in Equalizer Performance

6.1 Common Issues in Equalizer Performance

Audio equalizers serve the purpose of adjusting the balance between frequency components in an audio signal. While they enhance sound quality and provide customizability, performance challenges can impede their effectiveness. Understanding these common issues is essential for engineers and sound designers aiming for optimal audio fidelity.

Non-Linearity and Distortion

One primary concern in equalizer circuits is non-linearity, which can introduce unwanted distortion to the audio signal. Non-linear behavior is often characterized by a change in amplitude of the output signal that does not proportionately correspond to the input signal. This can arise from:

Component limitations: Active components like op-amps have finite gain bandwidth and may exhibit non-linear behavior when pushed beyond their specifications.
Passive components: Resistors and capacitors may also introduce non-linearities at extreme frequencies due to parasitic capacitances and inductances.

For instance, in a graphic equalizer, where multiple filters operate simultaneously, the accumulated non-linearity can lead to significant waveform distortion. This can be analyzed using harmonic distortion metrics, typically quantifying distortion by the ratio of output signal to its harmonic components.

Phase Shift

An essential characteristic of equalizers is their frequency response, often represented in terms of phase shift. Phase shift occurs when different frequency components are delayed by different amounts in the signal processing chain. If not compensated, this can lead to:

Comb filtering: This results from the interaction of multiple frequencies, leading to constructive and destructive interference that alters the perceived sound quality.
Temporal smearing: Delays in the signal can degrade clarity and articulation in audio playback.

To quantify phase shift, one can use the phase response function of the equalizer's transfer function H(f). This can be represented mathematically as:

$$ \phi(f) = \arctan\left(\frac{\text{Im}(H(f))}{\text{Re}(H(f))}\right) $$

Minimizing phase shift often involves careful design choices, such as selecting linear-phase filters, that preserve time domain integrity while equalizing.

Noise and Signal-to-Noise Ratio (SNR)

Another major issue affecting equalizer performance is noise. An equalizer must not only enhance desired frequencies but also maintain a high signal-to-noise ratio (SNR). Factors that contribute to excessive noise include:

Low-quality components: Using inexpensive op-amps or resistors can introduce thermal noise, compromising signal fidelity.
Power supply noise: Fluctuations or ripple in the supply voltage can translate into variations in the output signal.

To measure SNR, the equation below is utilized:

$$ \text{SNR} = 10 \log_{10}\left(\frac{P_{\text{signal}}}{P_{\text{noise}}}\right) $$

Maintaining a high SNR is crucial for applications like studio mixing and live sound reinforcement, where clarity of sound is paramount.

Limitations of Feedback Systems

Many equalizers use feedback systems to adjust gain at specific frequencies, leading to potential instability issues. Feedback can amplify noise, introducing oscillations or undesirable resonances. In addition, when feedback loops are incorrectly configured, they can lead to:

Over-modulation: Excessive feedback can result in signal clipping, distorting the audio.
Instability in frequency response: Sudden changes in signal can make the response unpredictable, particularly in dynamic audio situations.

Stability criteria for these systems can often be analyzed using the Lyapunov criterion, ensuring that feedback maintains performance without overshooting amplitude limits.

Through a detailed understanding of these common issues, engineers can design equalizer circuits that effectively enhance audio without compromising overall fidelity. This knowledge allows for more refined audio processing solutions that can cater to various practical applications, such as live performances, studio recordings, and broadcast media.

Diagram Description: The diagram would illustrate the concept of phase shift in equalizers, showing how different frequency components are delayed in the signal processing chain. This could clarify the effects of phase shift on audio performance and potential issues such as comb filtering.

6.1 Common Issues in Equalizer Performance

Non-Linearity and Distortion

Component limitations: Active components like op-amps have finite gain bandwidth and may exhibit non-linear behavior when pushed beyond their specifications.
Passive components: Resistors and capacitors may also introduce non-linearities at extreme frequencies due to parasitic capacitances and inductances.

Phase Shift

Comb filtering: This results from the interaction of multiple frequencies, leading to constructive and destructive interference that alters the perceived sound quality.
Temporal smearing: Delays in the signal can degrade clarity and articulation in audio playback.

To quantify phase shift, one can use the phase response function of the equalizer's transfer function H(f). This can be represented mathematically as:

$$ \phi(f) = \arctan\left(\frac{\text{Im}(H(f))}{\text{Re}(H(f))}\right) $$

Minimizing phase shift often involves careful design choices, such as selecting linear-phase filters, that preserve time domain integrity while equalizing.

Noise and Signal-to-Noise Ratio (SNR)

Low-quality components: Using inexpensive op-amps or resistors can introduce thermal noise, compromising signal fidelity.
Power supply noise: Fluctuations or ripple in the supply voltage can translate into variations in the output signal.

To measure SNR, the equation below is utilized:

$$ \text{SNR} = 10 \log_{10}\left(\frac{P_{\text{signal}}}{P_{\text{noise}}}\right) $$

Maintaining a high SNR is crucial for applications like studio mixing and live sound reinforcement, where clarity of sound is paramount.

Limitations of Feedback Systems

Over-modulation: Excessive feedback can result in signal clipping, distorting the audio.
Instability in frequency response: Sudden changes in signal can make the response unpredictable, particularly in dynamic audio situations.

Stability criteria for these systems can often be analyzed using the Lyapunov criterion, ensuring that feedback maintains performance without overshooting amplitude limits.

6.2 Measurement and Analysis Techniques

In the realm of audio equalization, effective measurement and analysis techniques are critical for both the design and evaluation of equalizer circuits. This section explores various methods employed to ensure that an equalizer achieves its intended functionality, including various signal analysis techniques.

Understanding Frequency Response

The frequency response of an audio equalizer is foundational for assessing its performance. It characterizes how the equalizer modifies the amplitude of different frequency components of an audio signal. Commonly, frequency response plots are generated, displaying the gain (in decibels) versus frequency (in hertz). Analyzing these plots allows engineers to determine the effectiveness of different equalization settings.

To acquire frequency response measurements, one can utilize a logarithmically spaced frequency sweep signal—a common practice in audio analysis. This signal is passed through the equalizer, and the resulting output is compared to the input by employing a measurement microphone and a spectrum analyzer, revealing the alterations made by the equalizer. The mathematical representation of the system can be expressed as:

$$ H(f) = \frac{V_{out}(f)}{V_{in}(f)} $$

Where H(f) is the frequency response function, V_{out}(f) is the output voltage at frequency f, and V_{in}(f) is the input voltage at the same frequency. This equation leads to important insights on band-specific adjustments made by the equalizer.

Time Domain Analysis

In addition to frequency response, time domain analysis is vital for understanding the transient characteristics of the equalizer. Analyzing time response helps assess the phase shift introduced by the equalization process. Phase distortion may lead to comb-filtering effects, which can compromise audio integrity, particularly in music production. Engineers often utilize impulse response testing to delve into this aspect.

An impulse response can be represented mathematically as follows:

$$ h(t) = \mathcal{F}^{-1} \{ H(f) \} $$

Where h(t) is the impulse response in the time domain, and \mathcal{F}^{-1} denotes the inverse Fourier transform. This transformation allows the analysis of how energy flows through the equalizer over time, enabling the identification of any unwanted artifacts.

Real-Time Measurement Techniques

For practical applications, real-time measurement techniques employ software tools and digital signal processors (DSP) that analyze incoming audio signals. Such tools can visualize frequency response and provide feedback on changes as they are applied, enabling an iterative tuning process. Technologies such as Fast Fourier Transform (FFT) algorithms are widely used for this purpose, allowing real-time analysis of audio inputs in a highly efficient manner. The basic principle allows us to transform a time-domain signal into its frequency-domain representation:

$$ X(f) = \sum_{n=0}^{N-1} x(n) e^{-j 2 \pi f n / N} $$

Here, X(f) is the output in the frequency domain, x(n) is the input time-domain signal, and N is the total number of samples. By leveraging FFT in audio equalization, engineers can measure and visualize in real-time the alterations applied across different frequencies.

Case Studies and Practical Applications

The importance of measurement and analysis in audio equalization can be highlighted through various case studies. For example, in live sound reinforcement, precise equalization adjustments based on frequency response measurements can significantly enhance sound quality and intelligibility, especially in adverse acoustic environments like concert halls or open-air venues.

Moreover, in studio environments, understanding time-domain characteristics can help prevent undesirable phase issues during mixing, ensuring that tracks blend seamlessly and maintaining the artistic intention of the producer. Thus, a robust method for measurement and analysis forms the backbone of successful audio engineering.

In summary, a well-rounded approach to measurement and analysis—encompassing frequency response, time-domain analysis, and real-time processing techniques—is essential for optimizing audio equalizer circuits and achieving high fidelity in sound reproduction.

Diagram Description: The diagram would illustrate the relationship between frequency response and gain in the frequency domain, as well as showing the impulse response in the time domain. It would clarify how the frequency response function affects the audio signal, which is complex to explain only in text.

6.2 Measurement and Analysis Techniques

Understanding Frequency Response

$$ H(f) = \frac{V_{out}(f)}{V_{in}(f)} $$

Time Domain Analysis

An impulse response can be represented mathematically as follows:

$$ h(t) = \mathcal{F}^{-1} \{ H(f) \} $$

Real-Time Measurement Techniques

$$ X(f) = \sum_{n=0}^{N-1} x(n) e^{-j 2 \pi f n / N} $$

Case Studies and Practical Applications

6.3 Tools for Circuit Testing

Testing audio equalizer circuits requires specialized tools that allow for accurate analysis and troubleshooting. Understanding these tools is vital, as they play a critical role in ensuring audio fidelity and performance. Below, we explore several tools and techniques essential for circuit testing, highlighting their functionalities and applications within the realm of audio engineering.

Oscilloscope

An oscilloscope is one of the most important diagnostic tools used in circuit testing. It provides a visual representation of electrical signals over time, allowing engineers to examine waveform characteristics such as amplitude, frequency, and distortion. Key features of an oscilloscope include:

Waveform visualization: Offers real-time monitoring of audio signals and their responses across the frequency spectrum.
Measurement capabilities: Can measure voltage levels, frequency, rise and fall times, and phase difference between signals.
Triggering options: Enables the user to stabilize repetitive signals, which is crucial for detailed analysis.

For audio equalizer circuits, oscilloscopes help identify clipping or distortion caused by overdriving an amplifier or incorrect equalization settings.

Multimeter

A digital multimeter (DMM) is another essential tool for circuit testing, providing basic electrical measurements, including voltage, current, and resistance. Applications of a multimeter in audio equalizer circuit testing include:

Verifying component values: Ensures that resistors, capacitors, and inductors are functioning as intended.
Testing connections: Helps troubleshoot continuity and identify potential short circuits or open circuits within the equalizer path.
Measuring power supply voltages: Critical for checking the operational stability of the circuit.

Audio Analyzer

An audio analyzer offers sophisticated test capabilities tailored specifically for audio applications. These devices can perform frequency response tests, total harmonic distortion (THD) analysis, and other essential metrics. Benefits of using an audio analyzer include:

Dynamic range measurements: Measures the range of signals an equalizer can handle, providing insight into its performance limits.
Real-time analysis: Quick feedback about responsiveness to input signals, useful for tuning equalizers during live sound applications.
Comparative analysis: Allows for juxtaposition of preset responses versus actual outputs, helping in refining audio quality.

Signal Generator

A signal generator is instrumental in testing audio circuits by providing a variety of input signals, such as sine waves, square waves, and white noise. How signal generators enhance circuit testing includes:

Input conditioning: Offers controlled inputs to evaluate how the equalizer modifies different signal types.
Frequency sweeps: Essential for examining the equalizer's frequency response and identifying any discontinuities or unwanted artifacts.
Noise generation: Can simulate real-world scenarios by injecting noise into the circuit for performance assessments.

Sound Level Meter

Finally, a sound level meter may seem ancillary, yet it plays a crucial role in the acoustic analysis of equalizer circuits. Key uses of sound level meters include:

Measuring sound pressure levels: Ensures that output levels conform to target specifications.
Impact assessment: Provides data on how adjustments in the equalizer impact perceived loudness and clarity in a room.
Calibration: Assists in calibrating audio systems for consistent performance across various environments.

In conclusion, utilizing these tools effectively allows for a comprehensive understanding of audio equalizer circuit performance. Whether tuning for optimal audio quality or troubleshooting issues, these instruments are essential for advanced circuit testing in audio engineering. The integration of accurate measurement and analysis tools is paramount in achieving professional-grade audio outcomes.

Diagram Description: The diagram would show the waveform representation of input and output signals from the audio equalizer circuit, along with measurements of key parameters like amplitude and frequency. This visual representation would clarify the signal transformations occurring at each testing stage.

6.3 Tools for Circuit Testing

Oscilloscope

Waveform visualization: Offers real-time monitoring of audio signals and their responses across the frequency spectrum.
Measurement capabilities: Can measure voltage levels, frequency, rise and fall times, and phase difference between signals.
Triggering options: Enables the user to stabilize repetitive signals, which is crucial for detailed analysis.

For audio equalizer circuits, oscilloscopes help identify clipping or distortion caused by overdriving an amplifier or incorrect equalization settings.

Multimeter

Verifying component values: Ensures that resistors, capacitors, and inductors are functioning as intended.
Testing connections: Helps troubleshoot continuity and identify potential short circuits or open circuits within the equalizer path.
Measuring power supply voltages: Critical for checking the operational stability of the circuit.

Audio Analyzer

Dynamic range measurements: Measures the range of signals an equalizer can handle, providing insight into its performance limits.
Real-time analysis: Quick feedback about responsiveness to input signals, useful for tuning equalizers during live sound applications.
Comparative analysis: Allows for juxtaposition of preset responses versus actual outputs, helping in refining audio quality.

Signal Generator

Input conditioning: Offers controlled inputs to evaluate how the equalizer modifies different signal types.
Frequency sweeps: Essential for examining the equalizer's frequency response and identifying any discontinuities or unwanted artifacts.
Noise generation: Can simulate real-world scenarios by injecting noise into the circuit for performance assessments.

Sound Level Meter

Finally, a sound level meter may seem ancillary, yet it plays a crucial role in the acoustic analysis of equalizer circuits. Key uses of sound level meters include:

Measuring sound pressure levels: Ensures that output levels conform to target specifications.
Impact assessment: Provides data on how adjustments in the equalizer impact perceived loudness and clarity in a room.
Calibration: Assists in calibrating audio systems for consistent performance across various environments.

7. Digital Equalizers: An Overview

7.1 Digital Equalizers: An Overview

Digital equalizers represent a significant advancement in audio processing, characterized by their precision and flexibility compared to traditional analog systems. Utilizing digital signal processing (DSP) techniques, these equalizers allow for the manipulation of audio signals with high fidelity and low noise. This subsection delves into the core functionalities, designs, and applications of digital equalizer circuits.

Understanding Digital Equalizers

At the heart of every digital equalizer lies a complex algorithm that processes the audio signal based on user-defined parameters. The fundamental operation involves adjusting the amplitude of various frequency bands to achieve the desired tonal balance in an audio mix. This process is typically executed through a combination of Fast Fourier Transform (FFT) techniques and finite impulse response (FIR) filters, which enables precise control over frequency response curves.

Key Components and Functionality

Digital equalizers primarily consist of the following components:

Analog-to-Digital Converter (ADC): Converts the analog audio signal into a digital format for processing.
DSP Processor: Executes the equalization algorithms, applying changes to the audio signal in real-time.
Digital-to-Analog Converter (DAC): Converts the processed digital signal back to an analog format for output.

This architecture offers superior ease of use and adaptability. Users can adjust specific frequency bands with notable precision, often through graphical user interfaces (GUIs) that visualize adjustments in real-time.

Technical Overview of Implementation

To implement a basic digital equalizer, one must understand and apply various mathematical techniques associated with signal processing. For instance, consider a simple equalizing filter implemented via an FIR filter. The filter’s output signal $ y[n] $ for any discrete input signal $ x[n] $ can be expressed as:

$$ y[n] = \sum_{m=0}^{M-1} h[m] \cdot x[n-m] $$

Here, $ h[m] $ denotes the filter coefficients, which can be designed to emphasize or attenuate specific frequency ranges. By optimizing these coefficients through methods such as windowing techniques or frequency sampling, one can tailor the equalization effects.

Real-World Applications

Digital equalizers are ubiquitous in various audio processing applications, including:

Music Production: Used in mixing and mastering to shape the overall sound of recordings.
Broadcasting: Enhances audio clarity and consistency during transmissions.
Live Sound Reinforcement: Adjusts the tonal character of live performances, ensuring sound fidelity in different environments.

With advancements in technology, the future of digital equalizers seems poised for further enhancements, integrating artificial intelligence for automatic tuning and optimization based on environmental acoustics.

Diagram Description: The diagram would visually represent the flow of an audio signal through the components of a digital equalizer, including the ADC, DSP processor, and DAC, showing how each part interacts with the audio signal before and after processing.

7.1 Digital Equalizers: An Overview

Understanding Digital Equalizers

Key Components and Functionality

Digital equalizers primarily consist of the following components:

Analog-to-Digital Converter (ADC): Converts the analog audio signal into a digital format for processing.
DSP Processor: Executes the equalization algorithms, applying changes to the audio signal in real-time.
Digital-to-Analog Converter (DAC): Converts the processed digital signal back to an analog format for output.

Technical Overview of Implementation

$$ y[n] = \sum_{m=0}^{M-1} h[m] \cdot x[n-m] $$

Real-World Applications

Digital equalizers are ubiquitous in various audio processing applications, including:

Music Production: Used in mixing and mastering to shape the overall sound of recordings.
Broadcasting: Enhances audio clarity and consistency during transmissions.
Live Sound Reinforcement: Adjusts the tonal character of live performances, ensuring sound fidelity in different environments.

7.2 Software Equalization Tools

The evolution of audio equalization has transcended hardware advancements, embracing sophisticated software solutions that have reshaped the landscape of sound engineering. Software equalization tools offer versatility, precision, and flexibility, making them indispensable in both professional studios and personal audio setups.

Unlike traditional analog equalizers that modify signals through physical components, software equalization tools rely on digital signal processing (DSP) techniques. This transition not only enhances the signal-to-noise ratio but also allows for more complex manipulations of audio frequencies. Engineers and audio enthusiasts alike can leverage a variety of algorithms tailored for specific applications, from music production to live sound reinforcement.

Digital Signal Processing Fundamentals

At the heart of software equalization tools is digital signal processing (DSP), which transforms audio signals into a numerical format that computers can manipulate. The key concept involves sampling the audio signal, converting it into discrete values, and applying mathematical operations to alter its frequency components. The process typically begins with the sampling theorem, which states that a signal can be perfectly reconstructed from its samples if it's sampled at twice its highest frequency. This gives rise to the Nyquist frequency, a critical principle that shapes the design of any digital audio system.

After sampling, these signals are manipulated using various algorithms. Most commonly, the Fast Fourier Transform (FFT) is employed to analyze the frequencies present in the audio signal. The FFT converts time-domain signals into frequency-domain representations, making it easier to identify which frequency bands require adjustment.

$$ X(f) = \sum_{n=0}^{N-1} x(n)e^{-j2\pi fn/N} $$

Here, $ X(f) $ denotes the frequency domain representation, while $ x(n) $ is the time-domain signal. By applying filters—a fundamental aspect of equalization—that either enhance or attenuate certain frequency ranges, the audio engineer can achieve the desired tonal balance.

Types of Software Equalizers

Software equalizers come in various forms, each catering to different needs and sound design philosophies. Common types include:

Parametric Equalizers: These allow for precise control over frequency, gain, and bandwidth (Q-factor). Engineers can sculpt the audio signal with high specificity, making them suitable for both corrective and creative applications.
Graphic Equalizers: Offering a series of fixed frequency bands, graphic equalizers provide visual feedback through sliders, allowing users to influence the overall tonal balance. They are widely used in live sound settings.
Shelf Equalizers: These adjust the frequencies above or below a specific threshold, making them effective for boosting bass or treble without affecting mid-range frequencies.

Each type has its place in the audio production process, from mixing and mastering to live performances. For instance, parametric equalizers are frequently used during mixing sessions to eliminate problematic resonances, while graphic equalizers may be applied in live sound reinforcement to shape the room acoustics dynamically.

Real-World Applications

The practical applications of software equalizers are both extensive and impactful. Music producers can create a polished final mix using these tools, balancing vocals and instruments to ensure clarity and presence within a track. In live settings, sound engineers employ graphic equalizers to adapt to varying acoustics, preventing feedback while enhancing vocal intelligibility.

Moreover, software equalizers find utility in post-production environments, where the restoration and enhancement of recorded audio is critical. By fine-tuning specific frequency ranges, engineers can bring out subtle details lost in original recordings, thus ensuring a high-quality listening experience.

As software continues to evolve, so too do the algorithms and capabilities of equalization tools. Advancements in artificial intelligence and machine learning are beginning to influence how equalizers operate, leading to automatic adjustments based on analyzed audio characteristics and user preferences.

Understanding software equalization tools not only empowers engineers to craft superior soundscapes but also allows researchers to explore the fascinating interplay between technology and auditory perception. As such, the future of audio engineering will undoubtedly continue to bridge the gap between practical toolsets and the evolving landscape of sound creativity.

Diagram Description: A diagram could illustrate the concept of digital signal processing, specifically showing the flow from an audio signal input, through the sampling process, and finally to various filtering stages including FFT analysis. This would visually represent the transformations that occur in software equalization tools.

7.2 Software Equalization Tools

Digital Signal Processing Fundamentals

$$ X(f) = \sum_{n=0}^{N-1} x(n)e^{-j2\pi fn/N} $$

Types of Software Equalizers

Software equalizers come in various forms, each catering to different needs and sound design philosophies. Common types include:

Parametric Equalizers: These allow for precise control over frequency, gain, and bandwidth (Q-factor). Engineers can sculpt the audio signal with high specificity, making them suitable for both corrective and creative applications.
Graphic Equalizers: Offering a series of fixed frequency bands, graphic equalizers provide visual feedback through sliders, allowing users to influence the overall tonal balance. They are widely used in live sound settings.
Shelf Equalizers: These adjust the frequencies above or below a specific threshold, making them effective for boosting bass or treble without affecting mid-range frequencies.

Real-World Applications

7.3 Trends in Audio Processing

The evolution of audio processing over recent decades has been marked by significant advancements driven by rapid technological developments and changing consumer expectations. One major trend is the transition from analog to digital audio processing, which has not only enhanced sound quality but also expanded the possibilities for sound manipulation. This shift has paved the way for more sophisticated audio equalizer circuits, leveraging digital signal processing (DSP) techniques that were previously confined to theoretical applications. Digital audio equalizers utilize algorithms to modify audio signals with a precision unattainable by analog circuits. This opens new avenues for audio engineers, who can now implement complex filtering techniques such as adaptive filtering and dynamic range compression. Adaptive equalizers can adjust their parameters in real time, responding to varying audio conditions, which has become essential in live sound reinforcement and studio environments. As audio processing continues to evolve, the integration of machine learning algorithms is becoming increasingly prevalent. These systems can learn and adapt to user preferences, delivering a personalized audio experience. Such advancements lead to intelligent equalization, where the circuit learns from the environment and adapts accordingly—an area ripe for development in consumer electronics, automotive audio systems, and professional audio setups. Furthermore, the emergence of immersive audio formats, such as Dolby Atmos and DTS:X, emphasizes spatial audio processing. Equalization techniques must now account for multiple dimensions of sound, necessitating new circuit designs that can process audio signals in three-dimensional space. The challenge lies in maintaining fidelity while ensuring that audio remains immersive, which often calls for sophisticated algorithms capable of simulating sound waves' behavior in a physical environment. The convergence of audio processing with other technologies is also noteworthy. For instance, voices recognized using natural language processing need to be enhanced for clarity in smart devices, influencing the design of targeted equalizers that can specifically tackle intelligibility issues. Additionally, the proliferation of audio streaming services has spurred demand for high-quality audio delivery, leading to the adoption of High-Resolution Audio (HRA) formats, which necessitate advanced equalization methods to fully realize the potential of higher sample rates and bit depths. Moreover, the integration of network capabilities in modern audio systems allows for real-time updates to equalizer settings based on user feedback or sound analysis data. This trend fosters collaboration between users and curators, creating a more interactive sound experience. As we look toward the future, it is clear that audio processing will continue to be heavily influenced by emerging technologies, placing audio equalizer circuits at the forefront of this evolution. In conclusion, the current trends in audio processing signal a shift towards more intelligent, adaptive, and immersive audio experiences, significantly impacting both the consumer market and professional applications. As innovation persists, designers and engineers must remain agile, integrating new techniques and responding to the evolving landscape of audio technology.

7.3 Trends in Audio Processing

8. Books on Audio Engineering

8.1 Books on Audio Engineering

Audio Engineering Explained by Douglas Self — This book covers foundational principles, advanced topics, and practical applications in audio engineering. Douglas Self offers in-depth analyses of various components and systems that form the backbone of modern audio equipment.
Psychoacoustics: Facts and Models by Eberhard Zwicker and Hugo Fastl — Offering a comprehensive overview of the human perception of sound, this book is essential for understanding the psychoacoustic principles that underlie audio equalizer designs. It provides scientific explanations and models used by audio engineers.
The Audio Dictionary by Glenn White and Gary J. Louie — An invaluable reference, this dictionary covers a vast array of audio engineering terms and concepts, providing clear definitions and context. It is an indispensable tool for both novices and seasoned professionals.
Modern Recording Techniques by David Miles Huber — This book serves as a comprehensive guide to audio recording, mixing, and mastering. It highlights the technological advancements and methodologies that are relevant to constructing and understanding sophisticated audio equalizer circuits.
The Art of Mixing by David Gibson — Specifically addressing audio mixing, this book uses visual techniques to communicate complex concepts. It skillfully illustrates how different audio components — such as equalizers — contribute to a balanced and pleasing sound environment.
Sound and Recording: An Introduction by Francis Rumsey and Tim McCormick — Aimed at providing a solid base in sound recording techniques, this book includes detailed discussions on the roles and functions of audio equalizers within broader recording systems. It is ideal for both beginners and more advanced learners.
Sound System Engineering by Don Davis and Eugene Patronis Jr. — Focused on the principles and practices within sound system design, this work is valuable for engineers interested in learning about the integration and optimization of audio components, including equalizers, in professional audio systems.

8.1 Books on Audio Engineering

Audio Engineering Explained by Douglas Self — This book covers foundational principles, advanced topics, and practical applications in audio engineering. Douglas Self offers in-depth analyses of various components and systems that form the backbone of modern audio equipment.
Psychoacoustics: Facts and Models by Eberhard Zwicker and Hugo Fastl — Offering a comprehensive overview of the human perception of sound, this book is essential for understanding the psychoacoustic principles that underlie audio equalizer designs. It provides scientific explanations and models used by audio engineers.
The Audio Dictionary by Glenn White and Gary J. Louie — An invaluable reference, this dictionary covers a vast array of audio engineering terms and concepts, providing clear definitions and context. It is an indispensable tool for both novices and seasoned professionals.
Modern Recording Techniques by David Miles Huber — This book serves as a comprehensive guide to audio recording, mixing, and mastering. It highlights the technological advancements and methodologies that are relevant to constructing and understanding sophisticated audio equalizer circuits.
The Art of Mixing by David Gibson — Specifically addressing audio mixing, this book uses visual techniques to communicate complex concepts. It skillfully illustrates how different audio components — such as equalizers — contribute to a balanced and pleasing sound environment.
Sound and Recording: An Introduction by Francis Rumsey and Tim McCormick — Aimed at providing a solid base in sound recording techniques, this book includes detailed discussions on the roles and functions of audio equalizers within broader recording systems. It is ideal for both beginners and more advanced learners.
Sound System Engineering by Don Davis and Eugene Patronis Jr. — Focused on the principles and practices within sound system design, this work is valuable for engineers interested in learning about the integration and optimization of audio components, including equalizers, in professional audio systems.

8.2 Academic Journals and Papers

Parametric Equalizers for Audio Applications — This paper provides a comprehensive study on the design and utilization of parametric equalizers in audio applications, discussing both theoretical and practical implementations.
Optimization Techniques for Digital Audio Equalizers — Explore various optimization techniques in digital equalizer design. This paper is valuable for those interested in enhancing the efficiency and performance of digital audio processing systems.
The Effect of Equalization on Audio Quality — This research investigates how different equalization methods impact audio quality, providing insights into both subjective and objective assessments.
Real-Time Audio Equalization Algorithms — Delve into real-time audio equalization, focusing on algorithm development for adaptive and responsive equalizer designs, crucial for live performance settings.
Comparative Study of Analog and Digital Audio Equalizers — This study compares the effectiveness and efficiency of analog versus digital equalizers, providing valuable insights for engineers making design decisions.
Advanced Filters for Audio Signal Processing — Examine advanced filtering techniques used in audio signal processing, offering a deep dive into methods that can be applied in equalizer circuit designs.
Analogue Audio Equalization Using Active Filter Components — Discover the principles behind analog equalizers utilizing active components, emphasizing practical circuit implementation and theoretical challenges.

8.2 Academic Journals and Papers

Parametric Equalizers for Audio Applications — This paper provides a comprehensive study on the design and utilization of parametric equalizers in audio applications, discussing both theoretical and practical implementations.
Optimization Techniques for Digital Audio Equalizers — Explore various optimization techniques in digital equalizer design. This paper is valuable for those interested in enhancing the efficiency and performance of digital audio processing systems.
The Effect of Equalization on Audio Quality — This research investigates how different equalization methods impact audio quality, providing insights into both subjective and objective assessments.
Real-Time Audio Equalization Algorithms — Delve into real-time audio equalization, focusing on algorithm development for adaptive and responsive equalizer designs, crucial for live performance settings.
Comparative Study of Analog and Digital Audio Equalizers — This study compares the effectiveness and efficiency of analog versus digital equalizers, providing valuable insights for engineers making design decisions.
Advanced Filters for Audio Signal Processing — Examine advanced filtering techniques used in audio signal processing, offering a deep dive into methods that can be applied in equalizer circuit designs.
Analogue Audio Equalization Using Active Filter Components — Discover the principles behind analog equalizers utilizing active components, emphasizing practical circuit implementation and theoretical challenges.

8.3 Online Resources and Tutorials

Designing An Audio Equalizer Circuit Using Op-Amps — This article provides a comprehensive guide to designing audio equalizer circuits with operational amplifiers, including practical components selection, and schematic examples.
Electronics Tutorials - Audio Equalizer Design — Offers a detailed exploration of the theory and design principles behind audio equalizers, ranging from simple passive designs to more complex active circuits.
Designing a 5-Band Graphic Equalizer — Explains the working and design considerations for building a 5-band graphic equalizer, complete with schematics and component descriptions.
YouTube: Audio Equalizer Circuit Tutorial — A video tutorial that demonstrates the step-by-step assembly and testing of an audio equalizer circuit, with visual aids for better understanding.
Elliott Sound Products — Contains extensive resources and articles about audio circuits, including various types of equalizer designs and other audio processing tools.
Audio Equalizer Circuit Diagram and Working — Discusses the circuit diagram of a simple audio equalizer and explains its working principles in detail, suitable for both hobbyists and professionals.

8.3 Online Resources and Tutorials

Designing An Audio Equalizer Circuit Using Op-Amps — This article provides a comprehensive guide to designing audio equalizer circuits with operational amplifiers, including practical components selection, and schematic examples.
Electronics Tutorials - Audio Equalizer Design — Offers a detailed exploration of the theory and design principles behind audio equalizers, ranging from simple passive designs to more complex active circuits.
Designing a 5-Band Graphic Equalizer — Explains the working and design considerations for building a 5-band graphic equalizer, complete with schematics and component descriptions.
YouTube: Audio Equalizer Circuit Tutorial — A video tutorial that demonstrates the step-by-step assembly and testing of an audio equalizer circuit, with visual aids for better understanding.
Elliott Sound Products — Contains extensive resources and articles about audio circuits, including various types of equalizer designs and other audio processing tools.
Audio Equalizer Circuit Diagram and Working — Discusses the circuit diagram of a simple audio equalizer and explains its working principles in detail, suitable for both hobbyists and professionals.