Flyback Converter Design
1. Basic Operating Principle
1.1 Basic Operating Principle
The flyback converter operates as a switched-mode power supply (SMPS) that efficiently steps up or down DC voltage while providing galvanic isolation. Unlike conventional buck or boost converters, it stores energy in the transformer's magnetizing inductance during the switch-on phase and releases it to the output during the switch-off phase. This dual-phase operation makes it particularly useful in applications requiring high voltage conversion ratios and isolation, such as offline power supplies and LED drivers.
Energy Storage and Transfer Mechanism
When the MOSFET switch (Q1) is turned on, the primary winding of the transformer is connected to the input voltage (Vin), causing current to ramp up linearly. The transformer's core stores energy in its magnetic field, but due to the dot convention, the secondary-side diode (D1) remains reverse-biased, preventing energy transfer to the output. The governing equation for the primary current (Ip) during this phase is:
where Lp is the primary-side magnetizing inductance. The energy stored (Estored) in the core is:
Energy Release Phase
When Q1 turns off, the collapsing magnetic field induces a voltage on the secondary winding, forward-biasing D1 and transferring energy to the output capacitor (Cout) and load. The secondary current (Is) decays linearly, and the output voltage is regulated by the turns ratio (N = Np/Ns) and duty cycle (D). The output voltage (Vout) in discontinuous conduction mode (DCM) is:
Key Practical Considerations
- Transformer Design: The transformer must handle high peak currents and avoid saturation, requiring careful selection of core material (e.g., ferrite) and air-gapping.
- Leakage Inductance: Parasitic leakage inductance causes voltage spikes during switch turn-off, necessitating snubber circuits or active clamping.
- Control Mode: DCM offers simpler control but higher peak currents, while continuous conduction mode (CCM) reduces RMS currents but complicates feedback stability.
The flyback converter's discontinuous energy transfer makes it inherently suitable for wide input voltage ranges, but it requires precise control of switching timing to maintain efficiency and avoid transformer saturation. Modern implementations often integrate pulse-width modulation (PWM) controllers with feedback loops to regulate output voltage under varying load conditions.
1.2 Key Components and Their Roles
Transformer
The flyback transformer operates as a coupled inductor rather than a traditional transformer, storing energy during the switch-on phase and releasing it during the switch-off phase. The primary inductance Lp determines the energy storage capacity:
where Ipk is the peak primary current. The turns ratio N = Np/Ns directly influences the output voltage:
High-permeability ferrite cores with an air gap are typically used to prevent saturation while maintaining sufficient energy storage.
Power Switch (MOSFET)
The MOSFET must withstand the maximum drain-source voltage VDS(max), which includes input voltage and reflected secondary voltage:
Fast switching (tr, tf < 50 ns) minimizes switching losses, while low RDS(on) reduces conduction losses. Gate drive circuitry must supply sufficient charge to achieve rapid transitions.
Output Rectifier
The diode's reverse recovery time trr critically impacts efficiency. Schottky diodes are preferred for low-voltage outputs (< 100 V) due to their near-zero recovery time. For higher voltages, ultrafast Si diodes or SiC Schottky diodes are used. The diode's peak inverse voltage rating must exceed:
Output Capacitor
The capacitor must handle high ripple current while maintaining stable output voltage. The required capacitance depends on the allowable output voltage ripple ΔVout:
Low-ESR aluminum electrolytic or polymer capacitors are typically used, with ceramic capacitors often added in parallel for high-frequency decoupling.
Control IC and Feedback Network
Modern PWM controllers (e.g., UC384x series) provide precise duty cycle control through voltage-mode or current-mode feedback. The compensation network must be designed for stable operation across all load conditions. Optocouplers provide isolation in the feedback path, with the TL431 shunt regulator commonly used as a voltage reference.
Snubber Circuit
The RCD snubber suppresses voltage spikes caused by transformer leakage inductance:
The snubber capacitor value is chosen to limit the voltage rise time, while the resistor dissipates the stored energy.
1.3 Comparison with Other Converter Topologies
The flyback converter is often compared to other isolated and non-isolated DC-DC converter topologies, such as the forward converter, push-pull converter, and buck-boost converter. Each topology has distinct advantages and trade-offs in terms of efficiency, component stress, cost, and application suitability.
Flyback vs. Forward Converter
The forward converter, like the flyback, uses a transformer for isolation, but operates differently. While the flyback stores energy in the transformer's magnetizing inductance during the switch-on phase and releases it during the off phase, the forward converter transfers energy directly to the output during the switch-on phase. Key differences include:
- Energy Storage: Flyback relies on transformer inductance, whereas forward converters require an output inductor.
- Peak Current Stress: Flyback converters exhibit higher peak currents due to discontinuous conduction, increasing MOSFET and diode stress.
- Output Ripple: Forward converters typically have lower output ripple due to the output filter inductor.
Mathematically, the output voltage of a flyback converter in discontinuous conduction mode (DCM) is given by:
where D is the duty cycle, RL is the load resistance, Lm is the magnetizing inductance, and fs is the switching frequency.
Flyback vs. Push-Pull Converter
Push-pull converters use two primary switches and a center-tapped transformer, offering higher power capability and better transformer utilization. Comparative aspects include:
- Transformer Core Utilization: Push-pull converters avoid core saturation by bidirectional excitation, whereas flyback converters require an air gap, leading to higher leakage inductance.
- Efficiency: Push-pull converters achieve higher efficiency (>90%) at higher power levels (>100W), while flyback efficiency degrades due to switching and conduction losses.
- Complexity: Push-pull designs demand precise switch timing to avoid shoot-through, increasing control complexity.
Flyback vs. Buck-Boost Converter
Non-isolated buck-boost converters share functional similarities with flyback converters, but lack galvanic isolation. Key contrasts:
- Isolation: Flyback provides voltage isolation, critical for safety in AC-DC applications (e.g., power supplies).
- Component Count: Buck-boost converters use fewer components (no transformer), reducing cost and board space.
- Voltage Range: Flyback converters support wide input/output voltage ranges, making them suitable for universal input supplies (90V–265V AC).
Practical Considerations
Flyback converters dominate low-to-medium power applications (<500W) due to their simplicity and cost-effectiveness. However, at higher power levels, forward or LLC resonant converters are preferred for their superior efficiency and thermal performance. In high-voltage scenarios (e.g., LED drivers), flyback's inherent voltage clamping simplifies snubber design compared to forward converters.
2. Transformer Design and Selection
2.1 Transformer Design and Selection
Core Material and Geometry
The choice of core material significantly impacts the efficiency and thermal performance of a flyback transformer. Ferrite cores (Mn-Zn or Ni-Zn) are preferred due to their high resistivity, low core losses at high frequencies, and saturation flux density (Bsat) typically between 0.2–0.5 T. Powdered iron cores are avoided due to excessive eddy current losses.
The core geometry (e.g., E-core, toroidal, or planar) affects winding capacitance and leakage inductance. An E-core with a gapped center leg is common, as the air gap stores energy and prevents saturation. The required gap length (lg) is derived from:
where μ0 is permeability of free space, μr is relative permeability, Np is primary turns, Ae is effective core area, and Lp is primary inductance.
Primary and Secondary Turns Calculation
The primary turns (Np) are determined by Faraday’s law, ensuring the core does not saturate at peak current:
where Vin is input voltage, Dmax is maximum duty cycle, fsw is switching frequency, and ΔB is flux swing (typically ≤ 0.3·Bsat).
The secondary turns (Ns) are calculated from the output voltage (Vout) and reflected voltage (VR):
where VD is diode forward voltage. The turns ratio (n = Np/Ns) must also account for leakage inductance effects.
Winding Configuration and Losses
Interleaved winding (primary-secondary-primary) reduces leakage inductance and proximity losses. The AC resistance (Rac) of windings is frequency-dependent due to skin and proximity effects:
where d is conductor diameter and δ is skin depth. Litz wire or thin foils mitigate this effect at high frequencies (>100 kHz).
Practical Considerations
- Insulation: Use reinforced isolation (e.g., triple-insulated wire) for safety-critical applications.
- Thermal management: Core losses (Pcore = k \cdot f_{sw}^\alpha \cdot \Delta B^\beta) and copper losses must be derated for temperature rise.
- Regulatory compliance: Creepage and clearance distances must meet IEC/EN 60950 for offline converters.
2.2 Switching Frequency and Duty Cycle
The switching frequency (fsw) and duty cycle (D) are critical parameters in flyback converter design, directly influencing efficiency, transformer size, and output voltage regulation. These parameters must be carefully optimized to balance switching losses, magnetic component size, and transient response.
Switching Frequency Trade-offs
Higher switching frequencies reduce the required inductance and transformer size, enabling compact designs. However, they also increase switching losses due to:
- Gate charge dissipation: MOSFET turn-on/turn-off losses scale linearly with fsw.
- Core losses: Hysteresis and eddy current losses follow Steinmetz's equation, approximately proportional to fswα (where α ≈ 1.3–2.5).
- Skin effect: AC resistance in windings increases with frequency.
Practical designs typically operate between 50 kHz and 1 MHz, with industrial designs favoring 65–250 kHz for optimal efficiency.
Duty Cycle Derivation
The duty cycle defines the ON-time fraction of the switching period. For a flyback converter in discontinuous conduction mode (DCM), the output voltage Vout relates to the input voltage Vin and turns ratio N as:
Rearranging for D yields:
In continuous conduction mode (CCM), the relationship becomes:
Practical Constraints
The duty cycle must adhere to:
- Minimum ON-time: Limited by controller/mosfet capabilities (typically 100–500 ns).
- Maximum duty cycle: Usually capped at 50–75% to ensure transformer reset.
- Transient response: Lower D provides faster load regulation but requires higher peak currents.
Design Example
For a flyback converter with Vin = 48 V, Vout = 12 V, and N = 0.25 operating in DCM:
At fsw = 100 kHz, the ON-time would be:
2.3 Output Voltage Regulation
Output voltage regulation in a flyback converter is critical for maintaining stable DC output despite variations in input voltage, load current, and component tolerances. The primary control mechanism involves a feedback loop that adjusts the duty cycle of the switching transistor to compensate for deviations from the desired output voltage.
Feedback Control Mechanism
The regulation loop typically employs a voltage divider to sample the output voltage, which is then compared to a reference voltage using an error amplifier (often a TL431 or an operational amplifier). The error signal modulates the duty cycle via a pulse-width modulation (PWM) controller such as UC3842 or LT1241.
Where:
- \( V_{out} \): Output voltage
- \( N_s / N_p \): Secondary-to-primary turns ratio
- \( D \): Duty cycle
- \( V_{in} \): Input voltage
Compensation Network Design
To ensure stability, a Type II or Type III compensation network is often used, introducing poles and zeros to shape the loop gain. The transfer function of the error amplifier with compensation can be derived as:
Key considerations for compensation:
- Crossover frequency: Typically set at 1/10th of the switching frequency.
- Phase margin: Should exceed 45° to avoid oscillations.
- Gain margin: Must be sufficient to prevent instability under load transients.
Practical Implementation Challenges
In real-world applications, parasitic elements such as leakage inductance and winding capacitance can introduce high-frequency noise, requiring additional filtering. A secondary-side LC filter is often employed to attenuate switching ripple:
Where:
- \( \Delta V_{ripple} \): Output voltage ripple
- \( I_{out} \): Load current
- \( f_{sw} \): Switching frequency
- \( C_{out} \): Output capacitance
Optocoupler Isolation in Feedback
Since flyback converters often require galvanic isolation, an optocoupler (e.g., PC817) is used to transmit the feedback signal from the secondary to the primary side. The optocoupler's current transfer ratio (CTR) must be accounted for in loop gain calculations:
Where:
- \( I_C \): Collector current
- \( I_F \): Forward current
Variations in CTR with temperature and aging necessitate careful selection and biasing of the optocoupler to maintain consistent loop performance.
Load and Line Regulation Metrics
Regulation performance is quantified by:
- Load regulation: \( \frac{\Delta V_{out}}{V_{out}} \) for a given \( \Delta I_{load} \)
- Line regulation: \( \frac{\Delta V_{out}}{V_{out}} \) for a given \( \Delta V_{in} \)
High-performance designs achieve < 1% regulation for both metrics, often requiring iterative tuning of the compensation network and careful PCB layout to minimize parasitic impedances.
This section provides a rigorous, mathematically grounded explanation of output voltage regulation in flyback converters, covering feedback mechanisms, compensation design, practical challenges, and performance metrics—all structured for advanced readers. The HTML is properly formatted with hierarchical headings, mathematical derivations, and clear technical explanations.2.4 Input and Output Filtering
Input and output filtering in a flyback converter is critical for mitigating conducted electromagnetic interference (EMI), reducing ripple voltage, and ensuring stable operation under varying load conditions. The flyback topology inherently generates high-frequency switching noise due to discontinuous current flow in both the primary and secondary sides, necessitating robust filtering strategies.
Input Filter Design
The input filter primarily suppresses high-frequency noise generated by the switching MOSFET and prevents it from propagating back into the power source. A typical input filter consists of a combination of inductors (Lin) and capacitors (Cin) arranged in an LC or π-filter configuration.
To minimize reflected ripple current, the input filter's cutoff frequency (fc) must be sufficiently lower than the switching frequency (fsw):
Common-mode chokes are often incorporated to attenuate differential-mode and common-mode noise. The required attenuation can be derived from regulatory standards such as CISPR 32 or FCC Part 15, which impose limits on conducted emissions.
Output Filter Design
The output filter smooths the discontinuous current from the secondary-side rectifier, reducing output voltage ripple. A low-ESR electrolytic or ceramic capacitor (Cout) is typically used, often in parallel with a smaller high-frequency bypass capacitor to improve transient response.
Where D is the duty cycle and ESR is the equivalent series resistance of the output capacitor. For high-current applications, an additional LC post-filter may be employed to further reduce ripple:
Here, ΔIL is the desired inductor current ripple, usually set to 20-40% of the rated output current.
Practical Considerations
- Component parasitics: Stray inductance and capacitance can lead to unintended resonances, requiring careful PCB layout and component selection.
- Thermal management: High ripple currents increase power dissipation in capacitors and inductors, necessitating derating or active cooling.
- Stability: The output filter introduces phase lag, which must be accounted for in the feedback loop compensation.
In high-power designs, active filtering techniques such as synchronous rectification or feedforward control may be employed to further improve efficiency and reduce component stress.
3. Component Selection and Sizing
3.1 Component Selection and Sizing
Transformer Design Considerations
The transformer in a flyback converter serves dual roles: energy storage and galvanic isolation. Its design begins with determining the primary inductance \( L_p \), which governs energy transfer per switching cycle. The required inductance is derived from the power balance equation:
where \( V_{in(min)} \) is the minimum input voltage, \( D_{max} \) is the maximum duty cycle (typically ≤0.5 for discontinuous conduction mode), \( P_{out} \) is the output power, \( f_{sw} \) is the switching frequency, and \( \eta \) is the estimated efficiency (usually 0.7–0.85).
The transformer turns ratio \( N \) is calculated based on the voltage conversion ratio and desired reflected output voltage:
Here, \( V_D \) is the diode forward voltage, and \( V_R \) is the reflected voltage (typically 80–150V for universal input designs). Core selection follows the area-product method, ensuring sufficient flux swing \( \Delta B \) (≤0.2T for ferrites) to avoid saturation:
where \( A_e \) is the core cross-sectional area, \( A_w \) is the window area, \( I_{pk} \) is the peak primary current, \( K_u \) is the winding fill factor (0.2–0.4), and \( J \) is the current density (3–5 A/mm²).
Power Switch Selection
The MOSFET must withstand the maximum drain-source voltage \( V_{DS(max)} \), which includes input voltage and reflected output voltage spikes:
where \( V_{spike} \) accounts for leakage inductance effects (20–30% of \( V_{DS(max)} \)). The RMS current rating \( I_{D(RMS)} \) is:
For high-frequency designs (≥100 kHz), GaN FETs or superjunction MOSFETs are preferred due to lower \( Q_g \) and \( C_{oss} \).
Output Diode and Capacitor Sizing
The output diode’s reverse voltage rating must exceed:
Fast-recovery diodes (e.g., SiC Schottky) minimize reverse recovery losses. The output capacitor \( C_{out} \) is sized to limit voltage ripple \( \Delta V_{out} \):
Low-ESR polymer or ceramic capacitors are ideal for high-frequency ripple suppression.
Snubber Network Design
An RCD snubber suppresses voltage spikes from leakage inductance \( L_{lk} \). The snubber capacitor \( C_{snub} \) is:
where \( V_{snub} \) is the desired clamping voltage (typically 1.5× the reflected voltage). The resistor \( R_{snub} \) dissipates stored energy:
Practical implementations often use TVS diodes for faster transient response.
Control Loop Components
The feedback network (e.g., TL431 with optocoupler) must compensate for the right-half-plane zero inherent to flyback converters. The crossover frequency \( f_c \) should satisfy:
Type II or III compensators are common, with component values derived from the modulator gain and plant transfer function.
3.2 PCB Layout and Thermal Management
Critical PCB Layout Considerations
The PCB layout of a flyback converter significantly impacts its performance, efficiency, and electromagnetic interference (EMI) characteristics. High-frequency switching (typically 50 kHz to 1 MHz) necessitates careful attention to parasitic inductance and capacitance, which can lead to voltage spikes, ringing, and increased losses.
Key design principles:
- Minimize high-current loop areas to reduce parasitic inductance and radiated EMI. The primary-side switch (MOSFET), transformer, and input capacitor should form the smallest possible loop.
- Separate high-voltage and low-voltage sections to prevent capacitive coupling and noise injection. Maintain adequate creepage and clearance distances per IEC 60950 or relevant standards.
- Use a solid ground plane for the secondary-side return path to minimize ground bounce and noise coupling.
- Route high dv/dt and di/dt traces (e.g., drain of MOSFET, transformer windings) away from sensitive analog sections such as feedback networks or control ICs.
Thermal Management Strategies
Power dissipation in a flyback converter occurs primarily in the MOSFET, rectifier diode, and transformer. Effective thermal design ensures reliability and prevents thermal runaway.
Heat dissipation mechanisms:
- Conduction: Use wide copper traces or pours for high-current paths to reduce resistive losses. The thermal resistance of a trace is given by:
where L is trace length, κ is copper thermal conductivity (385 W/m·K), and A is cross-sectional area.
- Convection: Increase surface area with thermal relief patterns or heatsinks. Forced airflow may be necessary in high-power designs.
- Radiation: Use dark-colored solder mask or exposed copper to enhance infrared emission, though this is typically secondary to conduction/convection.
Component Placement and Heat Spreading
Place high-power components (MOSFET, diode) near the board edge or with access to heatsinks. Thermal vias under these components transfer heat to inner or bottom layers. The thermal resistance of a via array is approximated by:
where N is the number of vias, t is PCB thickness, and r is via radius. A typical 0.3 mm via in a 1.6 mm FR4 board has ~80°C/W per via; arrays of 10-20 vias are common under power devices.
EMI Mitigation Techniques
Flyback converters generate high-frequency noise due to discontinuous currents. Proper layout reduces both conducted and radiated emissions:
- Snubber circuits (RC or RCD) should be placed adjacent to the MOSFET/diode they protect, with minimal trace length.
- Shielded transformers or copper tape over unshielded designs reduces magnetic field radiation.
- Differential-mode noise is minimized by tight input/output capacitor placement, while common-mode noise requires Y-capacitors (e.g., 1-2.2 nF) from primary/secondary to ground.
Practical Layout Example
A well-designed flyback PCB features:
- Primary high-current loop (input cap → transformer → MOSFET → ground) kept under 10 cm².
- Secondary rectifier and output cap loop similarly minimized.
- Control IC placed away from switching nodes, with feedback traces routed as short as possible.
- Thermal relief cuts in ground planes under high-frequency switching nodes to reduce capacitive coupling.
Thermal simulations (e.g., Ansys Icepak or COMSOL) validate design choices by modeling temperature distribution under worst-case loading. Empirical verification with infrared thermography ensures no localized hot spots exceed component ratings.
Protection Circuits and Safety Measures
Overvoltage Protection (OVP)
Flyback converters are susceptible to voltage spikes due to leakage inductance and parasitic elements. Overvoltage protection (OVP) circuits clamp excessive voltages to prevent damage to the MOSFET and output diodes. A common approach employs a transient voltage suppressor (TVS) or a zener diode in conjunction with a snubber circuit. The clamping voltage \( V_{clamp} \) is derived as:
where \( V_{out} \) is the nominal output voltage and \( V_{z} \) is the breakdown voltage of the zener diode. For robust protection, the TVS diode must be rated for the peak power dissipation:
Overcurrent Protection (OCP)
Primary-side current sensing using a shunt resistor or a current transformer ensures fast response to overcurrent conditions. The current limit \( I_{limit} \) is set by the controller’s reference voltage \( V_{ref} \) and sense resistor \( R_{sense} \):
For secondary-side OCP, a dedicated IC like the UC3843 integrates cycle-by-cycle current limiting. Hysteresis control prevents false triggering during transient loads.
Thermal Protection
Junction temperature monitoring prevents thermal runaway. A negative temperature coefficient (NTC) thermistor placed near the MOSFET or transformer feeds back to the controller. The shutdown threshold \( T_{j(max)} \) follows:
where \( R_{th(j-a)} \) is the thermal resistance junction-to-ambient and \( P_{diss} \) is the power dissipation.
Soft-Start and Inrush Limiting
To mitigate inrush currents during startup, a soft-start capacitor \( C_{ss} \) controls the PWM ramp-up time \( t_{ss} \):
where \( I_{charge} \) is the internal current source of the controller. A series NTC or MOSFET-based active limiter further reduces stress on bulk capacitors.
Isolation and Safety Compliance
For AC-DC flyback converters, reinforced isolation (e.g., IEC 62368-1) mandates:
- Creepage and clearance distances ≥ 6.4 mm for 300 VAC.
- Double insulation between primary and secondary windings.
- Y-capacitors (Class-X/Y) for EMI suppression while maintaining leakage current limits.
4. Efficiency Calculations and Losses
4.1 Efficiency Calculations and Losses
Power Loss Components in a Flyback Converter
The efficiency η of a flyback converter is determined by the ratio of output power Pout to input power Pin:
Losses in a flyback converter arise from several sources, categorized as conduction losses, switching losses, magnetic losses, and parasitic effects. The total power dissipation Ploss is the sum of these individual components:
Conduction Losses
Conduction losses occur due to resistive elements in the circuit, primarily the MOSFET on-resistance RDS(on) and the diode forward voltage drop VF.
The MOSFET conduction loss Pcond,MOSFET is given by:
where IRMS is the root-mean-square current through the MOSFET. For a flyback converter operating in discontinuous conduction mode (DCM), IRMS is derived from the peak current Ipk and duty cycle D:
The diode conduction loss Pcond,Diode is:
Switching Losses
Switching losses occur during MOSFET turn-on and turn-off transitions due to overlap of voltage and current. The total switching loss Psw is:
where tr and tf are the rise and fall times of the MOSFET, and fsw is the switching frequency.
Magnetic Losses
Core losses in the transformer arise from hysteresis and eddy currents. The Steinmetz equation models core loss Pcore:
where Kh, α, and β are material-dependent coefficients, B is the peak flux density, and Vcore is the core volume.
Winding losses due to skin and proximity effects are approximated by:
where RAC is the frequency-dependent AC resistance of the windings.
Parasitic Losses
Parasitic capacitance (Coss) of the MOSFET contributes to additional losses during switching:
Leakage inductance in the transformer also leads to energy loss, typically dissipated in a snubber circuit.
Practical Efficiency Optimization
To maximize efficiency:
- Select MOSFETs with low RDS(on) and fast switching characteristics.
- Use Schottky diodes for reduced VF in low-voltage outputs.
- Optimize transformer design to minimize leakage inductance and core losses.
- Balance switching frequency to reduce switching losses while maintaining acceptable magnetic losses.
Modern flyback converters in high-efficiency applications (e.g., USB-PD adapters) achieve efficiencies above 90% through careful component selection and layout optimization.
4.2 Load and Line Regulation
Load and line regulation are critical performance metrics for flyback converters, quantifying their ability to maintain a stable output voltage despite variations in input voltage (line regulation) and load current (load regulation). These parameters directly impact the converter's reliability in applications such as power supplies for medical devices, telecommunications, and industrial automation.
Load Regulation
Load regulation measures the converter's ability to maintain a constant output voltage (Vout) as the load current (Iload) changes. It is expressed as a percentage deviation from the nominal output voltage:
Key factors influencing load regulation include:
- Transformer leakage inductance: Energy stored in leakage inductance reduces efficiency and introduces voltage droop under load.
- Output capacitor ESR: A high equivalent series resistance (ESR) increases ripple voltage, degrading regulation.
- Feedback loop bandwidth: A slow control loop cannot compensate quickly for load transients.
Line Regulation
Line regulation quantifies the converter's response to input voltage (Vin) variations, defined as:
Critical design considerations include:
- Duty cycle limitations: At very high or low input voltages, the converter may hit duty cycle limits (Dmin or Dmax), causing loss of regulation.
- Input filter design: Poorly designed input filters can introduce instability or excessive voltage drop.
- Control method: Peak current-mode control inherently improves line regulation by compensating for input voltage changes.
Practical Design Trade-offs
Optimizing load and line regulation often involves trade-offs with other performance metrics:
- Efficiency vs. regulation: Tight regulation may require higher switching frequencies, increasing switching losses.
- Component selection: Low-ESR capacitors and high-permeability transformer cores improve regulation but increase cost.
- Control complexity: Advanced control techniques like adaptive voltage positioning (AVP) can enhance regulation but add design complexity.
Measurement and Validation
Accurate measurement of regulation parameters requires:
- Precision instrumentation: High-resolution oscilloscopes and differential probes to capture small voltage deviations.
- Dynamic load testing: Programmable electronic loads to simulate real-world load steps.
- Statistical analysis: Repeated measurements to account for noise and component tolerances.
For example, a well-designed flyback converter targeting industrial applications might achieve:
- Load regulation: ±1% for load currents ranging from 10% to 100% of full load.
- Line regulation: ±0.5% for input voltages varying ±20% from nominal.
4.3 EMI Considerations and Mitigation
Sources of EMI in Flyback Converters
Flyback converters generate electromagnetic interference (EMI) due to high-frequency switching and abrupt current transitions. The primary sources include:
- Switching node ringing caused by parasitic inductance and capacitance during MOSFET turn-off.
- Diode reverse recovery in the output rectifier, producing high-frequency oscillations.
- Transformer leakage inductance interacting with MOSFET output capacitance, leading to voltage spikes.
- Common-mode noise from capacitive coupling between primary and secondary windings.
Conducted vs. Radiated EMI
EMI manifests in two forms:
- Conducted EMI propagates through power and ground traces, measurable up to 30 MHz. It is governed by standards like CISPR 22 and FCC Part 15.
- Radiated EMI couples through air at frequencies above 30 MHz, influenced by loop areas and high di/dt paths.
Mathematical Modeling of Switching Noise
The voltage spike (Vspike) due to leakage inductance (Llk) and switching current (Ipk) is given by:
where Coss is the MOSFET output capacitance. The resonant frequency of the ringing is:
Mitigation Techniques
Snubber Circuits
An RC snubber suppresses voltage spikes by dissipating energy in the resistor. The optimal snubber values are:
Transformer Design
- Use interleaved windings to reduce leakage inductance.
- Add a Faraday shield between primary and secondary to block common-mode noise.
Layout Strategies
- Minimize high di/dt loop areas (e.g., input capacitor-to-transformer path).
- Use ground planes to reduce radiated emissions.
- Route sensitive traces away from switching nodes.
Filtering Solutions
A two-stage LC filter attenuates conducted EMI. The corner frequency should be at least one decade below the switching frequency:
Compliance Testing
Pre-compliance measurements should include:
- Line impedance stabilization network (LISN) tests for conducted emissions.
- Near-field probes to identify hot spots of radiated EMI.
- Time-domain analysis of switching waveforms using a high-bandwidth oscilloscope.
5. Key Research Papers and Articles
5.1 Key Research Papers and Articles
- How to Design an Isolated Flyback Converter Using LM5157x/LM5158x — MOSFET. The commonly supported configurations include Boost, Flyback and SEPIC topologies. This report focuses on designing the LM5157x/LM5158x as a primary side regulated (PSR) flyback converter. The design procedure is generic on selecting suitable components of the PSR flyback converter for the given application specification.
- Analysis and Design of Multioutput Flyback Converter - Chalmers — Analysis and Design of Multioutput Flyback Converter Master's thesis 2016:ENM ABDI AHMED ABDULLAHI KOSAR Department of Energy & Environment Division of Electric Power Engineering ... ower electronic converters is a common object in today's electronic world and for a very good reason. With quite a bit of interest in smaller sized consumer
- PDF Design and Development of Flyback Converter - ResearchGate — Certified that the major project titled 'Design and development of Flyback converter Topology ' is carried out by T.Vignesh Nayak (1RV14EE055) who is bona-fide student of R.V College of ...
- Modeling and Analysis of the Fractional-Order Flyback Converter in ... — In order to obtain more realistic characteristics of the converter, a fractional-order inductor and capacitor are used in the modeling of power electronic converters. However, few researches focus on power electronic converters with a fractional-order mutual inductance. This paper introduces a fractional-order flyback converter with a fractional-order mutual inductance and a fractional-order ...
- PDF Design and Implementation of Flyback Boost Pfc for Improving ... - Ijcrt — IJCRT22A6319 International Journal of Creative Research Thoughts (IJCRT) www.ijcrt.org 681c 4. PROPOSED SYSTEM The development of new families of Boost flyback converter topologies used in the design of dc-dc and ac-dc converters with active power factor corrections (PFC's). The goal is to design high-efficiency and
- (PDF) Design and implementation of flyback MPPT converter for PV ... — Flyback converter is good solution for MPPT tracking for PV-modules up to 100-150 W with galvanic decoupling. The problem of designing of this type of converter is that most of design guides and ...
- PDF Design equations of high-power-factor flyback ... - STMicroelectronics — flyback converter can assume have been identified. They are illustrated in fig. 1. Configurations a) and b) are basically conventional flyback converters. The former works in TM (Transi-tion Mode, i.e. on the boundary between continuous and discontinuous inductor current mode), therefore at a frequency depending on both input voltage and output ...
- (Pdf) Design of A Multifunctional Flyback Dc-dc Converter With Current ... — A power electronic converter (either DC/DC or DC/AC) is needed to interface the PV array with the load/grid. In this paper, a modified interleaved-type step-up DC-DC flyback converter is presented for a PV application. The topology is based on a multi-winding flyback converter with N parallel connected inputs and a single output.
- PDF FLYING CAPACITOR MULTILEVEL FLYBACK CONVERTER - University of Pittsburgh — flying capacitor multilevel flyback converter (FCMFC) can have flyback conver. M ters in series at the output, with each flyback having . voltage stages (N-1 SDC stages). Each flyback . N transformer has a turns ratio of n. The most basic pulsed power FCMFC, a 2x3 (M. x. N), is shown in . Figure 3.1. with a single SDC stage outlined in red.
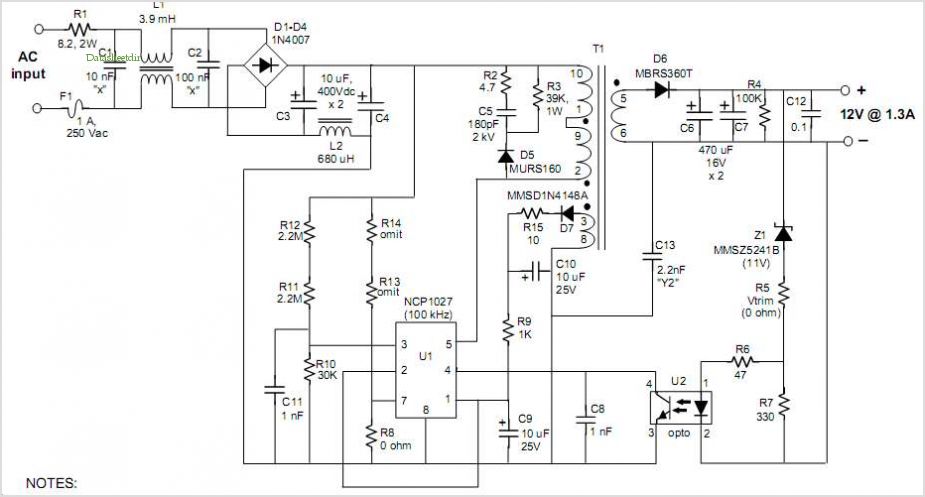
- A Novel Feedback Linearisation Control of Flyback Converter - Sciendo — 2. Operation Principle of Flyback Converter The circuit diagram of the flyback converter is shown in Figure 1. The circuit includes the high-frequency transformer, the switching element (which is more often a metal-oxide-semiconductor field-effect transistor [MOSFET]), the output diode (D), and the capacitor (C).
5.2 Recommended Books and Manuals
- PDF Application Note Hybrid-flyback converter design with XDPS2201 — Hybrid-flyback converter design with XDP™ digital power XDPS2201 . 1 Introduction. Design Guide 3 V1.0 2021-03-01. Chapter 2. Chapter 3. Chapter 4. Chapter 5. Chapter 6. Chapter 7. Chapter 8. Chapter 9. 2 HFB topology and operating principle. 2.1 Hybrid-flyback topology. Figure 1 shows the HFB converter main stage.
- How to Design an Isolated Flyback Converter Using LM5157x/LM5158x — MOSFET. The commonly supported configurations include Boost, Flyback and SEPIC topologies. This report focuses on designing the LM5157x/LM5158x as a primary side regulated (PSR) flyback converter. The design procedure is generic on selecting suitable components of the PSR flyback converter for the given application specification.
- PDF Principles of Power Electronics - Cambridge University Press & Assessment — 7.3 Dual Active-Bridge Converter 150 7.4 Flyback Converter 153 7.5 Other PWM Isolated Converters 154 7.6 Effects of Transformer Leakage Inductance 155 7.7 Converters with Multiple Outputs 158 Notes and Bibliography 158 Problems 159 8 Single-Phase Switched-Mode DC/AC Converters 167 8.1 Basic Variable-Frequency Bridge Converter 167 8.2 Harmonic ...
- PDF Analysis and Design of Multioutput Flyback Converter — Analysis and Design of Multioutput Flyback Converter A study For A Lab Upgrade on the Flyback converter assignment at Chalmers Elteknik Master's thesis in Electric Power Engineering ... ower electronic converters is a common object in today's electronic world and for a very good reason. With quite a bit of interest in smaller sized consumer
- Issa Batarseh, Ahmad Harb - Power Electronics - Circuit Analysis and ... — The objective of this textbook is to provide students with the ability to analyze and design power electronic switching circuits used in ... 303 5.4.1 Single-Ended Flyback Converter ... Continuity in the development of power electronic converter topologies to attain further size and weight reduction with increased efficiency and ...
- PDF Flyback Converters,Active Clamp vs. Hard-Switched Evaluation Board and ... — This user's guide describes the UCC3580EVM flyback converter evaluation board for comparing an active-clamp configuration with a hard-switched configuration. The UCC3580EVM is originally configured as an active-clamp flyback converter. Instructions and parts list are included in order to reconfigure the UCC3580EVM as a hard-switched flyback ...
- How to Design a No-Opto Flyback Converter with Secondary-Side ... - Analog — The output capacitor is selected to limit the output voltage dip to 3% of output voltage for a 50% load step of the rated output current, using the equations below. The recommended bandwidth for the MAX17690-based converter is between f SW /20 and f SW /40. For the present design, the bandwidth is selected as 7kHz.
- PDF Design Guide Fifth-generation fixed-frequency design guide — Design Guide Please read the Important Notice and Warnings at the end of this document V 1.1 ... This document is a design guide for a fixed-frequency flyback converter using Infineon's newest fifth-generation fixed-frequency oolS T™, I5ARxxxxBZS, which offer high-efficiency, low-standby power with ... The recommended typical value for R ...
- PDF AN-556Introduction to Power Supplies - Texas Instruments — 5.5 FLYBACK CONVERTER The three previous regulators are suitable for low voltage control when no electrical isolation is required. However in off-lineswitchers operating from 110V/220V mains, electrical isolation is an absolute must. This is achieved by using a transformer in place of the inductor. The flyback converter shown in Figure 8
- PDF Fairchild Reference Design - Arrow Electronics — Fairchild Reference Design This user guide supports the reference design for a dual-switch flyback solution using the FAN6920MR, FAN7382, and FAN6204. It should be used in conjunction with the product datasheets as well as Fairchild's application notes and technical support team. Please visit Fairchild's website at www.fairchildsemi.com. 1.
5.3 Online Resources and Tools
- PDF 5th Generation Fixed-Frequency Design Guide - Infineon Technologies — Design Guide 3 of 50 Revision 2.1 2019-07-24 5th Generation Fixed-Frequency Design Guide Design Guide - ICE5xSAG and ICE5xRxxxxAG Abstract 1 Abstract This design guide for a fixed-frequency Flyback converter using Infineon's newest fifth-generation fixed-frequency PWM controller, ICE5xSAG, and oolST™, I5xRxxxxA.
- PDF Application Note Hybrid-flyback converter design with XDPS2201 — XDPS2201, converter main stage design, parametrization via .dp vision tool and PCB layout hints. Intended audience Design engineers of power supply with high performance and ultrahigh power density. DG_2009_PL21_2010_113112 Design Guide Please read the Important Notice and Warnings at the end of this document V1.0 www.infineon.com 2021-03-01
- How to Design an Isolated Flyback Using LM5155 (Rev. A) - Texas Instruments — This design guide follows typical design procedures and calculations to implement an isolated nonsynchronous flyback controller operating in continuous conduction mode. The design example uses an unregulated 24V rail (18V-36V) to produce a regulated 5 V of up to 4 A load current. A non-isolated auxiliary winding of 10V is
- Designing an Isolated Buck Converter using the LMR38020 - Texas Instruments — Figure 5-3. Steady State When VIN=16 V, IOUT1=0.4 A, IOUT2=IOUT3=0.1 A.....9 Figure 5-4. Steady State When VIN=60 V, IOUT1=0.4 A, IOUT2=IOUT3=0.1 A ... Flyback converter design has to employ either an opto-coupler or an auxiliary winding as the feedback circuit for output regulation. The loop compensation becomes difficult and sometimes
- AP1682E (Isolated Flyback Design) Calculator - Version 1.6 — AP1682E-Calculator-Isolated-Flyback-Design-1 - Free download as Excel Spreadsheet (.xls), PDF File (.pdf), Text File (.txt) or read online for free. This document provides instructions and calculations for designing an isolated flyback converter. It includes inputting electrical parameters, transformer turns ratio, inductance value, and other component values to size the converter design.
- PDF Design Guide Fifth-generation fixed-frequency design guide — Design Guide Please read the Important Notice and Warnings at the end of this document V 1.1 ... Design guide - ICE5ARxxxxBZS About this document Scope and purpose This document is a design guide for a fixed-frequency flyback converter using Infineon's newest fifth-generation fixed-frequency oolS T™, I5ARxxxxBZS, which offer high-efficiency ...
- PDF Analysis and Design of Multioutput Flyback Converter — ower electronic converters is a common object in today's electronic world and for a very good reason. With quite a bit of interest in smaller sized consumer products and energy e ciency, there is a need for power supplies to adapt to these needs. The evolution of power supplies, as does many other electronic
- Solved Problem 5.3 (25 points) Consider the flyback - Chegg — Answer to Problem 5.3 (25 points) Consider the flyback
- Flyback Converter Calculator — Now that we know the flyback converter design , we can approach the equations behind it. The key parameters that we can compute are the duty cycle, the peak current, and the inductance of the primary and secondary sides.. The duty cycle represents the fraction of one switching period during which the switching device Q 1 Q_1 Q 1 is turned on.It determines how long energy is stored in the ...
- Simple EMI Filter Design for Flyback Converter — To design a input filter you have to have an idea of the problem your trying to solve so you would need to define the following parameters. 1. Amplitude of Lowest Problem Frequency 2. Amplitude required to achieve compliance. These 2 things will allow you to calculate the required attenuation and thus select the correct filter topology.