Infrared Communication Systems

1. Principles of Infrared Transmission

Principles of Infrared Transmission

Electromagnetic Spectrum and Infrared Wavelengths

Infrared (IR) radiation occupies the electromagnetic spectrum between visible light and microwaves, with wavelengths ranging from 700 nm to 1 mm. For communication systems, the near-infrared (NIR) region (700–1400 nm) is most commonly used due to its compatibility with semiconductor materials like silicon and gallium arsenide. The energy of an IR photon is given by:

$$ E = h \nu = \frac{hc}{\lambda} $$

where h is Planck’s constant (6.626 × 10−34 J·s), c is the speed of light (3 × 108 m/s), and λ is the wavelength. At 850 nm, for example, the photon energy is approximately 1.46 eV.

Modulation Techniques

IR communication relies on modulating the intensity of the infrared beam to encode data. Common modulation schemes include:

The choice of modulation affects bandwidth efficiency and noise immunity. For instance, PPM offers better power efficiency but requires precise synchronization.

Link Budget Analysis

The performance of an IR communication link is governed by the link budget, which accounts for transmitted power, path loss, and receiver sensitivity. The received power Pr is derived from the Friis transmission equation:

$$ P_r = P_t G_t G_r \left( \frac{\lambda}{4 \pi d} \right)^2 $$

where Pt is transmitted power, Gt and Gr are the gains of the transmitter and receiver antennas, and d is the distance between them. Atmospheric absorption and scattering further attenuate the signal, particularly in humid environments.

Noise Sources and Signal-to-Noise Ratio

Dominant noise sources in IR systems include:

The signal-to-noise ratio (SNR) is critical for determining the bit error rate (BER) and is expressed as:

$$ \text{SNR} = \frac{(R P_r)^2}{2q (R P_r + I_{dark}) B + 4kTB / R_L} $$

where R is the responsivity of the photodetector (A/W), q is the electron charge, Idark is the dark current, B is the bandwidth, k is Boltzmann’s constant, T is temperature, and RL is the load resistance.

Practical Considerations

IR communication systems face challenges such as:

Applications range from remote controls (using 940 nm LEDs) to high-speed free-space optical links (e.g., 1550 nm lasers for last-mile connectivity).

1.2 Infrared Spectrum and Wavelengths

The infrared (IR) spectrum occupies the electromagnetic region between visible light and microwaves, typically spanning wavelengths from 700 nanometers (nm) to 1 millimeter (mm). This range is subdivided into three primary bands based on atmospheric absorption characteristics and technological applications:

Near-Infrared (NIR)

Ranging from 700 nm to 1400 nm, NIR is closest to visible light and exhibits minimal atmospheric absorption. Its photon energy (E) can be calculated using Planck's relation:

$$ E = \frac{hc}{\lambda} $$

where h is Planck's constant (6.626 × 10-34 J·s), c is the speed of light (3 × 108 m/s), and λ is the wavelength. For λ = 1000 nm:

$$ E = \frac{(6.626 \times 10^{-34})(3 \times 10^8)}{1000 \times 10^{-9}} \approx 1.99 \times 10^{-19} \text{ J} $$

Mid-Infrared (MIR)

Extending from 1400 nm to 3000 nm, MIR overlaps with the vibrational modes of many molecules, making it critical for spectroscopic applications. The Wien's displacement law relates peak emission wavelength (λmax) to blackbody temperature (T):

$$ \lambda_{max} = \frac{b}{T} $$

where b = 2.898 × 10-3 m·K. A human body at 310 K emits maximally at:

$$ \lambda_{max} = \frac{2.898 \times 10^{-3}}{310} \approx 9350 \text{ nm} $$

Far-Infrared (FIR)

Covering 3000 nm to 1 mm, FIR interacts strongly with rotational molecular states. The propagation loss (α) in dB/km through atmosphere follows the Beer-Lambert law:

$$ \alpha = 10 \log_{10}\left(\frac{I_0}{I}\right) \cdot \frac{1}{L} $$

where I0 and I are initial and transmitted intensities, and L is path length. Water vapor causes attenuation peaks at 2.7 μm, 6.3 μm, and 12-25 μm.

Atmospheric Transmission Windows

Three primary windows enable practical IR communication:

The transmittance (τ) through 1 km of standard atmosphere at sea level drops below 50% outside these windows due to H2O and CO2 absorption bands.

Material Interactions

The complex refractive index ñ = n + iκ governs IR behavior in materials, where n is the refractive index and κ the extinction coefficient. The penetration depth (δ) for intensity decay to 1/e is:

$$ \delta = \frac{\lambda}{4\pi\kappa} $$

For silicon at λ = 1500 nm (κ ≈ 0.01), δ ≈ 12 μm, enabling photodetector design optimization.

Infrared Spectrum Bands and Atmospheric Transmission A spectrum chart showing infrared subdivisions (NIR, MIR, FIR), atmospheric transmission windows, and absorption peaks for H2O and CO2. Wavelength (μm) 0.7 1.4 3 5 8 14 NIR 0.7-1.4μm MIR 3-5μm FIR 8-14μm Transmission Window H₂O CO₂ NIR (Near Infrared) MIR (Mid Infrared) FIR (Far Infrared) Transmission Windows Absorption Peaks
Diagram Description: The diagram would show the infrared spectrum subdivisions with wavelength ranges, atmospheric transmission windows, and absorption bands.

1.3 Modulation Techniques in IR Communication

Fundamentals of Modulation in IR Systems

Infrared communication relies on modulating an optical carrier signal to encode information. Unlike RF systems, IR typically operates in the near-infrared spectrum (700 nm–1 mm), where intensity modulation is more practical than phase or frequency modulation due to detector characteristics. The baseband signal m(t) modulates the intensity of an IR LED or laser diode, producing the transmitted signal x(t):

$$ x(t) = P_0 \left[1 + k m(t)\right] \cos(2\pi f_c t) $$

where P0 is the average optical power, k is the modulation index (0 < k ≤ 1), and fc is the carrier frequency (typically 30–60 kHz for consumer IR). The receiver uses a photodiode with transimpedance amplification to convert the optical signal back to an electrical waveform.

Pulse Modulation Schemes

Three primary pulse-based modulation techniques dominate IR communication:

Carrier-Based Modulation

For noise immunity, most IR systems employ subcarrier modulation, where the baseband signal modulates an intermediate frequency (IF) carrier before driving the LED:

$$ x(t) = P_0 \left[1 + k \cdot m(t) \cdot \cos(2\pi f_{sc} t)\right] $$

Common subcarrier frequencies range from 36 kHz (TV remotes) to 455 kHz (high-speed data links). The receiver uses bandpass filtering centered at fsc to reject ambient light noise.

Amplitude Shift Keying (ASK)

The simplest digital modulation scheme, where:

$$ x(t) = \begin{cases} P_0 \cos(2\pi f_c t) & \text{for bit '1'} \\ 0 & \text{for bit '0'} \end{cases} $$

Used in low-cost systems but susceptible to interference from fluorescent lights and sunlight.

Frequency Shift Keying (FSK)

Less common in IR due to detector limitations, but employed in some secure communication systems:

$$ x(t) = P_0 \cos\left(2\pi (f_c + \Delta f \cdot m(t)) t\right) $$

where Δf is the frequency deviation. Requires more complex receivers with frequency discrimination.

Advanced Techniques

For high-data-rate applications (>1 Mbps), quadrature amplitude modulation (QAM) and orthogonal frequency-division multiplexing (OFDM) are implemented in IR:

Practical Implementation Considerations

The choice of modulation involves trade-offs between:

Modern IR transceivers (e.g., Vishay TFDU4101) integrate modulation/demodulation circuits, handling carrier generation and synchronization automatically.

Comparison of IR Modulation Techniques Time-domain waveforms for PWM, PPM, PCM, ASK, and FSK signals, showing pulse shapes, durations, and key modulation parameters. Time PWM (Pulse Width Modulation) 1 0 1 0 1 0 1 0 PPM (Pulse Position Modulation) 1 0 1 0 1 0 1 0 PCM (Pulse Code Modulation) 1010 1100 1010 1100 ASK (Amplitude Shift Keying) 1 0 1 0 0 1 1 1 FSK (Frequency Shift Keying) 1 0 1 0 1 0 1 0 Modulation Indices: k (PWM), Δf (FSK)
Diagram Description: The section describes multiple modulation techniques with specific timing relationships and signal transformations that are inherently visual.

2. Infrared Transmitters: LEDs and Laser Diodes

Infrared Transmitters: LEDs and Laser Diodes

Infrared Light-Emitting Diodes (IR LEDs)

Infrared LEDs are semiconductor devices that emit incoherent light in the 700 nm to 1 mm wavelength range when forward-biased. The spectral output is governed by the bandgap energy Eg of the semiconductor material, typically gallium arsenide (GaAs) or aluminum gallium arsenide (AlGaAs). The peak emission wavelength λp is given by:

$$ \lambda_p = \frac{hc}{E_g} $$

where h is Planck's constant and c is the speed of light. For GaAs (Eg ≈ 1.42 eV), this yields λp ≈ 870 nm. The optical power output Po relates to the drive current IF as:

$$ P_o = \eta_e \cdot \frac{hc}{\lambda} \cdot \frac{I_F}{e} $$

where ηe is the external quantum efficiency and e is the electron charge. Practical IR LEDs achieve radiant intensities of 10–100 mW/sr at 100 mA drive currents.

Infrared Laser Diodes

Laser diodes produce coherent, monochromatic light through stimulated emission in a Fabry-Pérot cavity. The threshold current density Jth for lasing is derived from the gain condition:

$$ \Gamma g_{th} = \alpha_i + \frac{1}{2L} \ln\left(\frac{1}{R_1 R_2}\right) $$

where Γ is the optical confinement factor, gth is the threshold gain, αi is the internal loss, L is the cavity length, and R1, R2 are facet reflectivities. Common infrared laser diodes use InGaAsP/InP heterostructures emitting at 1310 nm or 1550 nm for fiber-optic applications.

Modulation Characteristics

Both devices can be intensity-modulated for data transmission. The modulation bandwidth f3dB of LEDs is limited by carrier recombination:

$$ f_{3dB} = \frac{1}{2\pi\tau_r} $$

where τr is the minority carrier lifetime (typically 1–10 ns, yielding 16–160 MHz bandwidth). Laser diodes exhibit relaxation oscillations with a resonance frequency:

$$ f_r = \frac{1}{2\pi}\sqrt{\frac{v_g a \eta_i (I - I_{th})}{q V_p}} $$

where vg is the group velocity, a is the differential gain, ηi is the internal quantum efficiency, and Vp is the active layer volume.

Thermal Considerations

The wavelength temperature coefficient dλ/dT differs significantly between devices:

Thermal resistance Rth must be minimized to prevent thermal runaway in laser diodes, where the threshold current follows:

$$ I_{th}(T) = I_{th0} e^{T/T_0} $$

with T0 being the characteristic temperature (50–100 K for InGaAsP lasers).

Practical Implementation

Drive circuits require:

Optimal coupling efficiency is achieved through aspheric lenses (LEDs) or graded-index lenses (lasers) to match the emission patterns:

IR LED vs. Laser Diode Emission Patterns and Modulation Comparative diagram showing IR LED Lambertian emission and Laser Gaussian beam patterns with corresponding intensity modulation waveforms and drive current signals. IR LED θ (FWHM) Lambertian Emission Intensity Modulation P₀ I_F Laser Diode θ (FWHM) Gaussian Beam Intensity Modulation P₀ I_F Drive Current Signals fᵣ τᵣ fᵣ τᵣ λₚ: Peak Wavelength
Diagram Description: The section discusses emission patterns (Lambertian vs. Gaussian) and modulation characteristics that are inherently spatial and temporal.

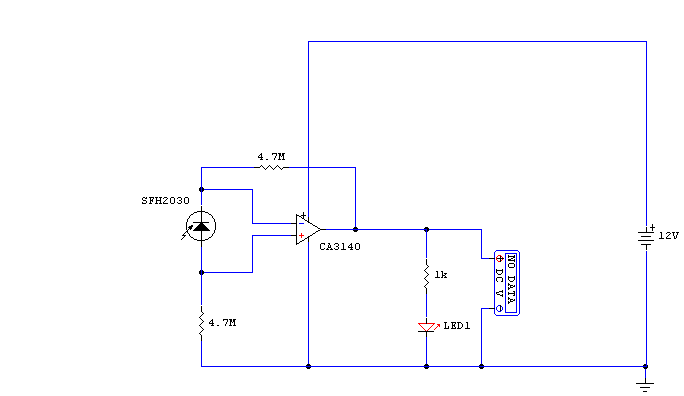
2.2 Infrared Receivers: Photodiodes and Phototransistors

Photodiodes in Infrared Detection

Photodiodes are semiconductor devices that convert incident infrared (IR) radiation into an electrical current through the photoelectric effect. When photons with sufficient energy strike the diode’s depletion region, electron-hole pairs are generated, producing a photocurrent proportional to the incident optical power. The responsivity R of a photodiode is defined as:

$$ R = \frac{I_p}{P_{opt}} $$

where Ip is the photocurrent and Popt is the incident optical power. For typical silicon photodiodes in the near-IR range (700–1100 nm), R ranges from 0.5 to 0.7 A/W.

Key Performance Parameters

$$ \eta = \frac{hc \cdot R}{e \cdot \lambda} $$

where h is Planck’s constant, c is the speed of light, e is the electron charge, and λ is the wavelength.

Phototransistors for Enhanced Sensitivity

Phototransistors amplify the photocurrent by leveraging the transistor’s current gain (β). Unlike photodiodes, they operate in active mode, with the base current generated by photon absorption. The collector current IC is:

$$ I_C = \beta \cdot I_p $$

This makes phototransistors suitable for low-intensity IR signals but at the cost of slower response times (microseconds) due to charge storage effects.

Trade-offs Between Photodiodes and Phototransistors

Practical Considerations in Receiver Design

To minimize noise in IR receivers:

Applications in Modern Systems

Photodiodes dominate high-speed IR communication (e.g., fiber optics, LiDAR), while phototransistors are preferred in proximity sensors and remote controls due to their integrated gain. Emerging technologies like quantum dot photodiodes are pushing detectivity limits beyond traditional InGaAs systems.

Photodiode vs. Phototransistor Operation A side-by-side comparison of photodiode and phototransistor operation, showing internal carrier flow and amplification mechanisms under incident IR photons. Photodiode vs. Phototransistor Operation Photodiode Depletion Region P N IR Photon Photocurrent (Iₚ) Phototransistor Emitter (E) Base (B) Collector (C) IR Photon Iₚ (Base Current) I꜀ (Collector Current) β (Current Gain) Quantum Efficiency (η) Dark Current Current Gain (β = I꜀/Iₚ)
Diagram Description: A diagram would show the structural and operational differences between photodiodes and phototransistors, including their internal carrier flow and amplification mechanisms.

2.3 Signal Conditioning Circuits

Signal conditioning circuits are critical in infrared (IR) communication systems to ensure optimal signal integrity, noise immunity, and compatibility with subsequent processing stages. These circuits typically include amplification, filtering, and modulation/demodulation stages to enhance the weak IR signals received by photodiodes or phototransistors.

Amplification and Transimpedance Design

The primary challenge in IR signal conditioning is amplifying the weak photocurrent generated by the detector while minimizing noise. A transimpedance amplifier (TIA) is commonly employed, converting the photodiode current into a voltage signal. The feedback resistor Rf and capacitor Cf determine the gain and bandwidth:

$$ V_{out} = -I_{ph} \cdot R_f $$

where Iph is the photodiode current. The bandwidth is constrained by the amplifier's gain-bandwidth product (GBWP) and the photodiode capacitance Cd:

$$ f_{-3dB} = \frac{1}{2\pi R_f (C_d + C_f)} $$

To minimize noise, a low-noise operational amplifier (e.g., JFET-input) and careful PCB layout techniques (e.g., guarding, shielding) are essential.

Bandpass Filtering for Noise Reduction

IR communication systems often operate in environments with ambient IR interference (e.g., sunlight, incandescent lighting). A bandpass filter centered at the carrier frequency (typically 38 kHz for consumer IR) suppresses out-of-band noise. A multiple feedback (MFB) bandpass filter provides a sharp roll-off:

$$ f_0 = \frac{1}{2\pi \sqrt{R_1 R_2 C_1 C_2}} $$ $$ Q = \frac{1}{2} \sqrt{\frac{R_2}{R_1}} $$

where f0 is the center frequency and Q is the quality factor. Higher Q improves selectivity but reduces bandwidth.

Demodulation and Threshold Detection

For pulse-modulated IR signals (e.g., RC-5, NEC protocols), an envelope detector followed by a comparator extracts the digital signal. The comparator's hysteresis prevents noise-induced false triggering:

$$ V_{th} = \pm \frac{R_2}{R_1 + R_2} V_{ref} $$

where Vth is the threshold voltage. A Schmitt trigger configuration ensures clean digital output even with noisy input.

Practical Implementation Considerations

IR Signal Conditioning Block Diagram Block diagram illustrating the signal conditioning stages in an infrared communication system, including photodiode, transimpedance amplifier, bandpass filter, envelope detector, and comparator. Photodiode I_ph TIA R_f, C_f Bandpass Filter f_0, Q Envelope Detector Comparator V_th, V_ref
Diagram Description: The section describes complex circuit interactions (transimpedance amplifier, bandpass filter, demodulation) where spatial relationships and signal transformations are critical.

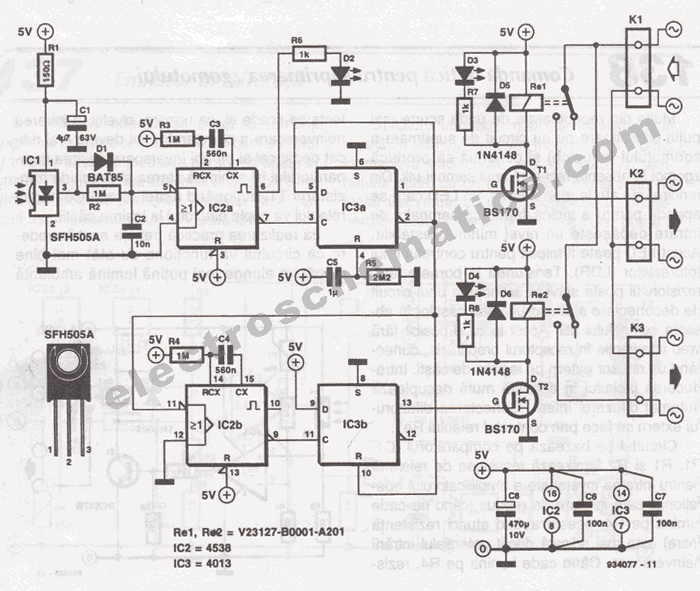
3. Common IR Protocols: RC5, NEC, and SIRC

3.1 Common IR Protocols: RC5, NEC, and SIRC

RC5 Protocol

The RC5 protocol, developed by Philips, is a widely used infrared communication standard for remote control applications. It employs Manchester encoding to ensure robust data transmission with a carrier frequency of 36 kHz. Each RC5 frame consists of 14 bits:

The bit duration is standardized at 1.778 ms, resulting in a total frame time of 25 ms. The Manchester encoding scheme ensures synchronization by representing logic '1' as a high-to-low transition and logic '0' as a low-to-high transition at the midpoint of the bit period.

$$ T_{bit} = \frac{1}{36 \times 10^3} \times 64 \approx 1.778 \text{ ms} $$

NEC Protocol

The NEC protocol is another prevalent IR standard, characterized by its pulse distance modulation. It uses a 38 kHz carrier and encodes data with pulse bursts of varying lengths. A complete NEC frame comprises:

Logical '0' is represented by a 562.5 µs pulse followed by a 562.5 µs space, while logical '1' consists of a 562.5 µs pulse followed by a 1.6875 ms space. The protocol's redundancy in transmitting inverted address and command bytes enhances reliability.

Sony SIRC Protocol

The Sony SIRC (Serial Infrared Remote Control) protocol is a simpler yet efficient standard with variable command lengths (12, 15, or 20 bits). It operates at a carrier frequency of 40 kHz and uses pulse width encoding:

Each bit begins with a 600 µs pulse burst. A logical '1' is followed by a 1.2 ms space, while a logical '0' is followed by a 600 µs space. The total frame time depends on the number of '1's and '0's transmitted, making SIRC less deterministic than RC5 or NEC.

Comparative Analysis

The three protocols differ in modulation techniques, error handling, and efficiency:

In practice, NEC is favored for consumer electronics due to its balance of robustness and simplicity, while RC5 remains prevalent in professional systems requiring toggle bit functionality.

IR Protocol Timing Comparison Time-aligned waveform comparison of RC5, NEC, and SIRC infrared communication protocols showing bit encoding, start/stop markers, and spaces. Time (ms) Voltage 1.778 3.556 5.334 7.112 8.89 10.668 12.446 RC5 Protocol Start 1.778ms 1.778ms NEC Protocol 9ms 4.5ms 562.5µs SIRC Protocol 600µs 1.2ms 600µs Legend RC5 NEC SIRC
Diagram Description: The section describes complex timing and encoding schemes (Manchester, pulse distance, pulse width) that are inherently visual and require waveform representation to fully grasp.

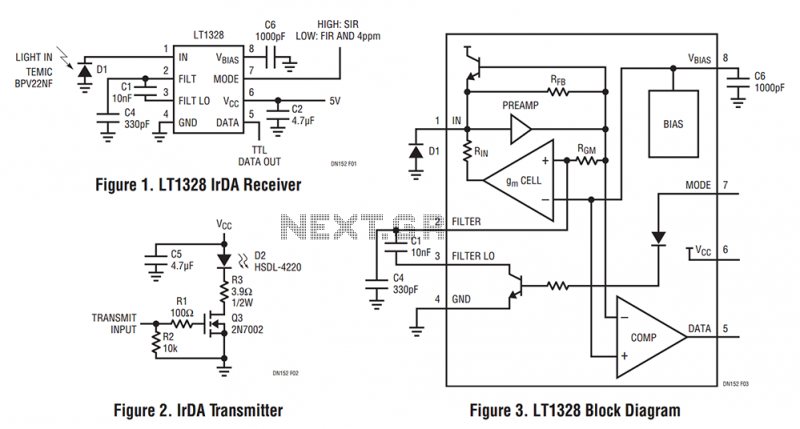
3.2 IR Data Association (IrDA) Standards

The Infrared Data Association (IrDA) standards define a suite of protocols for short-range, line-of-sight infrared communication. Developed in the 1990s, these standards enable reliable data exchange between devices such as laptops, PDAs, printers, and mobile phones. IrDA operates in the near-infrared spectrum (850–900 nm), leveraging pulse-position modulation (PPM) and asynchronous serial communication.

Physical Layer Specifications

IrDA defines multiple physical layer (PHY) standards, each optimized for specific data rates and power constraints:

The transmission range is typically limited to 1 meter, with a half-angle divergence of 15–30 degrees to minimize interference. The link budget is governed by the inverse-square law:

$$ P_r = P_t \cdot \left( \frac{\lambda}{4 \pi d} \right)^2 \cdot \eta_t \eta_r $$

where \(P_r\) is received power, \(P_t\) is transmitted power, \(\lambda\) is wavelength, \(d\) is distance, and \(\eta_t, \eta_r\) are transmitter/receiver efficiencies.

Protocol Stack Architecture

IrDA's layered protocol stack includes:

Devices negotiate parameters during the Discovery Phase using a 500 ms sniff interval and 8–10 discovery slots. The Normal Connect Phase employs a 1.6 μs guard time between bytes to prevent overlap.

Error Handling and Performance

IrDA uses CRC-16 for error detection and selective repeat ARQ for retransmission. The bit error rate (BER) is approximated by:

$$ \text{BER} = \frac{1}{2} \text{erfc} \left( \sqrt{\frac{E_b}{N_0}} \right) $$

where \(E_b/N_0\) is the energy-per-bit-to-noise ratio. Typical implementations achieve a BER of \(10^{-9}\) at 1 meter.

Modern Applications and Limitations

Despite being supplanted by Bluetooth and Wi-Fi, IrDA remains relevant in:

Key limitations include susceptibility to ambient light noise and strict alignment requirements. Recent advancements like IrDA Control optimize the standard for low-power remote control applications.

3.3 Error Detection and Correction Methods

Infrared communication systems are susceptible to noise, interference, and signal degradation, necessitating robust error detection and correction techniques. These methods ensure data integrity by identifying and rectifying bit errors introduced during transmission.

Parity Check

The simplest form of error detection is the parity check, where an additional bit (parity bit) is appended to a data word to ensure an even or odd number of set bits. For a data word D of length n, the parity bit P is computed as:

$$ P = D_0 \oplus D_1 \oplus \dots \oplus D_{n-1} $$

If a single-bit error occurs, the receiver detects a parity mismatch. However, this method fails for even-numbered bit errors and does not correct errors.

Checksum

A checksum extends the parity concept by summing all data words and transmitting the result. The receiver recomputes the checksum and compares it with the received value. While computationally efficient, checksums are vulnerable to certain error patterns, such as reordered data words.

Cyclic Redundancy Check (CRC)

CRC is a more robust error-detection method using polynomial division. The sender appends a checksum (remainder) derived from dividing the data by a predefined generator polynomial G(x). The receiver performs the same division; a non-zero remainder indicates errors.

$$ R(x) = \text{Data}(x) \cdot x^k \mod G(x) $$

Common CRC polynomials include CRC-16 (x16 + x15 + x2 + 1) and CRC-32, used in Ethernet and ZIP files.

Hamming Codes

Hamming codes enable single-bit error correction and double-bit error detection. For a data word of length k, r parity bits are added such that 2r ≥ k + r + 1. The parity bits are placed at positions that are powers of two (1, 2, 4, etc.), and each covers a specific subset of data bits.

$$ \text{Syndrome} = P_1 \oplus D_3 \oplus D_5 \oplus D_7 $$

The syndrome identifies the erroneous bit position, allowing correction.

Reed-Solomon Codes

For burst errors common in infrared channels, Reed-Solomon (RS) codes are highly effective. RS codes operate on symbols rather than bits, correcting up to t symbol errors where t = (n - k)/2. They are widely used in optical communications, QR codes, and CDs.

$$ n = 2^m - 1 $$

where m is the symbol size in bits.

Automatic Repeat Request (ARQ)

ARQ protocols, such as Stop-and-Wait or Selective Repeat, combine error detection with retransmission requests. The receiver sends an acknowledgment (ACK) for correct frames or a negative acknowledgment (NACK) for corrupted ones, prompting retransmission. ARQ is efficient in low-noise environments but introduces latency.

Forward Error Correction (FEC)

FEC integrates error correction directly into the transmitted data, eliminating the need for retransmissions. Convolutional codes and Turbo codes are advanced FEC techniques used in deep-space communications and 4G/5G networks. The Viterbi algorithm decodes convolutional codes by finding the most likely transmitted sequence.

$$ \text{Code Rate} = \frac{k}{n} $$

where k is the number of information bits and n is the total encoded bits.

Hamming Code Parity Bit Placement and CRC Polynomial Division Diagram showing Hamming code parity bit positions and CRC polynomial division steps for infrared communication systems. Hamming Code Parity Bit Placement 1 2 3 4 5 6 7 P1 P2 P4 Parity Bits Data Bits CRC Polynomial Division Data Bits: 11010011101100 Generator Polynomial: G(x) = x³ + x + 1 Remainder: R(x) = 101
Diagram Description: A diagram would visually demonstrate the spatial arrangement of parity bits in Hamming codes and the polynomial division process in CRC, which are complex to describe textually.

4. Remote Control Systems

4.1 Remote Control Systems

Fundamentals of Infrared Remote Control

Infrared (IR) remote control systems operate by modulating near-infrared light (typically 850–950 nm) to transmit digital commands. The carrier frequency, usually between 36 kHz and 56 kHz, is chosen to minimize interference from ambient light sources. The modulation scheme is typically pulse-width modulation (PWM) or pulse-distance modulation (PDM), with Manchester or RC-5 encoding for robustness.

$$ P_{\text{IR}} = P_0 \cdot \eta_{\text{LED}} \cdot D $$

where PIR is the emitted IR power, P0 is the LED's peak power, ηLED is the electro-optical conversion efficiency, and D is the duty cycle of the modulation.

Signal Encoding Protocols

Common IR protocols include:

The bit duration Tb is derived from the carrier period Tc and the encoding scheme. For NEC:

$$ T_b = \frac{1}{f_c} \cdot N_{\text{cycles}} $$

where Ncycles is the number of carrier cycles per bit (e.g., 16 for logical '0' in NEC).

Receiver Design and Noise Immunity

IR receivers integrate a photodiode, transimpedance amplifier, bandpass filter (centered at the carrier frequency), and demodulator. The signal-to-noise ratio (SNR) is critical:

$$ \text{SNR} = \frac{I_{\text{signal}}^2}{I_{\text{noise}}^2 = \frac{(R \cdot P_{\text{IR}})^2}{4q(I_{\text{dark}} + I_{\text{bg}})B + \frac{4kTB}{R_f}} $$

where R is the photodiode responsivity (A/W), Idark is the dark current, Ibg is background light current, and B is the bandwidth.

Practical Implementation Challenges

Key design considerations include:

Advanced Applications

Modern systems incorporate bidirectional IR (e.g., HDMI-CEC) or hybrid RF/IR solutions for extended range. Machine learning is increasingly used for gesture recognition via IR array sensors.

IR LED Modulated Signal Receiver
IR Remote Control Signal Encoding and Reception Diagram showing IR signal encoding with PWM/PDM modulation and receiver processing stages including photodiode, amplifier, bandpass filter, and demodulator. IR LED PWM Encoding Carrier (36-56 kHz) Photodiode R = Responsivity Amplifier Bandpass Filter Demodulator SNR = ... Received Signal Transmitter Receiver
Diagram Description: The section covers modulation schemes, signal encoding protocols, and receiver design, which are highly visual concepts involving waveforms and signal transformations.

4.2 Short-Range Data Transfer

Operating Principles

Short-range infrared (IR) data transfer relies on modulated near-infrared light (700–1000 nm) for communication over distances typically less than 1 meter. The transmitter encodes data by varying the intensity of an IR LED, while the receiver decodes the signal using a photodiode or phototransistor. The system operates in one of two modes:

Modulation Techniques

To mitigate ambient IR noise, pulse modulation schemes are employed:

$$ P(t) = P_0 \left[1 + m \cdot s(t)\right] \cdot \cos(2\pi f_c t) $$

where P0 is the baseline optical power, m the modulation index (0.7–0.9 for typical systems), s(t) the data signal, and fc the carrier frequency (typically 30–56 kHz for consumer electronics). Common protocols include:

Channel Characteristics

The path loss in IR systems follows an inverse-square law with additional atmospheric attenuation:

$$ L_{path} = 10 \log_{10}\left(\frac{A_r}{(d \cdot \theta)^2}\right) + \alpha d $$

where Ar is the receiver area, d the distance, θ the beam divergence angle, and α the atmospheric attenuation coefficient (~0.1 dB/m in clear air). Multipath dispersion in diffuse systems causes intersymbol interference (ISI), limiting the maximum symbol rate to:

$$ R_{max} \approx \frac{1}{10 \cdot \tau_{rms}} $$

with τrms being the RMS delay spread of the channel.

Practical Implementations

Modern IR transceivers integrate automatic gain control (AGC) and adaptive equalization to combat channel impairments. The IrPHY standard specifies:

Typical applications include:

Error Performance Analysis

The bit error rate (BER) for an OOK-modulated IR link under shot noise follows:

$$ P_e = Q\left(\sqrt{\frac{\eta P_s^2}{2h\nu B(P_s + P_b + P_{dc})}}\right) $$

where η is the detector quantum efficiency, Ps the signal power, hν the photon energy, B the bandwidth, Pb the background radiation power, and Pdc the dark current power. Forward error correction (FEC) codes like Reed-Solomon (255,223) are commonly applied to achieve BER < 10⁻⁹ in commercial systems.

Directed vs. Diffuse IR Communication Modes A side-by-side comparison of directed (line-of-sight) and diffuse (non-line-of-sight) infrared communication modes, showing beam paths and reflection patterns. Directed vs. Diffuse IR Communication Modes Transmitter Receiver Line-of-sight Beam divergence angle Transmitter Receiver Non-line-of-sight Reflection points Legend Direct beam path Reflected beam path Transmitter Receiver
Diagram Description: The diagram would show the difference between directed (line-of-sight) and diffuse (non-line-of-sight) IR communication modes, including beam paths and reflection patterns.

4.3 Industrial and Medical Applications

Industrial Automation and Control

Infrared (IR) communication systems are extensively deployed in industrial environments for wireless data transmission between sensors, actuators, and control units. Unlike radio-frequency (RF) systems, IR avoids electromagnetic interference (EMI) with sensitive industrial equipment. The line-of-sight requirement is often mitigated by using diffuse IR configurations, where signals reflect off surfaces to reach receivers.

$$ P_r = P_t \cdot \left( \frac{\lambda}{4 \pi d} \right)^2 \cdot G_t \cdot G_r \cdot \eta_{\text{atm}} \cdot \eta_{\text{opt}} $$

Here, \(P_r\) is received power, \(P_t\) is transmitted power, \(\lambda\) is wavelength, \(d\) is distance, \(G_t\) and \(G_r\) are antenna gains, and \(\eta_{\text{atm}}\) and \(\eta_{\text{opt}}\) account for atmospheric and optical losses. Industrial IR links typically operate at 850–950 nm for optimal penetration through dust and vapors.

Medical Telemetry and Diagnostics

In medical applications, IR enables non-invasive patient monitoring through pulse oximeters, capnographs, and implantable device telemetry. Near-infrared (NIR) spectroscopy (700–2500 nm) exploits tissue transparency to measure blood oxygenation (\(SpO_2\)) via the Beer-Lambert law:

$$ I = I_0 e^{-\epsilon c l} $$

where \(I\) is transmitted intensity, \(I_0\) is incident intensity, \(\epsilon\) is molar absorptivity, \(c\) is concentration, and \(l\) is path length. IR-based endoscopic capsules transmit real-time imagery at 20–50 Mbps using on-off keying (OOK) modulation.

Case Study: IR in Sterile Environments

Pharmaceutical cleanrooms employ IR data links to maintain sterility by eliminating cable ports. A 2021 study demonstrated a 10-meter IR network achieving 1 Gbps via vertical-cavity surface-emitting lasers (VCSELs) and avalanche photodiodes (APDs), with bit-error rates (BER) below \(10^{-12}\).

Safety and Regulatory Compliance

Industrial IR systems must comply with IEC 62471 for photobiological safety, limiting irradiance to 10 W/m² for prolonged exposure. Medical devices adhere to FDA 21 CFR 1040.10, requiring fail-safe beam termination at >5 mW output.

IR Transmitter IR Receiver

Modern implementations integrate adaptive optics to compensate for misalignment in vibrating machinery, using MEMS-based beam steering with <1 ms latency.

Diffuse IR Communication in Industrial Environments Illustration of diffuse infrared communication showing signal paths reflecting off surfaces to reach the receiver despite obstacles. IR Transmitter IR Receiver Obstacle Diffuse Reflection Paths
Diagram Description: The diagram would physically show the diffuse IR configuration in industrial settings, illustrating how signals reflect off surfaces to reach receivers despite line-of-sight limitations.

5. Range and Line-of-Sight Requirements

5.1 Range and Line-of-Sight Requirements

Infrared (IR) communication systems rely on the propagation of electromagnetic waves in the 700 nm to 1 mm wavelength range, typically operating between 300 GHz and 430 THz. The effective range of such systems is governed by the inverse square law, atmospheric absorption, and the necessity for an unobstructed line-of-sight (LOS) path.

Power Budget and Range Limitations

The maximum achievable range d of an IR communication link is determined by the transmitted power Pt, receiver sensitivity Pr, and the system's optical efficiency. The Friis transmission equation for free-space optical communication is given by:

$$ P_r = P_t \cdot G_t \cdot G_r \cdot \left( \frac{\lambda}{4 \pi d} \right)^2 \cdot \eta_t \cdot \eta_r $$

where:

Atmospheric attenuation further reduces the received power due to scattering and absorption by molecules such as H2O and CO2. The Beer-Lambert law describes this attenuation:

$$ P_r = P_0 \cdot e^{-\alpha d} $$

where α is the attenuation coefficient, which varies with wavelength and environmental conditions.

Line-of-Sight (LOS) Constraints

Unlike radio-frequency (RF) systems, IR communication requires a direct, unobstructed path between transmitter and receiver. Diffraction effects are negligible due to the short wavelength, making non-LOS (NLOS) communication impractical without reflectors or repeaters. The divergence angle θ of the IR beam influences the required alignment precision:

$$ \theta = \frac{2 \lambda}{\pi w_0} $$

where w0 is the beam waist radius. Narrow beams enable longer ranges but demand precise pointing mechanisms.

Practical Considerations

In real-world deployments, IR communication systems face challenges such as:

Advanced modulation techniques (e.g., pulse-position modulation) and error-correcting codes are often employed to mitigate these issues.

Case Study: IRDA Standard

The Infrared Data Association (IrDA) specifies short-range (< 1 m) communication with a half-angle divergence of 15°–30°. This trade-off between range and alignment tolerance makes IrDA suitable for portable devices like smartphones and laptops.

IR Communication Range and LOS Constraints A technical illustration showing the geometric relationship between an IR transmitter and receiver, including beam divergence and atmospheric attenuation effects. Transmitter Pt Receiver Pr d (range) θ Divergence Angle Atmospheric Attenuation (α)
Diagram Description: The diagram would show the geometric relationship between transmitter, receiver, and beam divergence in a line-of-sight scenario, along with atmospheric attenuation effects.

5.2 Ambient Light Interference and Mitigation

Infrared (IR) communication systems are susceptible to ambient light interference, which introduces noise and reduces signal integrity. This interference arises from natural and artificial sources, including sunlight, incandescent bulbs, and fluorescent lighting, all of which emit IR radiation overlapping with the communication band.

Sources of Ambient Light Interference

The primary contributors to ambient IR noise are:

The spectral irradiance of these sources can be modeled using Planck's law for thermal emitters and empirical data for artificial lighting.

Quantifying Interference: Signal-to-Noise Ratio (SNR)

The SNR in an IR communication link is given by:

$$ \text{SNR} = \frac{P_{\text{signal}}}{P_{\text{noise}}} = \frac{\int_{\lambda_1}^{\lambda_2} S(\lambda) \, d\lambda}{\int_{\lambda_1}^{\lambda_2} N(\lambda) \, d\lambda} $$

where:

Mitigation Techniques

1. Optical Filtering

Bandpass optical filters attenuate out-of-band noise while transmitting the desired IR signal. The filter's transmission coefficient T(λ) modifies the SNR as:

$$ \text{SNR}_{\text{filtered}} = \frac{\int_{\lambda_1}^{\lambda_2} S(\lambda) T(\lambda) \, d\lambda}{\int_{\lambda_1}^{\lambda_2} N(\lambda) T(\lambda) \, d\lambda} $$

Common filter types include:

2. Modulation Techniques

High-frequency modulation (e.g., 38–56 kHz) shifts the signal beyond the flicker noise of ambient sources. The receiver uses synchronous detection to reject low-frequency noise:

$$ V_{\text{out}} = \frac{2}{T} \int_0^T s(t) \cdot \text{carrier}(t) \, dt $$

where s(t) is the received signal and carrier(t) is the reference waveform.

3. Adaptive Thresholding

Real-time adjustment of the detection threshold compensates for varying ambient conditions. A feedback loop measures the DC offset from ambient light and subtracts it:

$$ V_{\text{threshold}} = \alpha \cdot \overline{V_{\text{noise}}} + \beta $$

where α and β are empirically determined constants.

Case Study: Sunlight-Resistant IR Receiver

A high-performance design might combine:

Laboratory tests show such systems achieve BER < 10−6 under direct sunlight (100 klux).

Practical Considerations

In industrial settings, flickering from high-intensity discharge (HID) lamps requires additional notch filtering at harmonics of the mains frequency (50/60 Hz and multiples).

IR Signal vs. Ambient Noise Spectra with Modulation A dual-axis plot showing spectral power densities (signal, noise, and filter response) and time-domain signals (raw vs. modulated) for infrared communication systems. Wavelength (λ) Power Density N(λ) S(λ) T(λ) λ₁ λ₂ Time Amplitude Raw Signal 38 kHz Carrier
Diagram Description: The section involves spectral relationships (signal vs. noise power densities) and modulation techniques that are best visualized with overlapping spectra and time-domain waveforms.

5.3 Power Consumption and Efficiency

Power Dissipation in IR Transmitters

The dominant source of power consumption in infrared (IR) communication systems is the transmitter, primarily due to the forward current required to drive the IR LED. The instantaneous power dissipation Pdiss in an IR LED is given by:

$$ P_{diss} = V_f \cdot I_f $$

where Vf is the forward voltage drop (typically 1.2–1.6 V for GaAs LEDs) and If is the forward current. For pulsed operation, the average power Pavg must account for the duty cycle D:

$$ P_{avg} = D \cdot V_f \cdot I_f $$

High-speed communication often demands short, high-current pulses (e.g., 50–100 mA) with low duty cycles (1–10%), reducing average power but requiring careful thermal management.

Modulation Efficiency

Efficiency in IR systems is heavily influenced by the modulation scheme. On-off keying (OOK), the most common method, has a theoretical power efficiency ηmod of:

$$ \eta_{mod} = \frac{P_{\text{peak}} \cdot D}{P_{\text{avg}}} $$

where Ppeak is the peak optical power. For example, a 38 kHz carrier modulated at 50% duty cycle with a 100 mA pulse achieves ~40% efficiency, while subcarrier modulation (e.g., PWM or PPM) can improve this to 60–70% by optimizing pulse positioning.

Receiver Sensitivity and Power Trade-offs

The minimum detectable power Pmin at the receiver is governed by the photodiode's responsivity R (A/W) and noise equivalent power (NEP):

$$ P_{min} = \frac{\sqrt{2q I_d \Delta f}}{R} $$

where Id is the dark current and Δf is the bandwidth. To minimize transmitter power, receivers often employ transimpedance amplifiers (TIAs) with high gain (>1 MΩ) and low input-referred noise (<1 pA/√Hz).

Thermal Constraints

Junction temperature rise in IR LEDs follows:

$$ \Delta T_j = R_{th} \cdot P_{diss} $$

where Rth is the thermal resistance (typically 50–200 °C/W for SMD LEDs). Exceeding the maximum junction temperature (often 85–125°C) degrades output power and lifetime. Heat sinks or pulsed operation mitigate this.

Case Study: Remote Control Optimization

In TV remotes, a 940 nm LED driven at 50 mA (1.4 V) with 5% duty cycle consumes:

$$ P_{avg} = 0.05 \times 1.4 \times 0.05 = 3.5 \text{ mW} $$

Modern designs achieve < 1 mW average power by using adaptive pulse-width modulation and sleep modes between transmissions.

6. Key Research Papers and Articles

6.1 Key Research Papers and Articles

6.2 Recommended Books on IR Communication

6.3 Online Resources and Tutorials