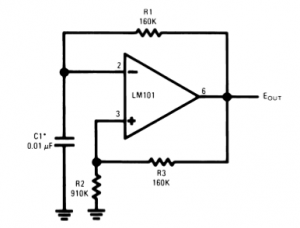
Integrators and Differentiators

1. Definition and Mathematical Basis

Integrators and Differentiators: Definition and Mathematical Basis

Fundamental Concepts

Integrators and differentiators are fundamental analog circuits that perform mathematical operations on input signals. An integrator computes the time integral of an input voltage, while a differentiator computes its time derivative. These circuits are implemented using operational amplifiers (op-amps) with capacitive feedback or input elements, exploiting the current-voltage relationship in capacitors.

Mathematical Formulation of an Integrator

The output voltage \( V_{out}(t) \) of an ideal integrator relates to its input voltage \( V_{in}(t) \) by:

$$ V_{out}(t) = -\frac{1}{RC} \int_{0}^{t} V_{in}(\tau) \, d\tau + V_{initial} $$

where:

This equation derives from the capacitor's current-voltage relationship \( I_C = C \frac{dV}{dt} \) and the op-amp's virtual ground principle. For a sinusoidal input \( V_{in}(t) = V_0 \sin(\omega t) \), the output becomes:

$$ V_{out}(t) = \frac{V_0}{\omega RC} \cos(\omega t) $$

Mathematical Formulation of a Differentiator

An ideal differentiator produces an output proportional to the derivative of the input:

$$ V_{out}(t) = -RC \frac{dV_{in}(t)}{dt} $$

Here, the capacitor is placed at the input, and the resistor serves as the feedback element. For a sinusoidal input, the output becomes:

$$ V_{out}(t) = -\omega RC V_0 \cos(\omega t) $$

Frequency Domain Analysis

In the Laplace domain, the integrator and differentiator transfer functions are:

$$ H_{int}(s) = -\frac{1}{RCs} \quad \text{(Integrator)} $$ $$ H_{diff}(s) = -RCs \quad \text{(Differentiator)} $$

These reveal that integrators act as low-pass filters (magnitude \( \propto 1/\omega \)), while differentiators act as high-pass filters (magnitude \( \propto \omega \)).

Practical Limitations

Real-world integrators suffer from:

Differentiators face:

These limitations are mitigated by adding parallel resistors (for integrators) or series resistors (for differentiators) to constrain gain at extreme frequencies.

Op-Amp Integrator and Differentiator Circuits Side-by-side comparison of op-amp integrator (left) and differentiator (right) circuits, showing component placements and signal flow. R C V_in V_out Integrator C R V_in V_out Differentiator
Diagram Description: The diagram would show the op-amp circuit configurations for integrators and differentiators, including component placements and signal flow.

1.2 Role in Signal Processing

Fundamental Operations in Analog Signal Processing

Integrators and differentiators are foundational building blocks in analog signal processing, enabling mathematical operations on continuous-time signals. An integrator computes the time integral of an input signal, while a differentiator calculates its time derivative. These operations are implemented using operational amplifiers (op-amps) with capacitive feedback or input elements, shaping the frequency response of the circuit.

$$ V_{\text{out}}(t) = -\frac{1}{RC} \int_{0}^{t} V_{\text{in}}(\tau) \, d\tau \quad \text{(Integrator)} $$
$$ V_{\text{out}}(t) = -RC \frac{dV_{\text{in}}(t)}{dt} \quad \text{(Differentiator)} $$

Frequency Domain Analysis

In the frequency domain, an integrator exhibits a transfer function proportional to \( \frac{1}{j\omega} \), introducing a phase shift of \(-90^\circ\) and a roll-off of \(-20\,\text{dB/decade}\). A differentiator, conversely, has a transfer function proportional to \( j\omega \), providing a \(+90^\circ\) phase shift and a \(+20\,\text{dB/decade}\) gain slope. These characteristics make them essential for shaping signal spectra in filters, control systems, and modulation/demodulation circuits.

Practical Applications

Waveform Generation and Shaping

Integrators convert square waves into triangular waves and are used in function generators. Differentiators extract edges from pulse waveforms, aiding in edge detection for clock recovery circuits.

Control Systems

In PID controllers, integrators eliminate steady-state error by accumulating past errors, while differentiators provide damping by anticipating future error trends. The combination improves system stability and response time.

Analog Computing

Integrators solve differential equations in analog computers, simulating physical systems like mechanical oscillators or thermal dynamics. Differentiators model rate-dependent phenomena, such as velocity or acceleration in motion systems.

Limitations and Compensation

Practical integrators suffer from DC drift due to op-amp input bias currents, often mitigated with a large parallel resistor. Differentiators are prone to high-frequency noise amplification, necessitating a series resistor to limit bandwidth. These trade-offs are critical in precision applications like medical instrumentation or aerospace systems.

Modern Implementations

While discrete op-amp circuits remain prevalent, switched-capacitor integrators in ICs offer precise time-constant control via clock frequencies, enabling adaptive filters in communication systems like software-defined radios.

Integrator/Differentiator Waveform Transformations and Frequency Responses Dual-axis diagram showing time-domain waveforms (square to triangular for integrator, pulse to spikes for differentiator) and frequency-domain Bode plots (magnitude and phase) for both circuits. Time Domain Waveforms Integrator t Vin(t) Vout(t) Differentiator t Vin(t) Vout(t) Frequency Response (Bode Plots) Integrator f |H| -20dB/decade ∠H -90° Differentiator f |H| +20dB/decade ∠H +90° Input Output
Diagram Description: The section describes waveform transformations (square to triangular waves) and frequency domain behaviors (phase shifts, roll-off slopes), which are inherently visual concepts.

1.3 Key Differences Between Integrators and Differentiators

Fundamental Operational Principles

Integrators and differentiators are both op-amp-based circuits, but their mathematical operations and frequency responses are fundamentally opposed. An integrator computes the time integral of the input signal, while a differentiator calculates its time derivative. The transfer functions reveal this distinction clearly:

$$ H_{\text{int}}(s) = -\frac{1}{RCs} \quad \text{(Integrator)} $$
$$ H_{\text{diff}}(s) = -RCs \quad \text{(Differentiator)} $$

Here, the integrator's transfer function has a pole at the origin ($$s = 0$$), making it inherently low-pass, while the differentiator's zero at the origin ($$s = 0$$) gives it a high-pass characteristic.

Frequency Response and Stability

Integrators exhibit a roll-off of -20 dB/decade in their magnitude response, making them ideal for applications like low-pass filtering or waveform generation (e.g., triangular waves from square waves). Differentiators, conversely, have a +20 dB/decade gain slope, amplifying high-frequency noise—a critical limitation in practical implementations.

Stability concerns differ as well. Integrators are prone to DC drift due to the capacitive feedback path, often requiring a parallel resistor to limit low-frequency gain. Differentiators, however, risk instability from high-frequency noise amplification, necessitating a series resistor to mitigate phase margin degradation.

Circuit Topology and Component Roles

The core difference lies in the placement of reactive components:

Practical Applications and Limitations

Integrators are widely used in:

Differentiators find niche use in:

However, differentiators are less common due to their noise sensitivity. Modern systems often replace them with digital signal processing (DSP) or active filter designs.

Mathematical Derivation of Time-Domain Responses

For an integrator with input voltage $$V_{\text{in}}(t)$$, the output is:

$$ V_{\text{out}}(t) = -\frac{1}{RC} \int_0^t V_{\text{in}}(\tau) \, d\tau + V_{\text{out}}(0) $$

where $$V_{\text{out}}(0)$$ is the initial condition. For a differentiator:

$$ V_{\text{out}}(t) = -RC \frac{dV_{\text{in}}(t)}{dt} $$

These equations highlight the inverse relationship between the two operations.

Noise and Component Selection

Component choice critically impacts performance. Integrators require:

Differentiators demand:

Integrator vs. Differentiator Circuit Topologies Side-by-side schematic comparison of integrator (left) and differentiator (right) circuits, showing opposing component placements (feedback capacitor vs. input capacitor) and signal flow. + - R_in C_f V_in V_out + - C_in R_f V_in V_out Integrator Differentiator
Diagram Description: A side-by-side schematic comparison of integrator and differentiator circuits would visually clarify the opposing component placements (feedback capacitor vs. input capacitor) and signal flow.

2. Op-Amp Integrator: Circuit Design and Analysis

2.1 Op-Amp Integrator: Circuit Design and Analysis

Basic Configuration and Ideal Behavior

The operational amplifier (op-amp) integrator performs the mathematical operation of integration on an input signal. The fundamental configuration consists of an op-amp with a capacitor in the feedback loop and a resistor at the input. The ideal transfer function of the integrator is derived from the virtual ground principle and the current balance at the inverting input.

$$ V_{out}(t) = -\frac{1}{RC} \int V_{in}(t) \, dt $$

Where R is the input resistance, C is the feedback capacitance, and Vin(t) is the time-dependent input voltage. The negative sign indicates phase inversion due to the inverting configuration.

Derivation of the Transfer Function

Applying Kirchhoff’s current law (KCL) at the inverting input node (V−) and assuming an ideal op-amp (infinite gain, infinite input impedance, and zero output impedance), the current through the resistor R equals the current through the capacitor C:

$$ \frac{V_{in} - V_{-}}{R} = C \frac{d(V_{-} - V_{out})}{dt} $$

Since V− ≈ V+ = 0 (virtual ground), this simplifies to:

$$ \frac{V_{in}}{R} = -C \frac{dV_{out}}{dt} $$

Rearranging and integrating both sides yields the output voltage:

$$ V_{out}(t) = -\frac{1}{RC} \int V_{in}(t) \, dt + V_{out}(0) $$

where Vout(0) represents the initial condition of the capacitor voltage.

Practical Limitations and DC Offset

In real-world applications, the ideal integrator suffers from DC drift due to input bias currents and offset voltages. Even a small DC component in Vin causes the capacitor to charge continuously, eventually saturating the op-amp. To mitigate this, a large resistor Rf is placed in parallel with C to provide DC feedback, forming a lossy integrator:

$$ V_{out}(t) = -\frac{1}{R_fC} \int V_{in}(t) \, dt - \frac{R_f}{R} V_{in}(t) $$

The second term introduces a proportional response, limiting the integrator’s low-frequency gain.

Frequency Response and Stability

The frequency-domain transfer function of an ideal integrator is:

$$ H(j\omega) = -\frac{1}{j\omega RC} $$

This implies a constant phase shift of −90° and a gain that decreases at 20 dB/decade. However, practical op-amps have finite gain-bandwidth product (GBW) and slew rate limitations, which introduce deviations from ideal behavior at high frequencies. Stability can be improved by adding a small resistor in series with the feedback capacitor to reduce phase margin degradation.

Design Considerations

Applications

Op-amp integrators are widely used in:

R C Op-Amp
Op-Amp Integrator Circuit A schematic diagram of an operational amplifier configured as an integrator circuit with resistor (R) at the input and capacitor (C) in the feedback loop. + - Op-Amp R C Vin Vout
Diagram Description: The diagram would physically show the op-amp integrator circuit configuration with the resistor (R) at the input and the capacitor (C) in the feedback loop, including the op-amp symbol and connections.

2.2 Practical Limitations of Op-Amp Integrators

Finite Gain-Bandwidth Product

The ideal integrator assumes an op-amp with infinite gain and bandwidth. However, real op-amps have a finite gain-bandwidth product (GBWP), which introduces errors in the integration. The transfer function of a practical integrator must account for the op-amp's open-loop gain AOL and its frequency dependence:

$$ A_{OL}(f) = \frac{A_0}{1 + j\frac{f}{f_c}} $$

where A0 is the DC gain and fc is the cutoff frequency. The finite GBWP causes the integrator to deviate from ideal behavior at higher frequencies, introducing phase errors and gain roll-off.

Input Offset Voltage and Bias Currents

Non-ideal op-amp characteristics, such as input offset voltage (VOS) and input bias currents (IB), lead to output drift in integrators. The offset voltage causes the capacitor to charge or discharge slowly, even with no input signal, resulting in a ramping output:

$$ V_{out}(t) = -\frac{V_{OS}}{RC} t $$

Similarly, input bias currents generate an offset current that charges the capacitor, further contributing to output drift. Precision integrators require low-offset op-amps and compensation techniques such as resistor matching or auto-zeroing circuits.

Capacitor Leakage and Dielectric Absorption

Real capacitors exhibit leakage currents and dielectric absorption, which distort the integration process. Leakage current (Ileak) introduces an error term:

$$ V_{out}(t) = -\frac{1}{C} \int_0^t (I_{in} + I_{leak}) \, dt $$

Dielectric absorption causes voltage recovery after discharge, leading to hysteresis effects. Polypropylene or polystyrene capacitors are preferred for high-precision integrators due to their low leakage and dielectric absorption.

Saturation and Dynamic Range

Integrators accumulate charge over time, which can drive the output into saturation if not reset periodically. The output voltage range is limited by the op-amp's supply rails (VCC and VEE). For a sinusoidal input Vin = Vp sin(ωt), the output amplitude grows as:

$$ V_{out} = \frac{V_p}{ωRC} $$

At low frequencies, the output can saturate quickly, necessitating a reset mechanism (e.g., a parallel reset switch or a feedback resistor to limit DC gain).

Noise and Stability Considerations

Integrators amplify low-frequency noise due to their high gain at DC. The noise gain of an integrator is:

$$ NG(f) = \left| 1 + \frac{Z_f}{Z_{in}} \right| = \left| 1 + \frac{1}{jωRC} \right| $$

This amplifies 1/f noise and DC drift. Stability is also a concern, as the integrator's phase shift approaches -180° at high frequencies, risking oscillation. A feedback resistor (Rf) is often added to stabilize the circuit by introducing a zero in the transfer function.

Practical Compensation Techniques

Practical Op-Amp Integrator Limitations and Compensation A combined schematic and waveform diagram showing an op-amp integrator circuit with practical limitations like output drift, saturation, and noise gain, along with compensation techniques. Op-Amp R C V_out R_f Reset Non-Ideal Effects: V_OS: Input offset voltage I_B: Input bias current V_out(t) drift V_CC V_EE NG(f) Time Amplitude Practical Op-Amp Integrator Limitations and Compensation
Diagram Description: The section discusses practical limitations like output drift, saturation, and noise amplification, which would benefit from visual representation of waveforms and circuit modifications.

2.3 Op-Amp Differentiator: Circuit Design and Analysis

The operational amplifier (op-amp) differentiator is a fundamental analog circuit that performs mathematical differentiation on an input signal. Its output voltage is proportional to the rate of change of the input voltage with respect to time. This section rigorously examines the circuit's design, mathematical derivation, stability considerations, and practical limitations.

Basic Differentiator Circuit

The ideal op-amp differentiator consists of a capacitor in the input path and a resistor in the feedback loop. The input signal Vin(t) is applied through capacitor C, while resistor R connects the output to the inverting input. The non-inverting input is grounded to maintain a virtual ground at the inverting terminal.

$$ V_{out}(t) = -RC \frac{dV_{in}(t)}{dt} $$

This equation holds under ideal conditions, where the op-amp has infinite gain, infinite bandwidth, and zero input bias current. The negative sign indicates signal inversion, characteristic of inverting configurations.

Derivation of the Transfer Function

Applying Kirchhoff's current law at the inverting input node (virtual ground) yields:

$$ C \frac{dV_{in}}{dt} = -\frac{V_{out}}{R} $$

Rearranging this gives the fundamental differentiator equation. In the frequency domain, the impedance of the capacitor ZC = 1/(jωC) leads to the transfer function:

$$ H(j\omega) = \frac{V_{out}}{V_{in}} = -j\omega RC $$

This shows the output magnitude increases linearly with frequency (20 dB/decade slope), making the circuit inherently susceptible to high-frequency noise.

Stability and Practical Modifications

The ideal differentiator's open-loop gain rolls off at -20 dB/decade, while the feedback network's +20 dB/decade creates a 40 dB/decade net slope that can cause oscillation. Two critical modifications address this:

The modified transfer function becomes:

$$ H(j\omega) = -\frac{j\omega RC}{1 + j\omega R_1C} \cdot \frac{1}{1 + j\omega RC_f} $$

Component Selection Guidelines

Practical differentiator design requires careful component selection:

Real-World Limitations

Non-ideal characteristics impose additional constraints:

Applications in Signal Processing

Differentiators find use in several advanced applications:

Stability and Noise Considerations in Differentiators

High-Frequency Instability in Ideal Differentiators

An ideal differentiator has a transfer function given by:

$$ H(s) = sRC $$

where s is the complex frequency variable. This implies a gain that increases linearly with frequency (|H(jω)| = ωRC), making the circuit inherently unstable at high frequencies. In practice, this results in excessive amplification of high-frequency noise and potential oscillation due to parasitic capacitances and inductances.

Noise Amplification and Bandwidth Limitations

Differentiators amplify high-frequency noise because their gain rises with ω. For a white noise input with spectral density Sn(f), the output noise power is:

$$ V_{n,\text{out}}^2 = \int_0^\infty |H(j2\pi f)|^2 S_n(f) \, df = (RC)^2 \int_0^\infty (2\pi f)^2 S_n(f) \, df $$

This integral diverges for ideal white noise, necessitating bandwidth-limiting modifications. A practical differentiator introduces a pole to roll off the gain at high frequencies:

$$ H(s) = \frac{sRC}{1 + sR_fC} $$

where Rf is a feedback resistor that stabilizes the circuit.

Stabilization Techniques

To mitigate instability, engineers employ:

Practical Design Example

A stabilized differentiator for a 10 kHz bandwidth might use:

$$ R = 1\,\text{k}\Omega,\; C = 10\,\text{nF},\; R_f = 100\,\Omega $$

yielding a transfer function with a pole at fp = 1/(2πRfC) ≈ 160\,\text{kHz}. The phase margin is improved by ensuring the operational amplifier’s unity-gain frequency is well above fp.

Noise Reduction Strategies

Key methods to minimize noise include:

Case Study: Differentiator in PID Control

In proportional-integral-derivative (PID) controllers, differentiators process error signals. Instability arises if the derivative gain (Kd) is too high, exciting high-frequency modes. A common fix is to replace the ideal differentiator with a lead-lag network:

$$ H(s) = \frac{K_d s}{1 + s\tau} $$

where τ is chosen to attenuate frequencies beyond the system’s mechanical or electrical resonances.

Stabilized Differentiator Circuit and Frequency Response A schematic of a stabilized differentiator circuit with an op-amp, resistor (R), capacitor (C), feedback resistor (Rf), and its corresponding Bode plot showing magnitude (dB) versus frequency (log scale). Vout Vin C R Rf H(s) = sRC / (1 + sRfC) Frequency (log scale) Magnitude (dB) +20dB/dec fp Roll-off
Diagram Description: The section discusses transfer functions and stabilization techniques that would benefit from a visual representation of the modified differentiator circuit and its frequency response.

3. Waveform Generation and Shaping

Waveform Generation and Shaping

Integrators and differentiators are fundamental building blocks in analog signal processing, enabling precise waveform manipulation. Their behavior is derived from the time-domain response of RC and op-amp circuits, governed by the interaction between capacitive reactance and resistive elements.

Time-Domain Analysis of Integrators

An ideal integrator produces an output voltage proportional to the time integral of the input signal. For an op-amp-based integrator with feedback capacitor C and input resistor R, the transfer function in the Laplace domain is:

$$ H(s) = -\frac{1}{RCs} $$

Converting to the time domain, the output voltage Vout(t) becomes:

$$ V_{out}(t) = -\frac{1}{RC} \int_0^t V_{in}(\tau) \, d\tau + V_{initial} $$

where Vinitial accounts for initial capacitor charge. Practical integrators include a parallel feedback resistor to prevent DC drift, modifying the transfer function to:

$$ H(s) = -\frac{R_f}{R} \cdot \frac{1}{1 + R_fCs} $$

Differentiator Circuit Dynamics

A differentiator generates an output proportional to the input signal's time derivative. The ideal transfer function is:

$$ H(s) = -RCs $$

In practice, high-frequency noise amplification necessitates a series input resistor R1, yielding:

$$ H(s) = -\frac{RCs}{1 + R_1Cs} $$

This creates a band-limited differentiator with a pole at f = 1/(2πR1C).

Waveform Transformation Examples

These circuits enable key waveform transformations:

Stability Considerations

Practical implementations must address:

Advanced Applications

Modern implementations leverage these principles in:

Input Square Wave Integrated Triangular Wave
Integrator/Differentiator Waveform Transformations Diagram showing the transformation of a square wave input to a triangular wave output through an RC integrator circuit with an op-amp. Vin (Square Wave) 0 T/2 T 3T/2 2T RC Integrator Op-Amp R C Vout (Triangular Wave) 0 T/2 T 3T/2 2T
Diagram Description: The section demonstrates waveform transformations (square-to-triangle conversion) and circuit dynamics that are inherently visual.

3.2 Frequency Domain Applications (Filters, PLLs)

Integrators and Differentiators as Frequency-Selective Filters

In the frequency domain, integrators and differentiators exhibit distinct filtering characteristics due to their transfer functions. An ideal integrator has a transfer function:

$$ H(\omega) = \frac{1}{j\omega RC} $$

This corresponds to a first-order low-pass filter with a -20 dB/decade roll-off. The magnitude response is:

$$ |H(\omega)| = \frac{1}{\omega RC} $$

Conversely, an ideal differentiator has the transfer function:

$$ H(\omega) = j\omega RC $$

This implements a first-order high-pass filter with a +20 dB/decade gain slope. The magnitude response is:

$$ |H(\omega)| = \omega RC $$

Practical implementations must account for finite op-amp bandwidth, which introduces additional poles and modifies the ideal response. For stability, a feedback resistor is often added to the integrator, limiting its DC gain.

Phase-Locked Loops (PLLs) and Frequency Synthesis

Integrators play a critical role in PLLs, particularly in the loop filter stage. A second-order PLL with a charge-pump phase detector and passive loop filter has a transfer function:

$$ G(s) = \frac{K_{\phi}K_{VCO}}{N} \cdot \frac{1 + s\tau_2}{s^2\tau_1} $$

where:

The integrator (1/s term) ensures infinite DC gain, enabling zero steady-state phase error. Differentiators (via the sτ2 zero) improve transient response and stability.

Applications in Frequency Synthesis

PLL-based frequency synthesizers leverage these principles to generate stable, programmable output frequencies. Key metrics include:

Modern fractional-N synthesizers use sigma-delta modulation to achieve fine frequency resolution while avoiding integer-N spurs.

Active Filter Design Techniques

Integrators form the basis of higher-order active filters. A Sallen-Key low-pass filter, for example, can be analyzed as a cascade of integrators with feedback:

$$ H(s) = \frac{K\omega_0^2}{s^2 + \frac{\omega_0}{Q}s + \omega_0^2} $$

where Q is the quality factor and ω0 is the cutoff frequency. The Q factor is set by the ratio of integrator gains:

$$ Q = \frac{1}{2}\sqrt{\frac{R_1C_1}{R_2C_2}} $$

State-variable filters explicitly use integrators to implement simultaneous low-pass, band-pass, and high-pass outputs with orthogonal tuning.

Integrator/Differentiator Frequency Responses & PLL Block Diagram Dual-panel diagram showing Bode plots of integrator and differentiator frequency responses (left) and a PLL block diagram with signal flow (right). Frequency Response Magnitude (dB) 0 20 -20 Frequency (rad/s) Integrator Differentiator Phase (deg) Frequency (rad/s) -90° +90° PLL Block Diagram Phase Detector Kφ Loop Filter F(s) VCO KVCO/s Divider 1/N Feedback Path
Diagram Description: The section discusses frequency response characteristics and PLL block relationships that are inherently visual.

Integrators and Differentiators in Control Systems and Feedback Loops

Role in Control System Dynamics

Integrators and differentiators serve as fundamental building blocks in control systems, shaping the dynamic response of feedback loops. An integrator, with its transfer function $$H(s) = \frac{1}{s\tau_i}$$, introduces a pole at the origin, ensuring zero steady-state error for step inputs by accumulating past errors. Conversely, a differentiator ($$H(s) = s\tau_d$$) anticipates future error trends, improving transient response but amplifying high-frequency noise.

Mathematical Representation in PID Control

The proportional-integral-derivative (PID) controller leverages both functions:

$$ u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{de(t)}{dt} $$

where Ki and Kd govern the integrator and differentiator contributions. The Bode plot of a PID controller reveals:

Stability Considerations

Integrators can induce phase lag (90° per pole), risking instability in high-gain systems. The Nyquist stability criterion quantifies this through the gain margin Gm and phase margin ϕm. For a system with open-loop transfer function $$L(s) = \frac{K}{s(s+a)}$$, the phase margin is:

$$ \phi_m = 180° + \angle L(j\omega_c) $$

where ωc is the crossover frequency. Excessive derivative gain can destabilize systems by introducing high-frequency noise amplification.

Practical Implementation Challenges

Real-world constraints necessitate modifications:

Case Study: Motor Position Control

A DC motor’s angular position θ(t) requires double integration of the input voltage V(t):

$$ \theta(t) = \int \left( \int \frac{K_t V(t) - B\dot{\theta}(t)}{J} dt \right) dt $$

where Kt, B, and J are torque constant, damping, and inertia. A PID controller compensates for the plant’s inherent double integrator, with:

|H(s)| ∠H(s)
PID Controller Bode Plot and Motor Control System A combined diagram showing a Bode plot (magnitude and phase) and a block diagram of a PID-controlled motor system. Magnitude (dB) Phase (°) 10⁰ 10¹ 10² 10³ ω (rad/s) ω_c G_m φ_m PID K_p, K_i, K_d Motor θ(t), V(t) 1/s² ω_n
Diagram Description: The section discusses Bode plots, PID control dynamics, and motor position control, which are highly visual concepts involving frequency response and system behavior.

4. Recommended Textbooks and Papers

4.1 Recommended Textbooks and Papers

4.2 Online Resources and Tutorials

4.3 Advanced Topics for Further Study