Low Pass Filters

1. Definition and Purpose of Low Pass Filters

Definition and Purpose of Low Pass Filters

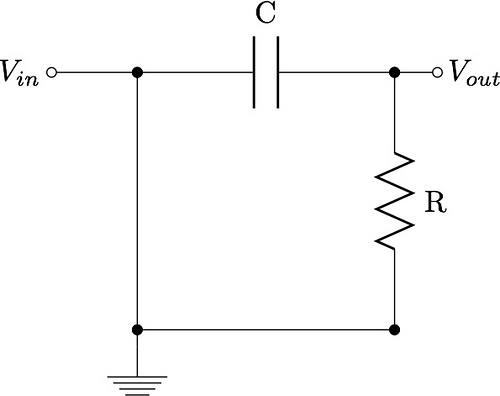
A low pass filter (LPF) is an electronic circuit designed to attenuate signals with frequencies above a specified cutoff frequency ($$f_c$$) while allowing signals below this frequency to pass with minimal attenuation. The fundamental purpose of an LPF is to eliminate high-frequency noise, prevent aliasing in analog-to-digital conversion, and shape signal bandwidth in communication systems.

Mathematical Foundation

The frequency response of an ideal LPF is characterized by a brick-wall transition at $$f_c$$, but real-world filters exhibit a gradual roll-off. The transfer function $$H(f)$$ of a first-order passive RC LPF is derived from Kirchhoff’s laws:

$$ H(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j2\pi fRC} $$

where $$R$$ is resistance, $$C$$ is capacitance, and $$j$$ is the imaginary unit. The magnitude response in decibels (dB) is:

$$ |H(f)|_{dB} = 20 \log_{10} \left( \frac{1}{\sqrt{1 + (f/f_c)^2}} \right) $$

The cutoff frequency $$f_c$$ is defined as the point where the power drops to half (-3 dB) of the passband value:

$$ f_c = \frac{1}{2\pi RC} $$

Practical Applications

Real-World Tradeoffs

Practical LPFs deviate from ideal behavior due to:

Design Considerations

Selecting an LPF topology depends on:

Low Pass Filter Frequency Response Frequency response curve of a low pass filter showing the cutoff frequency, passband, stopband, and roll-off slope. 10 100 1k 10k 100k -20 -40 -60 Frequency (Hz) Magnitude (dB) f_c -3 dB Passband Stopband -20 dB/decade
Diagram Description: The diagram would show the frequency response curve of a low pass filter, illustrating the cutoff frequency, passband, and roll-off region.

Frequency Response Characteristics

The frequency response of a low-pass filter (LPF) defines how the filter attenuates or passes signals as a function of frequency. For an ideal LPF, the gain is unity (0 dB) in the passband and zero in the stopband, with an instantaneous transition at the cutoff frequency. However, real filters exhibit gradual roll-off and non-ideal behavior, which can be rigorously analyzed using transfer functions and Bode plots.

Transfer Function of a First-Order RC Low-Pass Filter

The simplest LPF is the first-order RC filter, characterized by a single pole in its transfer function. The voltage across the capacitor (Vout) relative to the input voltage (Vin) is given by:

$$ H(j\omega) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j\omega RC} $$

where R is the resistance, C the capacitance, and ω the angular frequency (ω = 2πf). The magnitude and phase response are derived as:

$$ |H(j\omega)| = \frac{1}{\sqrt{1 + (\omega RC)^2}} $$
$$ \phi(\omega) = -\tan^{-1}(\omega RC) $$

The cutoff frequency (fc), where the output power is halved (−3 dB point), occurs when ωRC = 1:

$$ f_c = \frac{1}{2\pi RC} $$

Second-Order and Higher-Order Filter Responses

Higher-order filters provide steeper roll-off rates, critical for applications requiring sharp transition bands. A second-order LPF, such as a Butterworth filter, has a transfer function:

$$ H(j\omega) = \frac{1}{1 + j\omega \frac{RC}{Q} + (j\omega RC)^2} $$

where Q (quality factor) determines the damping and peaking near the cutoff frequency. For a Butterworth filter (maximally flat passband), Q = 0.707, yielding a roll-off of −40 dB/decade.

Key Frequency Response Metrics

Bode Plot Analysis

A Bode plot visualizes the magnitude (in dB) and phase (in degrees) responses. For a first-order LPF:

For a second-order Butterworth filter, the phase shift extends to −180°, and the magnitude roll-off doubles to −40 dB/decade.

Practical Implications

In RF and audio systems, LPFs suppress high-frequency noise and harmonics. For example, a 5th-order LPF in a DAC reconstruction filter ensures negligible aliasing artifacts. The choice of filter type (Butterworth, Chebyshev, Bessel) trades off roll-off steepness, phase linearity, and passband ripple.

fc -3 dB
Bode Plot for 1st and 2nd Order LPFs A Bode plot showing magnitude (dB) and phase (degrees) vs. frequency for 1st and 2nd order low-pass filters, with labeled cutoff frequencies and roll-off slopes. Magnitude (dB) dB Frequency (log scale) 0 -20 -40 -60 -80 f_c/10 f_c 10f_c 100f_c f_c -20 dB/dec -3 dB -40 dB/dec Phase (degrees) Degrees Frequency (log scale) 0° -45° -90° -135° -180° f_c/10 f_c 10f_c 100f_c -90° -180° Legend 1st Order 2nd Order
Diagram Description: The section describes Bode plots and frequency response curves, which are inherently visual concepts showing magnitude/phase vs. frequency.

Cutoff Frequency and Roll-off

Definition of Cutoff Frequency

The cutoff frequency (fc) of a low-pass filter is the frequency at which the output signal power is reduced to half (-3 dB) of its maximum passband value. This corresponds to the point where the voltage gain drops to

$$ \frac{1}{\sqrt{2}} \approx 0.707 $$
of its peak value. For a first-order RC low-pass filter, the cutoff frequency is derived from the time constant τ = RC:

$$ f_c = \frac{1}{2\pi RC} $$

Derivation of the -3 dB Point

The -3 dB reference arises from the logarithmic decibel scale, where power ratio is expressed as:

$$ 10 \log_{10}\left(\frac{P_{\text{out}}}{P_{\text{in}}}\right) $$

At fc, the output power is halved, leading to:

$$ 10 \log_{10}\left(\frac{1}{2}\right) \approx -3 \text{ dB} $$

Roll-off Rate

The roll-off rate describes how rapidly the filter attenuates signals beyond fc. For an n-th order filter, the roll-off is:

$$ 20n \text{ dB/decade} \quad \text{or} \quad 6n \text{ dB/octave} $$

For example, a first-order filter (n = 1) attenuates at 20 dB/decade, while a second-order Butterworth filter achieves 40 dB/decade.

Phase Response and Group Delay

Near fc, the phase shift introduced by a first-order filter is -45°. The group delay, defined as the negative derivative of phase with respect to angular frequency (τ_g = -d\phi/dω), is critical for preserving signal integrity in time-domain applications. For an RC filter:

$$ \tau_g = RC \quad \text{(constant in the passband)} $$

Practical Implications

Higher-Order Filters and Roll-off Enhancement

Butterworth, Chebyshev, and Bessel filters trade off roll-off steepness for passband ripple or phase linearity. For instance, an 8th-order Chebyshev filter can achieve >100 dB/decade roll-off but introduces passband ripple:

$$ |H(j\omega)| = \frac{1}{\sqrt{1 + \epsilon^2 T_n^2(\omega/\omega_c)}} $$

where Tn is the Chebyshev polynomial of order n, and ϵ controls ripple magnitude.

Low-Pass Filter Frequency Response A Bode plot showing the magnitude (dB) and phase angle response of a low-pass filter with labeled cutoff frequency, roll-off rate, and phase shift. 0 -20 -40 -60 Magnitude (dB) 10 100 1k 10k Frequency (Hz) 0° -45° -90° Phase (°) -3 dB 20 dB/decade Passband Stopband -45° fc
Diagram Description: The section covers frequency response, roll-off rates, and phase shifts, which are best visualized with a Bode plot or frequency response graph.

2. Passive Low Pass Filters

2.1 Passive Low Pass Filters

Passive low pass filters (LPFs) are fundamental building blocks in signal processing, constructed using only passive components—resistors, capacitors, and inductors—without amplification. Their operation relies on frequency-dependent impedance to attenuate high-frequency signals while allowing low-frequency components to pass.

First-Order RC Low Pass Filter

The simplest passive LPF is the first-order RC filter, consisting of a resistor R and capacitor C in series. The transfer function H(f) describes the output-to-input voltage ratio as a function of frequency:

$$ H(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j2\pi fRC} $$

The magnitude response, calculated as |H(f)|, reveals the filter's attenuation characteristics:

$$ |H(f)| = \frac{1}{\sqrt{1 + (2\pi fRC)^2}} $$

The cutoff frequency fc, where the output power drops to half (-3 dB) of the input, is derived by setting |H(f)| = 1/√2:

$$ f_c = \frac{1}{2\pi RC} $$

First-Order RL Low Pass Filter

An alternative implementation replaces the capacitor with an inductor L. The transfer function and cutoff frequency for this RL configuration are:

$$ H(f) = \frac{R}{R + j2\pi fL} $$ $$ f_c = \frac{R}{2\pi L} $$

While RL filters are less common due to inductor non-idealities (e.g., parasitic resistance and size), they remain relevant in high-current applications where capacitors are impractical.

Second-Order Passive LC Filters

Higher-order filters improve roll-off steepness. A second-order LPF combines L and C to form an LC tank circuit. The transfer function for this RLC configuration is:

$$ H(f) = \frac{1}{1 - (2\pi f)^2LC + j2\pi fRC} $$

The cutoff frequency and quality factor Q are critical design parameters:

$$ f_c = \frac{1}{2\pi \sqrt{LC}} $$ $$ Q = \frac{1}{R} \sqrt{\frac{L}{C}} $$

A high Q (>0.707) introduces peaking near fc, while Q = 0.707 yields a Butterworth response with maximally flat passband.

Practical Considerations

Applications

Passive LPFs are ubiquitous in:

R C Vin Vout
Passive LPF Circuit Comparison Side-by-side comparison of RC, RL, and LC passive low-pass filter circuits with component labels and cutoff frequency formulas. V_in R C V_out f_c = 1/(2πRC) RC Filter V_in R L V_out f_c = R/(2πL) RL Filter V_in L C V_out f_c = 1/(2π√(LC)) LC Filter Passive Low-Pass Filter Circuits
Diagram Description: The section explains RC, RL, and LC filter circuits with transfer functions, which are inherently visual concepts requiring component arrangement and signal flow visualization.

2.2 Active Low Pass Filters

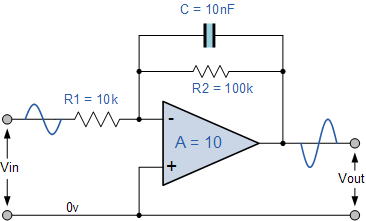
Active low pass filters incorporate operational amplifiers (op-amps) to provide gain and improve performance compared to passive RC filters. The op-amp's high input impedance prevents loading effects, while its low output impedance ensures signal integrity when driving subsequent stages. These filters are widely used in audio processing, anti-aliasing in ADCs, and noise reduction in communication systems.

First-Order Active Low Pass Filter

The simplest active low pass filter is a first-order design, consisting of an RC network followed by a non-inverting op-amp configuration. The transfer function H(s) of this circuit is derived as:

$$ H(s) = \frac{V_{out}(s)}{V_{in}(s)} = \left(1 + \frac{R_f}{R_i}\right) \cdot \frac{1}{1 + sRC} $$

Here, Rf and Ri set the DC gain A0, while R and C determine the cutoff frequency fc:

$$ f_c = \frac{1}{2\pi RC} $$

The Bode plot of this filter shows a -20 dB/decade roll-off above fc, characteristic of first-order systems. The op-amp's bandwidth must exceed fc to avoid signal degradation.

Second-Order Active Low Pass Filter

For steeper roll-off, second-order active filters are employed. The Sallen-Key topology is a common implementation, using two RC pairs and an op-amp configured as a voltage follower or amplifier. Its transfer function is:

$$ H(s) = \frac{A_0}{1 + s\left(\frac{R_1C_1 + R_2C_1 + R_1C_2(1 - A_0)\right) + s^2R_1R_2C_1C_2} $$

Where A0 is the DC gain set by the feedback network. The quality factor Q and cutoff frequency are:

$$ Q = \frac{\sqrt{R_1R_2C_1C_2}}{R_1C_1 + R_2C_1 + R_1C_2(1 - A_0)} $$ $$ f_c = \frac{1}{2\pi\sqrt{R_1R_2C_1C_2}} $$

Proper selection of component values ensures a Butterworth, Chebyshev, or Bessel response, depending on the application's need for flat passband, sharp transition, or phase linearity.

Higher-Order Filters

Cascading multiple second-order stages achieves higher-order filtering. For instance, a fourth-order filter can be constructed by cascading two second-order Sallen-Key circuits. Each stage's Q and fc must be carefully tuned to avoid peaking and maintain stability. The overall transfer function becomes the product of individual stage responses:

$$ H(s) = H_1(s) \cdot H_2(s) \cdot \ldots \cdot H_n(s) $$

Active filters with orders beyond four are practical but require precision components to mitigate cumulative errors from op-amp non-idealities like finite gain-bandwidth product and slew rate.

Design Considerations

Key parameters in active filter design include:

Modern active filters often integrate programmable components (e.g., digital potentiometers or switched capacitors) for adjustable cutoff frequencies in adaptive systems.

Active Low Pass Filter Circuits Side-by-side schematics of first-order and Sallen-Key active low pass filter configurations with labeled components and cutoff frequency formulas. Vin R C Rf Vout f_c = 1 / (2πRC) First-Order Vin R1 R2 C1 Ri C2 Vout f_c = 1 / (2π√(R1R2C1C2)) Sallen-Key
Diagram Description: The section describes circuit topologies (first-order, Sallen-Key) and their transfer functions, which are inherently spatial and require visualization of component connections.

First-Order vs. Second-Order Filters

Transfer Function and Frequency Response

The fundamental distinction between first-order and second-order low-pass filters lies in their transfer functions and roll-off rates. A first-order filter has a transfer function given by:

$$ H(s) = \frac{1}{1 + \frac{s}{\omega_c}} $$

where s is the complex frequency variable and ωc is the cutoff frequency. The magnitude response decays at −20 dB/decade beyond the cutoff frequency.

In contrast, a second-order filter has a transfer function:

$$ H(s) = \frac{1}{1 + \frac{s}{Q \omega_c} + \left(\frac{s}{\omega_c}\right)^2} $$

where Q is the quality factor, influencing the filter's resonance and damping. The roll-off rate is −40 dB/decade, providing steeper attenuation.

Pole-Zero Analysis

First-order filters have a single pole at s = −ωc, resulting in a smooth, monotonic frequency response. Second-order filters, however, exhibit complex conjugate poles when Q > 0.5, leading to peaking near the cutoff frequency. The pole locations are determined by:

$$ s = -\frac{\omega_c}{2Q} \pm j \omega_c \sqrt{1 - \frac{1}{4Q^2}} $$

Higher Q values increase resonance, while lower values (Q < 0.5) result in overdamped behavior with two real poles.

Phase Response and Group Delay

First-order filters introduce a phase shift of −90° at high frequencies, with a gradual transition. Second-order filters exhibit a phase shift of −180°, but the transition is steeper and influenced by Q. The group delay, defined as the negative derivative of phase with respect to frequency, is more pronounced in second-order filters, particularly near resonance.

Practical Implementation

First-order filters are typically implemented using a single resistor-capacitor (RC) network, making them simple and cost-effective. Second-order filters require additional components, such as inductors or active elements (e.g., op-amps), to achieve the desired response. Common topologies include:

Applications and Trade-offs

First-order filters are suitable for applications requiring minimal component count and moderate roll-off, such as basic signal conditioning. Second-order filters are preferred in scenarios demanding sharper attenuation, such as anti-aliasing in ADCs or noise suppression in RF circuits. However, they introduce trade-offs in terms of complexity, component tolerance sensitivity, and potential stability issues in active implementations.

Design Considerations

When selecting between first-order and second-order filters, key considerations include:

First-Order vs. Second-Order Filter Responses A comparison of Bode plots and pole-zero diagrams for first-order and second-order low-pass filters, showing magnitude and phase responses. First-Order Filter Magnitude (dB) Frequency (ω) ω_c -20 dB/decade Phase (deg) ω_c -90° Pole-Zero Plot Pole Second-Order Filter Magnitude (dB) Frequency (ω) ω_c -40 dB/decade Phase (deg) ω_c -180° Pole-Zero Plot Pole Pole Q factor
Diagram Description: The section compares frequency responses and pole-zero plots of first-order vs. second-order filters, which are inherently visual concepts.

3. Component Selection (Resistors, Capacitors, Op-Amps)

3.1 Component Selection (Resistors, Capacitors, Op-Amps)

The performance of a low-pass filter (LPF) is critically dependent on the choice of passive and active components. Key parameters such as cutoff frequency, phase response, and signal integrity are directly influenced by resistor and capacitor tolerances, op-amp bandwidth, and noise characteristics.

Resistor Selection

Resistors in an LPF define the time constant τ = RC, which determines the cutoff frequency fc. For a first-order passive RC filter:

$$ f_c = \frac{1}{2\pi RC} $$

Key considerations for resistor selection include:

For high-frequency applications, parasitic inductance (Lpar) becomes significant. Thin-film SMD resistors (e.g., 0603 or 0402 packages) minimize parasitic effects.

Capacitor Selection

Capacitors introduce frequency-dependent impedance ZC = 1/(jωC). The choice of dielectric material impacts stability and losses:

Voltage derating (operating at ≤80% of rated voltage) improves longevity. For second-order filters, capacitor matching (±1% or better) ensures balanced pole placement.

Operational Amplifier Selection

Active LPFs rely on op-amps to provide gain and buffer stages. Critical op-amp parameters include:

For example, a Butterworth LPF with fc = 10 kHz and Vpeak = 5 V requires:

$$ SR > 2\pi \times 10^4 \times 5 \approx 0.314 \, \text{V/μs} $$

Precision op-amps like the OPA1611 (GBW = 40 MHz, SR = 20 V/μs) are suitable for high-fidelity applications, whereas low-power designs may use the LTC6258 (GBW = 12.5 MHz, SR = 5 V/μs).

Practical Design Example

Consider a Sallen-Key second-order LPF with fc = 1 kHz and Q = 0.707 (Butterworth response). Component values are derived as:

$$ R_1 = R_2 = R = 10 \, \text{kΩ}, \quad C_1 = C_2 = C = \frac{1}{2\pi f_c R} \approx 15.9 \, \text{nF} $$

Using 1% tolerance metal-film resistors (10 kΩ) and C0G ceramic capacitors (16 nF) ensures fc accuracy within ±2%. An op-amp with GBW > 1 MHz (e.g., TL072) suffices for this application.

This section provides a rigorous, application-focused guide to component selection for low-pass filters, balancing theoretical foundations with practical design constraints. The mathematical derivations and real-world examples cater to advanced readers while maintaining readability through structured explanations.

Transfer Function and Bode Plots

Transfer Function of a Low-Pass Filter

The transfer function H(s) of a low-pass filter characterizes its frequency response in the Laplace domain. For a first-order RC low-pass filter, the transfer function is derived from the voltage divider principle:

$$ V_{out}(s) = \frac{Z_C}{Z_R + Z_C} V_{in}(s) $$

where ZC = 1/(sC) is the impedance of the capacitor and ZR = R is the resistor's impedance. Substituting these yields:

$$ H(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{1/(sC)}{R + 1/(sC)} = \frac{1}{1 + sRC} $$

The pole frequency ωc = 1/(RC) defines the cutoff frequency. Rewriting H(s) in standard form:

$$ H(s) = \frac{1}{1 + s/\omega_c} $$

Frequency Response and Bode Plots

To analyze the filter's behavior in the frequency domain, substitute s = jω:

$$ H(j\omega) = \frac{1}{1 + j\omega/\omega_c} $$

The magnitude response |H(jω)| and phase response ∠H(jω) are:

$$ |H(j\omega)| = \frac{1}{\sqrt{1 + (\omega/\omega_c)^2}} $$
$$ \angle H(j\omega) = -\tan^{-1}(\omega/\omega_c) $$

A Bode plot visualizes these responses using logarithmic scales. The magnitude plot (in dB) has two asymptotic regions:

The phase plot transitions from 0° to -90°, with -45° at ω = ωc.

Second-Order Low-Pass Filters

For a second-order RLC filter, the transfer function includes a damping factor ζ and resonant frequency ω0:

$$ H(s) = \frac{\omega_0^2}{s^2 + 2\zeta\omega_0 s + \omega_0^2} $$

The Bode plot shows a steeper -40 dB/decade rolloff above ω0, with peaking near ω0 if ζ < 0.707.

Practical Applications

Bode plots are indispensable for:

First-Order Low-Pass Filter Bode Plot Bode plot showing the magnitude (in dB) and phase (in degrees) responses of a first-order low-pass filter, with cutoff frequency ω_c, asymptotes, and key markers. Frequency (log scale) Magnitude (dB) 0 dB -20 dB/decade ω_c -3 dB Phase (degrees) 0° -45° -90° ω_c
Diagram Description: The Bode plot's magnitude and phase responses with their asymptotic behaviors and transition regions are highly visual concepts that are difficult to grasp fully from equations alone.

3.3 Practical Design Considerations

When designing a low pass filter (LPF), theoretical transfer functions must be reconciled with real-world component behavior. Non-idealities such as parasitic capacitance, inductor series resistance, and op-amp bandwidth limitations significantly alter performance.

Component Tolerances and Temperature Effects

Passive components exhibit manufacturing tolerances (typically ±5% for resistors, ±10% for capacitors). For a second-order active LPF with cutoff frequency fc:

$$ f_c = \frac{1}{2\pi\sqrt{R_1R_2C_1C_2}} $$

A 10% tolerance in both R and C can shift fc by ±20%. Temperature coefficients further exacerbate this:

Op-Amp Limitations

The finite gain-bandwidth product (GBW) of operational amplifiers imposes practical constraints. For an active LPF using a non-ideal op-amp:

$$ H(s) = \frac{A_{OL}}{1 + A_{OL}\beta(s)} $$

where AOL is the open-loop gain and β(s) the feedback factor. To maintain stability:

$$ GBW \geq 10 \times f_c \times Q^2 $$

For a Butterworth filter (Q=0.707) with fc=10 kHz, GBW must exceed 50 MHz.

PCB Layout Considerations

Parasitic capacitance between traces (Cp ≈ 0.2-1 pF/cm) and inductance of component leads (Lp ≈ 1-10 nH) create unintended poles. Mitigation strategies include:

Power Supply Rejection

Active filters require clean power rails. Power supply rejection ratio (PSRR) of modern op-amps degrades above 10 kHz. A bypass capacitor network is essential:

$$ Z_{bypass} = \frac{1}{2\pi f (C_{bulk} + C_{ceramic})} $$

Typical values: 10 µF tantalum (bulk) + 100 nF X7R (high-frequency).

Noise Analysis

Thermal noise from resistors and voltage noise from op-amps contribute to the output noise spectral density:

$$ e_n^2 = 4kTR + e_{n,opamp}^2 \left(1 + \frac{R_f}{R_g}\right)^2 $$

For a 1 kΩ resistor at 25°C, 4kTR = 16 nV/√Hz. Low-noise design requires:

4. Signal Processing and Noise Reduction

4.1 Signal Processing and Noise Reduction

Low-pass filters (LPFs) are fundamental in signal processing for attenuating high-frequency noise while preserving the integrity of low-frequency signals. Their operation is rooted in the frequency-dependent impedance characteristics of reactive components—capacitors and inductors. The simplest first-order RC LPF has a transfer function H(f) given by:

$$ H(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j \left( \frac{f}{f_c} \right)} $$

where fc is the cutoff frequency, defined as:

$$ f_c = \frac{1}{2\pi RC} $$

For noise reduction, the filter's roll-off rate is critical. A first-order LPF provides -20 dB/decade attenuation beyond fc, while higher-order filters (e.g., Butterworth, Chebyshev) achieve steeper roll-offs. The Butterworth filter, for instance, maximizes flatness in the passband with a transfer function magnitude:

$$ |H(f)| = \frac{1}{\sqrt{1 + \left( \frac{f}{f_c} \right)^{2n}}} $$

where n is the filter order. Practical implementations often use active filters (e.g., Sallen-Key topology) to avoid loading effects and improve Q-factor.

Noise Reduction Mechanisms

LPFs suppress noise by exploiting the spectral separation between signal and noise. Key considerations include:

Design Trade-offs

Filter design involves balancing:

Practical Applications

LPFs are ubiquitous in:

Frequency Response of a 4th-Order Butterworth LPF -80 dB/decade roll-off
Frequency Response of a 4th-Order Butterworth LPF Bode plot showing the frequency response of a 4th-order Butterworth low-pass filter, with labeled cutoff frequency and roll-off slope. Frequency (Hz) Magnitude (dB) 10⁰ 10¹ 10² 10³ 10⁴ 10⁵ 10⁶ 10⁷ 0 -20 -40 -60 -80 -100 f_c -80 dB/decade Passband Stopband
Diagram Description: The diagram would physically show the frequency response curve of a 4th-order Butterworth LPF with labeled roll-off rate and cutoff frequency.

Low Pass Filters in Audio Systems and Communication

:

Frequency Response in Audio Applications

In audio systems, low pass filters (LPFs) are critical for bandwidth limiting and anti-aliasing. The human auditory range spans 20 Hz to 20 kHz, but practical systems often restrict bandwidth to minimize noise and distortion. A first-order RC LPF with cutoff frequency fc is defined by:

$$ f_c = \frac{1}{2\pi RC} $$

For high-fidelity audio, higher-order filters (Butterworth, Chebyshev) are preferred due to their steeper roll-off. A second-order Butterworth LPF, for instance, attenuates signals at −40 dB/decade beyond fc, given by:

$$ H(s) = \frac{\omega_c^2}{s^2 + \sqrt{2}\omega_c s + \omega_c^2} $$

Phase Linearity and Group Delay

LPFs introduce phase shifts, which can distort transient signals like percussion. A Bessel filter preserves phase linearity, sacrificing roll-off steepness. The group delay τg, defined as the negative derivative of phase with respect to angular frequency, is nearly constant for Bessel filters:

$$ \tau_g = -\frac{d\phi}{d\omega} $$

Communication Systems: Channel Noise and ISI

In RF and wired communication, LPFs mitigate inter-symbol interference (ISI) by band-limiting transmitted signals. The raised-cosine filter, a hybrid LPF, minimizes ISI while optimizing spectral efficiency. Its transfer function combines an LPF with a tunable roll-off factor α:

$$ H(f) = \begin{cases} 1, & |f| \leq \frac{1 - \alpha}{2T} \\ \frac{1}{2}\left[1 + \cos\left(\frac{\pi T}{\alpha}\left(|f| - \frac{1 - \alpha}{2T}\right)\right)\right], & \frac{1 - \alpha}{2T} \leq |f| \leq \frac{1 + \alpha}{2T} \\ 0, & \text{otherwise} \end{cases} $$

Practical Implementation: Active vs. Passive Filters

Active LPFs using op-amps (e.g., Sallen-Key topology) avoid loading effects and provide gain. For instance, a Sallen-Key second-order LPF with unity gain has:

$$ f_c = \frac{1}{2\pi \sqrt{R_1 R_2 C_1 C_2}} $$

Passive LC filters, however, are favored in high-power RF applications due to their linearity and lack of active noise sources.

Case Study: LPF in Digital Audio Workstations (DAWs)

Modern DAWs use FIR-based LPFs with linear phase for mastering. An FIR filter of order N applies convolution:

$$ y[n] = \sum_{k=0}^{N} h[k] \cdot x[n-k] $$

where h[k] are coefficients designed via windowing or Parks-McClellan optimization.

Frequency Response and Phase Characteristics of LPFs Bode plot showing the magnitude (dB) and phase (degrees) response of a low-pass filter, including cutoff frequency, roll-off slopes, and group delay. Frequency (log scale) Magnitude Response (dB) 0 f_c -20 dB/decade -40 dB/decade Phase Response (degrees) 0 Nonlinear phase Linear phase τ_g
Diagram Description: The section covers frequency response, phase shifts, and filter transfer functions which are inherently visual concepts.

4.3 Power Supply Filtering

Power supply noise, often manifesting as high-frequency ripple or transient disturbances, degrades the performance of sensitive analog and digital circuits. A low-pass filter (LPF) is critical in attenuating this noise while preserving the DC component of the supply voltage. The design parameters—cutoff frequency, roll-off slope, and component selection—directly impact the filter's efficacy.

Transfer Function and Impedance Considerations

The LPF for power supplies typically employs an RC or LC topology. The transfer function for an RC filter is:

$$ H(s) = \frac{1}{1 + sRC} $$

where R represents the equivalent series resistance (ESR) of the capacitor, and C is the filtering capacitance. For an LC filter, the transfer function becomes:

$$ H(s) = \frac{1}{1 + s\frac{L}{R_{load}} + s^2LC} $$

The LC configuration offers a steeper roll-off (−40 dB/decade) compared to the RC filter (−20 dB/decade), but requires careful damping to avoid resonance peaks. The quality factor (Q) must be minimized to prevent ringing:

$$ Q = \frac{1}{2} \sqrt{\frac{L}{C}} \cdot \frac{1}{R_{load} + R_{ESR}} $$

Component Selection and Practical Trade-offs

Key considerations include:

A multi-stage approach is common in high-performance systems. For example, a bulk electrolytic capacitor (10–100 µF) handles low-frequency ripple, while a ceramic capacitor (0.1–1 µF) suppresses high-frequency noise.

Real-World Applications

In switch-mode power supplies (SMPS), a second-stage LPF with a cutoff frequency below the switching frequency (e.g., 50 kHz for a 200 kHz SMPS) is essential. For precision analog circuits (e.g., ADCs or oscillators), a ferrite bead in series with a capacitor forms a broadband filter, attenuating both conducted and radiated interference.

LC Power Supply Filter

Modern integrated voltage regulators (e.g., LDOs) often embed active filtering, but discrete LPFs remain necessary for high-current or ultra-low-noise scenarios. SPICE simulations are recommended to validate the design under transient and load-variation conditions.

5. Key Textbooks and Papers

5.1 Key Textbooks and Papers

5.2 Online Resources and Tutorials

5.3 Advanced Topics for Further Study