Magnetic Amplifiers

1. Basic Principles and Operation

1.1 Basic Principles and Operation

Core Mechanism of Magnetic Amplifiers

A magnetic amplifier (mag amp) operates by exploiting the nonlinear B-H hysteresis characteristics of ferromagnetic materials. The device consists of a saturable reactor with at least two windings: a control winding (DC bias) and an AC winding (load current). The amplification effect arises from the controlled saturation of the core, which modulates the effective impedance of the AC winding.

Mathematical Derivation of Gain

The voltage-current relationship in the AC winding is governed by Faraday's law and the core's magnetic properties. For a sinusoidal input voltage VAC:

$$ V_{AC} = N_{AC} \frac{d\Phi}{dt} $$

where NAC is the number of turns in the AC winding, and Φ is the magnetic flux. The core's permeability μ varies with the DC control current IDC:

$$ \mu(I_{DC}) = \mu_0 \mu_r \left(1 - \frac{I_{DC}}{I_{sat}}\right) $$

where Isat is the saturation current. The effective inductance L of the AC winding is:

$$ L = \frac{N_{AC}^2 \mu(I_{DC}) A_c}{l_c} $$

with Ac and lc being the core's cross-sectional area and magnetic path length, respectively. The gain G is derived from the ratio of output power (AC winding) to input power (control winding):

$$ G \propto \frac{N_{AC}^2}{N_{DC}^2} \cdot \frac{\mu(I_{DC})}{R_{load}} $$

Key Operating Modes

Practical Implementation Considerations

Core material selection critically impacts performance. Grain-oriented silicon steel offers high permeability and sharp saturation characteristics, while ferrites provide faster response times. Modern designs often incorporate feedback windings to improve linearity and reduce hysteresis losses. The typical frequency range spans 50 Hz to 20 kHz, with power handling from milliwatts to several kilowatts.

Control Winding (DC) AC Winding Core

Historical Context and Modern Applications

First developed in the early 20th century, magnetic amplifiers saw extensive use in power regulation before being largely supplanted by semiconductor devices. Contemporary applications include:

The inherent galvanic isolation and overload tolerance make mag amps suitable for harsh environments where solid-state devices would fail. Recent advances in nanocrystalline alloys have revived interest in magnetic amplification for high-efficiency power conversion.

Magnetic Amplifier Core Windings Configuration A schematic diagram showing the core structure with control and AC windings, their spatial arrangement around the saturable core, and the directional relationship between DC bias and AC modulation. Includes a simplified B-H hysteresis curve overlay. Core Control Winding (DC) AC Winding Magnetic Flux Path B-H Curve H B DC Bias AC Modulation
Diagram Description: The diagram would physically show the core structure with control and AC windings, their spatial arrangement around the saturable core, and the directional relationship between DC bias and AC modulation.

1.2 Core Materials and Their Properties

Magnetic Core Characteristics

The performance of a magnetic amplifier is critically dependent on the core material's magnetic properties. The most important parameters include:

The relationship between flux density (B) and magnetic field intensity (H) is described by the hysteresis loop, which determines energy losses:

$$ W_h = \oint H \, dB $$

Common Core Materials

Silicon Steel (Electrical Steel)

Silicon steel, typically containing 3–5% silicon, is widely used due to its balanced properties:

The addition of silicon increases resistivity, reducing eddy current losses. Grain-oriented silicon steel exhibits anisotropic properties, with superior performance along the rolling direction.

Nickel-Iron Alloys (Permalloy)

Nickel-iron alloys (e.g., 80% Ni, 20% Fe) offer extremely high permeability (μr up to 100,000) but lower saturation flux density (~0.8 T). These are used in:

The permeability of permalloy is highly dependent on heat treatment and annealing processes.

Amorphous and Nanocrystalline Alloys

Modern amorphous metals (e.g., Metglas) and nanocrystalline materials provide:

These materials are produced through rapid solidification techniques, resulting in a non-crystalline structure that minimizes domain wall pinning.

Core Losses and Frequency Dependence

Total core losses (Pcore) consist of hysteresis losses (Ph) and eddy current losses (Pe):

$$ P_{core} = P_h + P_e = k_h f B^\alpha + k_e f^2 B^2 $$

where:

At higher frequencies (>10 kHz), eddy current losses dominate, making high-resistivity materials essential.

Practical Selection Criteria

When selecting core materials for magnetic amplifiers, engineers must consider:

Recent advances in nanocrystalline materials have enabled magnetic amplifiers to operate at higher efficiencies and power densities, particularly in switched-mode power supplies and renewable energy systems.

Magnetic Hysteresis Loop A B-H hysteresis loop showing the relationship between flux density (B) and magnetic field intensity (H), including saturation points (B_sat) and coercivity (H_c). B H -Bₛₐₜ +Bₛₐₜ -H_c +H_c +Bₛₐₜ -Bₛₐₜ +H_c -H_c μ (slope) Magnetization Direction
Diagram Description: The diagram would show the B-H hysteresis loop to visually represent the relationship between flux density and magnetic field intensity, including key points like saturation and coercivity.

1.2 Core Materials and Their Properties

Magnetic Core Characteristics

The performance of a magnetic amplifier is critically dependent on the core material's magnetic properties. The most important parameters include:

The relationship between flux density (B) and magnetic field intensity (H) is described by the hysteresis loop, which determines energy losses:

$$ W_h = \oint H \, dB $$

Common Core Materials

Silicon Steel (Electrical Steel)

Silicon steel, typically containing 3–5% silicon, is widely used due to its balanced properties:

The addition of silicon increases resistivity, reducing eddy current losses. Grain-oriented silicon steel exhibits anisotropic properties, with superior performance along the rolling direction.

Nickel-Iron Alloys (Permalloy)

Nickel-iron alloys (e.g., 80% Ni, 20% Fe) offer extremely high permeability (μr up to 100,000) but lower saturation flux density (~0.8 T). These are used in:

The permeability of permalloy is highly dependent on heat treatment and annealing processes.

Amorphous and Nanocrystalline Alloys

Modern amorphous metals (e.g., Metglas) and nanocrystalline materials provide:

These materials are produced through rapid solidification techniques, resulting in a non-crystalline structure that minimizes domain wall pinning.

Core Losses and Frequency Dependence

Total core losses (Pcore) consist of hysteresis losses (Ph) and eddy current losses (Pe):

$$ P_{core} = P_h + P_e = k_h f B^\alpha + k_e f^2 B^2 $$

where:

At higher frequencies (>10 kHz), eddy current losses dominate, making high-resistivity materials essential.

Practical Selection Criteria

When selecting core materials for magnetic amplifiers, engineers must consider:

Recent advances in nanocrystalline materials have enabled magnetic amplifiers to operate at higher efficiencies and power densities, particularly in switched-mode power supplies and renewable energy systems.

Magnetic Hysteresis Loop A B-H hysteresis loop showing the relationship between flux density (B) and magnetic field intensity (H), including saturation points (B_sat) and coercivity (H_c). B H -Bₛₐₜ +Bₛₐₜ -H_c +H_c +Bₛₐₜ -Bₛₐₜ +H_c -H_c μ (slope) Magnetization Direction
Diagram Description: The diagram would show the B-H hysteresis loop to visually represent the relationship between flux density and magnetic field intensity, including key points like saturation and coercivity.

1.3 Comparison with Electronic Amplifiers

Fundamental Operating Principles

Magnetic amplifiers (magamps) and electronic amplifiers (e.g., vacuum tubes, transistors) achieve signal amplification through fundamentally different mechanisms. Magamps rely on nonlinear inductance in saturable reactors, where a small DC control current modulates the core's permeability, altering the AC load current. In contrast, electronic amplifiers use active devices (transistors or tubes) to directly modulate electron flow via voltage or current inputs. The gain in magamps is derived from the ratio of load power to control power, whereas electronic amplifiers exhibit voltage/current gain defined by device parameters like transconductance (gm) or current gain (β).

Efficiency and Power Handling

Magamps excel in high-power applications (e.g., industrial control, aerospace) due to their absence of semiconductor junctions, enabling operation at kilowatt levels with minimal heat dissipation. Their efficiency (η) is governed by core losses (hysteresis, eddy currents) and can exceed 90% in optimized designs. Electronic amplifiers, particularly class-AB or class-D, achieve comparable efficiency only at lower frequencies and suffer from switching losses in high-power regimes. For instance, a magamp handling 10 kW at 400 Hz may exhibit η ≈ 92%, while a silicon IGBT-based amplifier at the same power typically reaches η ≈ 85%.

$$ \eta_{\text{magamp}} = \frac{P_{\text{load}}}{P_{\text{load}} + P_{\text{core}} + P_{\text{copper}}} $$

Frequency Response and Bandwidth

The bandwidth of magamps is intrinsically limited by the core's magnetic relaxation time (τ = L/R), restricting operation to sub-100 kHz frequencies. Electronic amplifiers, however, leverage fast carrier mobility (e.g., electron drift in semiconductors) to achieve gigahertz bandwidths. For example, a push-pull BJT amplifier can deliver flat response from DC to 100 MHz, while a magamp's response rolls off beyond 10 kHz due to core saturation dynamics:

$$ f_{\text{max}} = \frac{1}{2\pi \sqrt{L_{\text{sat}} C_{\text{stray}}} $$

Noise and Distortion Characteristics

Magamps exhibit lower thermal noise than electronic amplifiers, as they lack shot noise (from semiconductor junctions) and flicker noise. However, they introduce harmonic distortion from core hysteresis, quantified by the total harmonic distortion (THD) metric. A typical magamp may show THD < 2% at 60 Hz, while a low-noise op-amp (e.g., LT1028) achieves THD < 0.0003% at 1 kHz. The noise figure (NF) of magamps is dominated by Barkhausen noise from domain wall motion, whereas electronic amplifiers contend with Johnson-Nyquist noise.

Reliability and Environmental Robustness

The solid-state nature of magamps (no moving parts or fragile cathodes) grants them superior reliability in extreme environments. They are immune to ionizing radiation, EMP, and temperature extremes (−55°C to +200°C for ferrite cores), outperforming semiconductor amplifiers. Case studies in nuclear power control systems show magamp MTBF exceeding 500,000 hours, compared to 100,000 hours for radiation-hardened MOSFET amplifiers.

Modern Hybrid Architectures

Contemporary designs often combine magamps with electronic components to leverage both technologies. For instance, magamp-post-regulated switch-mode power supplies use a magamp for precise secondary-side voltage control, while MOSFETs handle high-frequency switching. This hybrid approach achieves efficiencies of 94% with ripple < 10 mV, as demonstrated in aerospace power systems like the Boeing 787's auxiliary power units.

Control Winding Load Winding
Magamp vs Electronic Amplifier Core Structures A schematic comparison of magnetic amplifier (left) and electronic amplifier (right) core structures, showing key components and signal paths. Magamp vs Electronic Amplifier Core Structures Magnetic Amplifier Control Winding Load Winding Core Saturation Input Output Electronic Amplifier Base (B) Emitter (E) Collector (C) Input Output Power Supply
Diagram Description: A diagram would visually contrast the core structures and signal paths of magnetic amplifiers versus electronic amplifiers, showing their fundamental differences in component arrangement and energy flow.

1.3 Comparison with Electronic Amplifiers

Fundamental Operating Principles

Magnetic amplifiers (magamps) and electronic amplifiers (e.g., vacuum tubes, transistors) achieve signal amplification through fundamentally different mechanisms. Magamps rely on nonlinear inductance in saturable reactors, where a small DC control current modulates the core's permeability, altering the AC load current. In contrast, electronic amplifiers use active devices (transistors or tubes) to directly modulate electron flow via voltage or current inputs. The gain in magamps is derived from the ratio of load power to control power, whereas electronic amplifiers exhibit voltage/current gain defined by device parameters like transconductance (gm) or current gain (β).

Efficiency and Power Handling

Magamps excel in high-power applications (e.g., industrial control, aerospace) due to their absence of semiconductor junctions, enabling operation at kilowatt levels with minimal heat dissipation. Their efficiency (η) is governed by core losses (hysteresis, eddy currents) and can exceed 90% in optimized designs. Electronic amplifiers, particularly class-AB or class-D, achieve comparable efficiency only at lower frequencies and suffer from switching losses in high-power regimes. For instance, a magamp handling 10 kW at 400 Hz may exhibit η ≈ 92%, while a silicon IGBT-based amplifier at the same power typically reaches η ≈ 85%.

$$ \eta_{\text{magamp}} = \frac{P_{\text{load}}}{P_{\text{load}} + P_{\text{core}} + P_{\text{copper}}} $$

Frequency Response and Bandwidth

The bandwidth of magamps is intrinsically limited by the core's magnetic relaxation time (τ = L/R), restricting operation to sub-100 kHz frequencies. Electronic amplifiers, however, leverage fast carrier mobility (e.g., electron drift in semiconductors) to achieve gigahertz bandwidths. For example, a push-pull BJT amplifier can deliver flat response from DC to 100 MHz, while a magamp's response rolls off beyond 10 kHz due to core saturation dynamics:

$$ f_{\text{max}} = \frac{1}{2\pi \sqrt{L_{\text{sat}} C_{\text{stray}}} $$

Noise and Distortion Characteristics

Magamps exhibit lower thermal noise than electronic amplifiers, as they lack shot noise (from semiconductor junctions) and flicker noise. However, they introduce harmonic distortion from core hysteresis, quantified by the total harmonic distortion (THD) metric. A typical magamp may show THD < 2% at 60 Hz, while a low-noise op-amp (e.g., LT1028) achieves THD < 0.0003% at 1 kHz. The noise figure (NF) of magamps is dominated by Barkhausen noise from domain wall motion, whereas electronic amplifiers contend with Johnson-Nyquist noise.

Reliability and Environmental Robustness

The solid-state nature of magamps (no moving parts or fragile cathodes) grants them superior reliability in extreme environments. They are immune to ionizing radiation, EMP, and temperature extremes (−55°C to +200°C for ferrite cores), outperforming semiconductor amplifiers. Case studies in nuclear power control systems show magamp MTBF exceeding 500,000 hours, compared to 100,000 hours for radiation-hardened MOSFET amplifiers.

Modern Hybrid Architectures

Contemporary designs often combine magamps with electronic components to leverage both technologies. For instance, magamp-post-regulated switch-mode power supplies use a magamp for precise secondary-side voltage control, while MOSFETs handle high-frequency switching. This hybrid approach achieves efficiencies of 94% with ripple < 10 mV, as demonstrated in aerospace power systems like the Boeing 787's auxiliary power units.

Control Winding Load Winding
Magamp vs Electronic Amplifier Core Structures A schematic comparison of magnetic amplifier (left) and electronic amplifier (right) core structures, showing key components and signal paths. Magamp vs Electronic Amplifier Core Structures Magnetic Amplifier Control Winding Load Winding Core Saturation Input Output Electronic Amplifier Base (B) Emitter (E) Collector (C) Input Output Power Supply
Diagram Description: A diagram would visually contrast the core structures and signal paths of magnetic amplifiers versus electronic amplifiers, showing their fundamental differences in component arrangement and energy flow.

2. Core Geometry and Windings

2.1 Core Geometry and Windings

The performance of a magnetic amplifier is critically dependent on the geometry of its core and the configuration of its windings. The core material, shape, and winding arrangement dictate the amplifier's saturation characteristics, efficiency, and frequency response.

Core Material and Geometry

The core of a magnetic amplifier is typically constructed from high-permeability, low-hysteresis materials such as grain-oriented silicon steel, nickel-iron alloys (e.g., Permalloy), or amorphous metallic glass. The core geometry influences the magnetic path length (lm) and cross-sectional area (Ac), which directly affect inductance and saturation behavior.

$$ L = \frac{N^2 \mu_0 \mu_r A_c}{l_m} $$

where:

Toroidal cores are often preferred due to their closed magnetic path, minimizing flux leakage and external interference. Laminated cores reduce eddy current losses, while tape-wound cores enhance high-frequency performance.

Winding Configurations

The windings in a magnetic amplifier consist of at least two coils: a control winding and an AC (load) winding. The control winding is driven by a DC or low-frequency signal, while the AC winding carries the amplified output. The turns ratio (Nc/Nac) determines the gain and coupling efficiency.

$$ V_{out} = V_{in} \left( \frac{N_{ac}}{N_c} \right) \cdot \frac{d\Phi}{dt} $$

where dΦ/dt is the rate of change of magnetic flux, controlled by the saturation state of the core.

Bifilar winding techniques are sometimes employed to improve coupling and reduce parasitic capacitance. The winding resistance (Rw) and leakage inductance (Ll) must be minimized to prevent power losses and phase distortion.

Practical Considerations

In high-power applications, forced air or liquid cooling may be necessary to manage thermal losses. Core stacking and interleaved windings help distribute heat and reduce hotspots. The choice of insulation materials (e.g., Nomex, Mylar) is crucial for high-voltage isolation and thermal stability.

Modern magnetic amplifiers often use nanocrystalline cores for superior frequency response and reduced core losses. The geometry is optimized using finite element analysis (FEA) to balance magnetic efficiency, thermal performance, and physical size constraints.

2.1 Core Geometry and Windings

The performance of a magnetic amplifier is critically dependent on the geometry of its core and the configuration of its windings. The core material, shape, and winding arrangement dictate the amplifier's saturation characteristics, efficiency, and frequency response.

Core Material and Geometry

The core of a magnetic amplifier is typically constructed from high-permeability, low-hysteresis materials such as grain-oriented silicon steel, nickel-iron alloys (e.g., Permalloy), or amorphous metallic glass. The core geometry influences the magnetic path length (lm) and cross-sectional area (Ac), which directly affect inductance and saturation behavior.

$$ L = \frac{N^2 \mu_0 \mu_r A_c}{l_m} $$

where:

Toroidal cores are often preferred due to their closed magnetic path, minimizing flux leakage and external interference. Laminated cores reduce eddy current losses, while tape-wound cores enhance high-frequency performance.

Winding Configurations

The windings in a magnetic amplifier consist of at least two coils: a control winding and an AC (load) winding. The control winding is driven by a DC or low-frequency signal, while the AC winding carries the amplified output. The turns ratio (Nc/Nac) determines the gain and coupling efficiency.

$$ V_{out} = V_{in} \left( \frac{N_{ac}}{N_c} \right) \cdot \frac{d\Phi}{dt} $$

where dΦ/dt is the rate of change of magnetic flux, controlled by the saturation state of the core.

Bifilar winding techniques are sometimes employed to improve coupling and reduce parasitic capacitance. The winding resistance (Rw) and leakage inductance (Ll) must be minimized to prevent power losses and phase distortion.

Practical Considerations

In high-power applications, forced air or liquid cooling may be necessary to manage thermal losses. Core stacking and interleaved windings help distribute heat and reduce hotspots. The choice of insulation materials (e.g., Nomex, Mylar) is crucial for high-voltage isolation and thermal stability.

Modern magnetic amplifiers often use nanocrystalline cores for superior frequency response and reduced core losses. The geometry is optimized using finite element analysis (FEA) to balance magnetic efficiency, thermal performance, and physical size constraints.

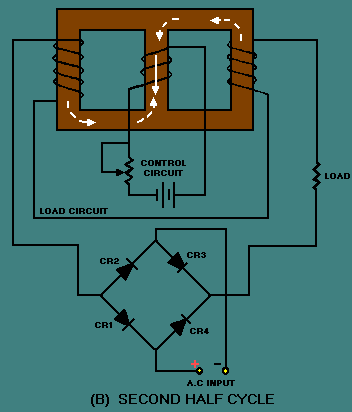
Control and Load Circuits

Control Circuit Operation

The control circuit in a magnetic amplifier regulates the output by varying the DC bias current in the control winding. The core's saturation level is modulated by the control current, which adjusts the effective impedance of the load winding. The relationship between control current \( I_c \) and load current \( I_L \) is nonlinear due to the B-H hysteresis characteristics of the core material. For small-signal analysis, the incremental gain \( G \) is derived from the slope of the transfer curve:

$$ G = \frac{\Delta I_L}{\Delta I_c} = \frac{N_c}{N_L} \cdot \frac{\mu_r \mu_0 A_e}{l_e} $$

where \( N_c \) and \( N_L \) are the turns of the control and load windings, \( \mu_r \) is the relative permeability, \( A_e \) is the effective cross-sectional area, and \( l_e \) is the magnetic path length. The control circuit's time constant \( \tau_c \) is dominated by the inductance \( L_c \) and resistance \( R_c \):

$$ \tau_c = \frac{L_c}{R_c} = \frac{N_c^2 \mu_r \mu_0 A_e}{l_e R_c} $$

Load Circuit Dynamics

The load circuit typically includes an AC supply and a rectifier (for DC applications). The load current \( I_L \) is constrained by the core's saturation flux density \( B_{sat} \):

$$ I_L \leq \frac{B_{sat} l_e}{\mu_0 \mu_r N_L} $$

In practical designs, a feedback winding is often added to linearize the response. The feedback factor \( \beta \) is defined as:

$$ \beta = \frac{N_f}{N_c} \cdot \frac{d\Phi}{dI_c} $$

where \( N_f \) is the feedback winding turns and \( \Phi \) is the magnetic flux. This introduces a closed-loop gain \( G_{cl} \):

$$ G_{cl} = \frac{G}{1 + G \beta} $$

Harmonic Distortion and Compensation

Nonlinearity in the B-H curve introduces harmonic distortion, quantified by the total harmonic distortion (THD):

$$ \text{THD} = \sqrt{\sum_{n=2}^{\infty} \left( \frac{I_{n}}{I_1} \right)^2 } $$

where \( I_n \) is the nth harmonic component. To mitigate THD, push-pull configurations or predistortion networks are employed. The latter uses a nonlinear impedance \( Z_p \) in series with the control winding to cancel core nonlinearities.

Practical Implementation

In high-power applications, thyristor-driven control circuits are common. The gate trigger angle \( \alpha \) directly influences the effective control current:

$$ I_c(\alpha) = \frac{V_{ctrl}}{R_c} \left( 1 - \frac{\alpha}{\pi} \right) $$

This method enables phase-controlled amplification, useful in motor drives and power regulation. Core materials like grain-oriented silicon steel or amorphous alloys are selected for their square B-H loops and low core losses.

Control Winding (N_c) Load Winding (N_L) Feedback Winding (N_f)
Magnetic Amplifier Winding Configuration and Core Saturation Schematic diagram showing the winding arrangement on a magnetic core and the corresponding B-H curve with operating points. Core Material N_c N_L N_f B (Flux Density) H (Field Intensity) Hysteresis Loop B_sat -B_sat μ_r ΔI_c ΔI_L
Diagram Description: The section involves complex spatial relationships between control, load, and feedback windings, and their nonlinear interactions with core saturation.

Control and Load Circuits

Control Circuit Operation

The control circuit in a magnetic amplifier regulates the output by varying the DC bias current in the control winding. The core's saturation level is modulated by the control current, which adjusts the effective impedance of the load winding. The relationship between control current \( I_c \) and load current \( I_L \) is nonlinear due to the B-H hysteresis characteristics of the core material. For small-signal analysis, the incremental gain \( G \) is derived from the slope of the transfer curve:

$$ G = \frac{\Delta I_L}{\Delta I_c} = \frac{N_c}{N_L} \cdot \frac{\mu_r \mu_0 A_e}{l_e} $$

where \( N_c \) and \( N_L \) are the turns of the control and load windings, \( \mu_r \) is the relative permeability, \( A_e \) is the effective cross-sectional area, and \( l_e \) is the magnetic path length. The control circuit's time constant \( \tau_c \) is dominated by the inductance \( L_c \) and resistance \( R_c \):

$$ \tau_c = \frac{L_c}{R_c} = \frac{N_c^2 \mu_r \mu_0 A_e}{l_e R_c} $$

Load Circuit Dynamics

The load circuit typically includes an AC supply and a rectifier (for DC applications). The load current \( I_L \) is constrained by the core's saturation flux density \( B_{sat} \):

$$ I_L \leq \frac{B_{sat} l_e}{\mu_0 \mu_r N_L} $$

In practical designs, a feedback winding is often added to linearize the response. The feedback factor \( \beta \) is defined as:

$$ \beta = \frac{N_f}{N_c} \cdot \frac{d\Phi}{dI_c} $$

where \( N_f \) is the feedback winding turns and \( \Phi \) is the magnetic flux. This introduces a closed-loop gain \( G_{cl} \):

$$ G_{cl} = \frac{G}{1 + G \beta} $$

Harmonic Distortion and Compensation

Nonlinearity in the B-H curve introduces harmonic distortion, quantified by the total harmonic distortion (THD):

$$ \text{THD} = \sqrt{\sum_{n=2}^{\infty} \left( \frac{I_{n}}{I_1} \right)^2 } $$

where \( I_n \) is the nth harmonic component. To mitigate THD, push-pull configurations or predistortion networks are employed. The latter uses a nonlinear impedance \( Z_p \) in series with the control winding to cancel core nonlinearities.

Practical Implementation

In high-power applications, thyristor-driven control circuits are common. The gate trigger angle \( \alpha \) directly influences the effective control current:

$$ I_c(\alpha) = \frac{V_{ctrl}}{R_c} \left( 1 - \frac{\alpha}{\pi} \right) $$

This method enables phase-controlled amplification, useful in motor drives and power regulation. Core materials like grain-oriented silicon steel or amorphous alloys are selected for their square B-H loops and low core losses.

Control Winding (N_c) Load Winding (N_L) Feedback Winding (N_f)
Magnetic Amplifier Winding Configuration and Core Saturation Schematic diagram showing the winding arrangement on a magnetic core and the corresponding B-H curve with operating points. Core Material N_c N_L N_f B (Flux Density) H (Field Intensity) Hysteresis Loop B_sat -B_sat μ_r ΔI_c ΔI_L
Diagram Description: The section involves complex spatial relationships between control, load, and feedback windings, and their nonlinear interactions with core saturation.

2.3 Feedback Mechanisms

Feedback in magnetic amplifiers enhances stability, linearity, and gain control by reintroducing a portion of the output signal into the input circuit. The core principle relies on the nonlinear magnetic properties of saturable reactors, where feedback modifies the effective permeability and thus the amplification characteristics.

Negative Feedback in Magnetic Amplifiers

Negative feedback reduces gain but improves bandwidth and distortion. The feedback signal opposes the input, stabilizing the amplifier against parameter variations. For a magnetic amplifier with gain A and feedback factor β, the closed-loop gain Af is:

$$ A_f = \frac{A}{1 + A\beta} $$

In practical implementations, negative feedback is achieved by winding a feedback coil on the same core as the control winding. The current in this coil generates a magnetic flux that opposes the control flux, effectively linearizing the B-H curve operation region.

Positive Feedback and Regeneration

Positive feedback increases gain and sensitivity at the cost of stability. This technique was historically used in magnetic amplifier designs for bistable operation or high-gain applications. The closed-loop gain with positive feedback becomes:

$$ A_f = \frac{A}{1 - A\beta} $$

When Aβ approaches unity, the system becomes highly sensitive to input variations, useful in switching applications. However, careful design is required to prevent unwanted oscillations.

Feedback Implementation Techniques

Three primary methods exist for implementing feedback in magnetic amplifiers:

The choice depends on whether current, voltage, or power amplification is the primary objective. Flux feedback provides the fastest response but requires precise winding alignment.

Mathematical Analysis of Feedback Effects

The incremental gain of a magnetic amplifier with feedback can be derived from the core's magnetization curve. Let μΔ represent the incremental permeability:

$$ \mu_\Delta = \frac{dB}{dH} $$

With feedback, the effective permeability μeff becomes:

$$ \mu_{eff} = \frac{\mu_\Delta}{1 \pm \mu_\Delta \beta N^2 / l} $$

where N is the number of turns and l the magnetic path length. The ± sign corresponds to negative/positive feedback respectively.

Practical Considerations

In power applications, feedback windings must handle significant currents without excessive heating. Litz wire is often used to minimize skin effect losses at higher frequencies. The feedback ratio must be carefully balanced against:

Modern implementations often combine magnetic amplifiers with semiconductor devices for improved feedback precision, using op-amps or digital controllers to maintain optimal operating points across varying conditions.

Magnetic Amplifier Feedback Winding Configuration Cross-section of a magnetic amplifier core showing control and feedback windings with flux paths and a B-H curve inset. Magnetic Core Control Winding (I_c) Feedback Winding (I_f) Resultant Flux (Φ) B-H Curve H B Input Output
Diagram Description: The diagram would show the physical winding arrangement of feedback/control coils on the core and their magnetic flux interactions, which is spatial and not fully conveyed by text.

2.3 Feedback Mechanisms

Feedback in magnetic amplifiers enhances stability, linearity, and gain control by reintroducing a portion of the output signal into the input circuit. The core principle relies on the nonlinear magnetic properties of saturable reactors, where feedback modifies the effective permeability and thus the amplification characteristics.

Negative Feedback in Magnetic Amplifiers

Negative feedback reduces gain but improves bandwidth and distortion. The feedback signal opposes the input, stabilizing the amplifier against parameter variations. For a magnetic amplifier with gain A and feedback factor β, the closed-loop gain Af is:

$$ A_f = \frac{A}{1 + A\beta} $$

In practical implementations, negative feedback is achieved by winding a feedback coil on the same core as the control winding. The current in this coil generates a magnetic flux that opposes the control flux, effectively linearizing the B-H curve operation region.

Positive Feedback and Regeneration

Positive feedback increases gain and sensitivity at the cost of stability. This technique was historically used in magnetic amplifier designs for bistable operation or high-gain applications. The closed-loop gain with positive feedback becomes:

$$ A_f = \frac{A}{1 - A\beta} $$

When Aβ approaches unity, the system becomes highly sensitive to input variations, useful in switching applications. However, careful design is required to prevent unwanted oscillations.

Feedback Implementation Techniques

Three primary methods exist for implementing feedback in magnetic amplifiers:

The choice depends on whether current, voltage, or power amplification is the primary objective. Flux feedback provides the fastest response but requires precise winding alignment.

Mathematical Analysis of Feedback Effects

The incremental gain of a magnetic amplifier with feedback can be derived from the core's magnetization curve. Let μΔ represent the incremental permeability:

$$ \mu_\Delta = \frac{dB}{dH} $$

With feedback, the effective permeability μeff becomes:

$$ \mu_{eff} = \frac{\mu_\Delta}{1 \pm \mu_\Delta \beta N^2 / l} $$

where N is the number of turns and l the magnetic path length. The ± sign corresponds to negative/positive feedback respectively.

Practical Considerations

In power applications, feedback windings must handle significant currents without excessive heating. Litz wire is often used to minimize skin effect losses at higher frequencies. The feedback ratio must be carefully balanced against:

Modern implementations often combine magnetic amplifiers with semiconductor devices for improved feedback precision, using op-amps or digital controllers to maintain optimal operating points across varying conditions.

Magnetic Amplifier Feedback Winding Configuration Cross-section of a magnetic amplifier core showing control and feedback windings with flux paths and a B-H curve inset. Magnetic Core Control Winding (I_c) Feedback Winding (I_f) Resultant Flux (Φ) B-H Curve H B Input Output
Diagram Description: The diagram would show the physical winding arrangement of feedback/control coils on the core and their magnetic flux interactions, which is spatial and not fully conveyed by text.

3. Industrial Control Systems

3.1 Industrial Control Systems

Magnetic amplifiers (magamps) have been historically significant in industrial control due to their ruggedness, reliability, and ability to handle high power levels without semiconductor components. Their operation relies on the nonlinear B-H curve of saturable reactors, enabling amplification through controlled saturation of magnetic cores.

Core Operating Principle

The gain of a magnetic amplifier is governed by the saturation characteristics of its ferromagnetic core. The control winding (input) and load winding (output) share a common magnetic path. When the control current drives the core into saturation, the impedance of the load winding drops sharply, allowing larger currents to flow.

$$ G = \frac{N_c}{N_l} \cdot \frac{\mu_{sat}}{\mu_{unsat}} $$

where G is the gain, Nc and Nl are turns of control and load windings, and μsat, μunsat are permeabilities in saturated/unsaturated states.

Feedback Stabilization

Industrial magamps often employ self-saturating circuits with rectifier feedback to improve response time and linearity. A typical configuration uses:

Core Load

Modern Applications

While largely replaced by solid-state devices, magamps persist in:

Case Study: Steel Mill Current Regulation

A 1980s-era rolling mill employed a 3-stage magamp system to regulate 1500A DC motor currents. The design achieved ±0.5% stability through:

$$ \tau = \frac{L_{core}}{R_{load}} \leq 10ms $$

where τ is the time constant, Lcore is unsaturated inductance, and Rload is motor resistance.

Advantages Over Semiconductor Drives

Parameter Magnetic Amplifier Thyristor Drive
Overload Capacity 500% for 1s 150% for 1s
MTBF >100,000 hrs 50,000 hrs
EMI Susceptibility Immune Requires filtering
Magnetic Amplifier Core Structure Schematic of a magnetic amplifier core showing ferromagnetic core with control and load windings, illustrating saturation effects on impedance. Control Input Control Return Load Output Load Return N_c (Control Turns) N_l (Load Turns) μ_sat μ_unsat Impedance: High (unsat) → Low (sat)
Diagram Description: The diagram would physically show the magnetic core with control and load windings, their spatial arrangement, and the saturation effect on impedance.

3.1 Industrial Control Systems

Magnetic amplifiers (magamps) have been historically significant in industrial control due to their ruggedness, reliability, and ability to handle high power levels without semiconductor components. Their operation relies on the nonlinear B-H curve of saturable reactors, enabling amplification through controlled saturation of magnetic cores.

Core Operating Principle

The gain of a magnetic amplifier is governed by the saturation characteristics of its ferromagnetic core. The control winding (input) and load winding (output) share a common magnetic path. When the control current drives the core into saturation, the impedance of the load winding drops sharply, allowing larger currents to flow.

$$ G = \frac{N_c}{N_l} \cdot \frac{\mu_{sat}}{\mu_{unsat}} $$

where G is the gain, Nc and Nl are turns of control and load windings, and μsat, μunsat are permeabilities in saturated/unsaturated states.

Feedback Stabilization

Industrial magamps often employ self-saturating circuits with rectifier feedback to improve response time and linearity. A typical configuration uses:

Core Load

Modern Applications

While largely replaced by solid-state devices, magamps persist in:

Case Study: Steel Mill Current Regulation

A 1980s-era rolling mill employed a 3-stage magamp system to regulate 1500A DC motor currents. The design achieved ±0.5% stability through:

$$ \tau = \frac{L_{core}}{R_{load}} \leq 10ms $$

where τ is the time constant, Lcore is unsaturated inductance, and Rload is motor resistance.

Advantages Over Semiconductor Drives

Parameter Magnetic Amplifier Thyristor Drive
Overload Capacity 500% for 1s 150% for 1s
MTBF >100,000 hrs 50,000 hrs
EMI Susceptibility Immune Requires filtering
Magnetic Amplifier Core Structure Schematic of a magnetic amplifier core showing ferromagnetic core with control and load windings, illustrating saturation effects on impedance. Control Input Control Return Load Output Load Return N_c (Control Turns) N_l (Load Turns) μ_sat μ_unsat Impedance: High (unsat) → Low (sat)
Diagram Description: The diagram would physically show the magnetic core with control and load windings, their spatial arrangement, and the saturation effect on impedance.

3.2 Power Regulation and Conversion

Magnetic amplifiers excel in power regulation due to their inherent nonlinear saturation characteristics. The core's hysteresis loop enables precise control of output power by modulating the DC bias current in the control winding. The relationship between input and output power is governed by the amplifier's gain, which depends on the core material's permeability and the winding configuration.

Core Saturation Dynamics

The power transfer efficiency of a magnetic amplifier is maximized when the core operates near saturation. The critical parameter is the saturation flux density (Bsat), which determines the maximum power handling capability. The output voltage regulation follows:

$$ V_{out} = \frac{N_{load}}{N_{control}} \cdot \frac{d\Phi}{dt} $$

where Nload and Ncontrol are the turns ratios, and dΦ/dt is the rate of change of magnetic flux. The flux density B relates to the applied magnetic field H through the material's hysteresis curve.

Feedback Control for Regulation

Closed-loop regulation is achieved by sampling the output voltage and feeding it back to the control winding. A proportional-integral (PI) controller adjusts the DC bias to maintain stable output under load variations. The transfer function of the regulated system is:

$$ G(s) = \frac{K_p \left(1 + \frac{1}{T_i s}\right)}{1 + \tau s} $$

where Kp is the proportional gain, Ti the integral time constant, and τ the core's effective time delay.

Practical Implementation

In three-phase power systems, magnetic amplifiers are often configured in a delta arrangement to handle higher currents. The following diagram illustrates a typical three-phase magnetic amplifier regulator:

Key design considerations include:

Comparison with Semiconductor Alternatives

While modern switching regulators offer higher efficiency, magnetic amplifiers remain preferred in:

The table below quantifies key performance metrics:

Parameter Magnetic Amplifier Switching Regulator
Efficiency 85-92% 93-98%
Transient Response 10-100 ms 1-10 μs
MTBF >500,000 hrs 100,000 hrs
Three-Phase Magnetic Amplifier Regulator Schematic diagram of a three-phase magnetic amplifier regulator showing delta-connected cores with control and load windings, feedback loop, and saturation dynamics. Phase A Phase B Phase C N_load N_control N_load N_control N_load N_control B_sat B_sat B_sat dΦ/dt dΦ/dt dΦ/dt PI Controller LC Filter
Diagram Description: The section describes a three-phase magnetic amplifier regulator configuration and core saturation dynamics, which are spatial concepts best shown visually.

3.2 Power Regulation and Conversion

Magnetic amplifiers excel in power regulation due to their inherent nonlinear saturation characteristics. The core's hysteresis loop enables precise control of output power by modulating the DC bias current in the control winding. The relationship between input and output power is governed by the amplifier's gain, which depends on the core material's permeability and the winding configuration.

Core Saturation Dynamics

The power transfer efficiency of a magnetic amplifier is maximized when the core operates near saturation. The critical parameter is the saturation flux density (Bsat), which determines the maximum power handling capability. The output voltage regulation follows:

$$ V_{out} = \frac{N_{load}}{N_{control}} \cdot \frac{d\Phi}{dt} $$

where Nload and Ncontrol are the turns ratios, and dΦ/dt is the rate of change of magnetic flux. The flux density B relates to the applied magnetic field H through the material's hysteresis curve.

Feedback Control for Regulation

Closed-loop regulation is achieved by sampling the output voltage and feeding it back to the control winding. A proportional-integral (PI) controller adjusts the DC bias to maintain stable output under load variations. The transfer function of the regulated system is:

$$ G(s) = \frac{K_p \left(1 + \frac{1}{T_i s}\right)}{1 + \tau s} $$

where Kp is the proportional gain, Ti the integral time constant, and τ the core's effective time delay.

Practical Implementation

In three-phase power systems, magnetic amplifiers are often configured in a delta arrangement to handle higher currents. The following diagram illustrates a typical three-phase magnetic amplifier regulator:

Key design considerations include:

Comparison with Semiconductor Alternatives

While modern switching regulators offer higher efficiency, magnetic amplifiers remain preferred in:

The table below quantifies key performance metrics:

Parameter Magnetic Amplifier Switching Regulator
Efficiency 85-92% 93-98%
Transient Response 10-100 ms 1-10 μs
MTBF >500,000 hrs 100,000 hrs
Three-Phase Magnetic Amplifier Regulator Schematic diagram of a three-phase magnetic amplifier regulator showing delta-connected cores with control and load windings, feedback loop, and saturation dynamics. Phase A Phase B Phase C N_load N_control N_load N_control N_load N_control B_sat B_sat B_sat dΦ/dt dΦ/dt dΦ/dt PI Controller LC Filter
Diagram Description: The section describes a three-phase magnetic amplifier regulator configuration and core saturation dynamics, which are spatial concepts best shown visually.

3.3 Military and Aerospace Uses

Reliability in Harsh Environments

Magnetic amplifiers (magamps) are favored in military and aerospace applications due to their inherent ruggedness and immunity to extreme conditions. Unlike semiconductor-based amplifiers, magamps exhibit no performance degradation under high radiation, extreme temperatures, or electromagnetic interference (EMI). Their core saturation principle ensures stable operation even in the presence of ionizing radiation, making them indispensable in satellite and spacecraft power systems.

Power Regulation in Defense Systems

In military radar and communication systems, magamps serve as high-power regulators due to their ability to handle kilowatt-level signals without semiconductor switching losses. The absence of solid-state components eliminates thermal runaway risks in high-duty-cycle applications. For instance, the AN/SPY-1 radar system employs magamps for stable power delivery in phased-array antennas, where precise amplitude control is critical.

$$ \frac{dB}{dt} = \mu_0 \mu_r \frac{N}{l_c} \frac{dH}{dt} $$

Here, B is magnetic flux density, H is magnetic field strength, and lc is core path length. This equation governs the dynamic response of saturable reactors in magamps, enabling precise control of power delivery.

Aerospace Voltage Stabilization

Magamps stabilize bus voltages in aircraft and spacecraft by compensating for load variations without introducing switching noise. The Boeing 787 Dreamliner’s auxiliary power unit (APU) uses magamps to condition 270V DC power, leveraging their fault tolerance—a single magamp failure doesn’t cascade into system-wide collapse, unlike MOSFET-based converters.

Nuclear and EMP Hardening

Strategic defense systems prioritize magamps for electromagnetic pulse (EMP) hardening. When exposed to EMPs, semiconductor devices experience latch-up or gate oxide rupture, whereas magamps remain operational. The U.S. Minuteman III ICBM guidance system historically used magamps in its analog flight computers for this reason, achieving nanosecond-scale response times without vulnerability to transient radiation effects.

Case Study: Satellite Attitude Control

NASA’s Voyager probes utilized magamps in their thruster control systems. The non-linear gain characteristic:

$$ G = \frac{V_{out}}{V_{in}} = \frac{N_s}{N_c} \cdot \frac{1}{1 + \frac{R_{load}}{j\omega L_{sat}}} $$

where Ns and Nc are secondary and control winding turns, allowed precise torque adjustment via magnetic bias currents, eliminating the need for failure-prone mechanical potentiometers in deep-space conditions.

3.3 Military and Aerospace Uses

Reliability in Harsh Environments

Magnetic amplifiers (magamps) are favored in military and aerospace applications due to their inherent ruggedness and immunity to extreme conditions. Unlike semiconductor-based amplifiers, magamps exhibit no performance degradation under high radiation, extreme temperatures, or electromagnetic interference (EMI). Their core saturation principle ensures stable operation even in the presence of ionizing radiation, making them indispensable in satellite and spacecraft power systems.

Power Regulation in Defense Systems

In military radar and communication systems, magamps serve as high-power regulators due to their ability to handle kilowatt-level signals without semiconductor switching losses. The absence of solid-state components eliminates thermal runaway risks in high-duty-cycle applications. For instance, the AN/SPY-1 radar system employs magamps for stable power delivery in phased-array antennas, where precise amplitude control is critical.

$$ \frac{dB}{dt} = \mu_0 \mu_r \frac{N}{l_c} \frac{dH}{dt} $$

Here, B is magnetic flux density, H is magnetic field strength, and lc is core path length. This equation governs the dynamic response of saturable reactors in magamps, enabling precise control of power delivery.

Aerospace Voltage Stabilization

Magamps stabilize bus voltages in aircraft and spacecraft by compensating for load variations without introducing switching noise. The Boeing 787 Dreamliner’s auxiliary power unit (APU) uses magamps to condition 270V DC power, leveraging their fault tolerance—a single magamp failure doesn’t cascade into system-wide collapse, unlike MOSFET-based converters.

Nuclear and EMP Hardening

Strategic defense systems prioritize magamps for electromagnetic pulse (EMP) hardening. When exposed to EMPs, semiconductor devices experience latch-up or gate oxide rupture, whereas magamps remain operational. The U.S. Minuteman III ICBM guidance system historically used magamps in its analog flight computers for this reason, achieving nanosecond-scale response times without vulnerability to transient radiation effects.

Case Study: Satellite Attitude Control

NASA’s Voyager probes utilized magamps in their thruster control systems. The non-linear gain characteristic:

$$ G = \frac{V_{out}}{V_{in}} = \frac{N_s}{N_c} \cdot \frac{1}{1 + \frac{R_{load}}{j\omega L_{sat}}} $$

where Ns and Nc are secondary and control winding turns, allowed precise torque adjustment via magnetic bias currents, eliminating the need for failure-prone mechanical potentiometers in deep-space conditions.

4. Reliability and Durability

4.1 Reliability and Durability

Core Mechanisms Influencing Reliability

Magnetic amplifiers rely on the nonlinear magnetic properties of saturable cores, typically made of grain-oriented silicon steel or nickel-iron alloys. The primary failure modes stem from core hysteresis losses, winding insulation breakdown, and thermal degradation. The reliability is quantified by the mean time between failures (MTBF), which can be derived from the Arrhenius equation for thermal aging:

$$ \text{MTBF} = A e^{\frac{E_a}{kT}} $$

where A is a material-specific constant, Ea is the activation energy, k is Boltzmann’s constant, and T is the absolute temperature.

Thermal Management and Derating

Excessive heat accelerates insulation aging and core losses. The permissible temperature rise (ΔT) is governed by the thermal resistance (Rth) of the magnetic amplifier assembly:

$$ \Delta T = P_{\text{loss}} \cdot R_{\text{th}} $$

where Ploss includes eddy current and hysteresis losses. Derating curves, typically provided by manufacturers, specify the allowable load current reduction at elevated ambient temperatures.

Mechanical Stress and Vibration Resistance

In aerospace and industrial applications, mechanical vibration can lead to winding fatigue or core delamination. The natural frequency (fn) of the assembly must avoid resonance with external vibrations:

$$ f_n = \frac{1}{2\pi} \sqrt{\frac{k}{m}} $$

where k is the stiffness of the mounting structure and m is the mass of the core and windings. Damping materials like silicone potting compounds are often used to mitigate high-frequency oscillations.

Case Study: Military-Grade Magnetic Amplifiers

U.S. military specifications (e.g., MIL-STD-810) require magnetic amplifiers to endure:

Data from field deployments show that properly potted units achieve MTBF values exceeding 100,000 hours under these conditions.

Material Selection for Longevity

The choice of core material directly impacts durability:

Accelerated Life Testing (ALT)

ALT protocols apply elevated stress levels (temperature, voltage, vibration) to predict failure rates. The Eyring model is commonly used for combined thermal-electrical stresses:

$$ L = \frac{1}{V^m e^{\frac{B}{T}}} $$

where L is the lifetime, V is the applied voltage, T is temperature, and m, B are empirical constants.

4.1 Reliability and Durability

Core Mechanisms Influencing Reliability

Magnetic amplifiers rely on the nonlinear magnetic properties of saturable cores, typically made of grain-oriented silicon steel or nickel-iron alloys. The primary failure modes stem from core hysteresis losses, winding insulation breakdown, and thermal degradation. The reliability is quantified by the mean time between failures (MTBF), which can be derived from the Arrhenius equation for thermal aging:

$$ \text{MTBF} = A e^{\frac{E_a}{kT}} $$

where A is a material-specific constant, Ea is the activation energy, k is Boltzmann’s constant, and T is the absolute temperature.

Thermal Management and Derating

Excessive heat accelerates insulation aging and core losses. The permissible temperature rise (ΔT) is governed by the thermal resistance (Rth) of the magnetic amplifier assembly:

$$ \Delta T = P_{\text{loss}} \cdot R_{\text{th}} $$

where Ploss includes eddy current and hysteresis losses. Derating curves, typically provided by manufacturers, specify the allowable load current reduction at elevated ambient temperatures.

Mechanical Stress and Vibration Resistance

In aerospace and industrial applications, mechanical vibration can lead to winding fatigue or core delamination. The natural frequency (fn) of the assembly must avoid resonance with external vibrations:

$$ f_n = \frac{1}{2\pi} \sqrt{\frac{k}{m}} $$

where k is the stiffness of the mounting structure and m is the mass of the core and windings. Damping materials like silicone potting compounds are often used to mitigate high-frequency oscillations.

Case Study: Military-Grade Magnetic Amplifiers

U.S. military specifications (e.g., MIL-STD-810) require magnetic amplifiers to endure:

Data from field deployments show that properly potted units achieve MTBF values exceeding 100,000 hours under these conditions.

Material Selection for Longevity

The choice of core material directly impacts durability:

Accelerated Life Testing (ALT)

ALT protocols apply elevated stress levels (temperature, voltage, vibration) to predict failure rates. The Eyring model is commonly used for combined thermal-electrical stresses:

$$ L = \frac{1}{V^m e^{\frac{B}{T}}} $$

where L is the lifetime, V is the applied voltage, T is temperature, and m, B are empirical constants.

4.2 Efficiency and Performance Trade-offs

The efficiency of a magnetic amplifier is fundamentally governed by core losses, winding resistance, and control circuit dynamics. Unlike semiconductor amplifiers, where switching losses dominate, magnetic amplifiers exhibit hysteresis and eddy current losses that scale nonlinearly with frequency and flux density. The total power dissipation Ploss can be decomposed into:

$$ P_{loss} = P_{hysteresis} + P_{eddy} + P_{copper} $$

Core Losses and Hysteresis Trade-offs

Hysteresis loss, derived from the area of the B-H loop, follows Steinmetz's empirical relation:

$$ P_h = k_h f B_m^n $$

where kh is the material constant, f is frequency, Bm is peak flux density, and n (typically 1.6–2.1) depends on core material. High-permeability cores like nanocrystalline alloys reduce kh but may saturate at lower control currents, limiting gain.

Eddy Current Losses and Frequency Dependence

Eddy currents, induced by time-varying flux, are minimized by laminating the core or using powdered materials. The loss is approximated by:

$$ P_e = k_e f^2 B_m^2 t^2 / \rho $$

Here, t is lamination thickness and ρ is resistivity. For high-frequency designs (e.g., >10 kHz), ferrite cores become essential despite their lower saturation flux density.

Copper Losses and Winding Optimization

Resistive losses in windings follow Pcopper = I2Rac, where Rac accounts for skin and proximity effects. Litz wire or foil windings mitigate this at high frequencies, but increase parasitic capacitance, introducing a trade-off between efficiency and bandwidth.

Efficiency vs. Linearity

Magnetic amplifiers achieve high efficiency (>90%) in saturation mode, but linear operation (for low-distortion applications) forces operation below saturation, increasing core losses. The linearity-efficiency product η·THD is a key figure of merit, often optimized via feedback control or pre-biasing techniques.

Thermal Management Implications

Core losses manifest as heat, requiring derating above 80–100°C. Forced air cooling or liquid cooling may be necessary in high-power designs (>1 kW), adding volume and cost. Thermal resistance models must account for core-winding thermal coupling, as hotspots degrade insulation over time.

B (Flux Density) H (Field Intensity)

Practical designs balance these factors through iterative simulation and material selection, often leveraging finite-element analysis (FEA) tools for loss modeling. Military and aerospace applications, where reliability trumps efficiency, may prioritize derated operation, while industrial drives push efficiency boundaries with advanced core materials like Metglas.

B-H Hysteresis Loop and Loss Components A B-H hysteresis loop showing flux density (B) versus magnetic field intensity (H), with annotations for saturation points, coercivity, and hysteresis loss area. B (T) H (A/m) Initial Saturation H_c B_m P_h Hysteresis Loss
Diagram Description: The section discusses B-H loops and core losses, which are inherently visual concepts requiring spatial representation of hysteresis curves and flux density relationships.

4.2 Efficiency and Performance Trade-offs

The efficiency of a magnetic amplifier is fundamentally governed by core losses, winding resistance, and control circuit dynamics. Unlike semiconductor amplifiers, where switching losses dominate, magnetic amplifiers exhibit hysteresis and eddy current losses that scale nonlinearly with frequency and flux density. The total power dissipation Ploss can be decomposed into:

$$ P_{loss} = P_{hysteresis} + P_{eddy} + P_{copper} $$

Core Losses and Hysteresis Trade-offs

Hysteresis loss, derived from the area of the B-H loop, follows Steinmetz's empirical relation:

$$ P_h = k_h f B_m^n $$

where kh is the material constant, f is frequency, Bm is peak flux density, and n (typically 1.6–2.1) depends on core material. High-permeability cores like nanocrystalline alloys reduce kh but may saturate at lower control currents, limiting gain.

Eddy Current Losses and Frequency Dependence

Eddy currents, induced by time-varying flux, are minimized by laminating the core or using powdered materials. The loss is approximated by:

$$ P_e = k_e f^2 B_m^2 t^2 / \rho $$

Here, t is lamination thickness and ρ is resistivity. For high-frequency designs (e.g., >10 kHz), ferrite cores become essential despite their lower saturation flux density.

Copper Losses and Winding Optimization

Resistive losses in windings follow Pcopper = I2Rac, where Rac accounts for skin and proximity effects. Litz wire or foil windings mitigate this at high frequencies, but increase parasitic capacitance, introducing a trade-off between efficiency and bandwidth.

Efficiency vs. Linearity

Magnetic amplifiers achieve high efficiency (>90%) in saturation mode, but linear operation (for low-distortion applications) forces operation below saturation, increasing core losses. The linearity-efficiency product η·THD is a key figure of merit, often optimized via feedback control or pre-biasing techniques.

Thermal Management Implications

Core losses manifest as heat, requiring derating above 80–100°C. Forced air cooling or liquid cooling may be necessary in high-power designs (>1 kW), adding volume and cost. Thermal resistance models must account for core-winding thermal coupling, as hotspots degrade insulation over time.

B (Flux Density) H (Field Intensity)

Practical designs balance these factors through iterative simulation and material selection, often leveraging finite-element analysis (FEA) tools for loss modeling. Military and aerospace applications, where reliability trumps efficiency, may prioritize derated operation, while industrial drives push efficiency boundaries with advanced core materials like Metglas.

B-H Hysteresis Loop and Loss Components A B-H hysteresis loop showing flux density (B) versus magnetic field intensity (H), with annotations for saturation points, coercivity, and hysteresis loss area. B (T) H (A/m) Initial Saturation H_c B_m P_h Hysteresis Loss
Diagram Description: The section discusses B-H loops and core losses, which are inherently visual concepts requiring spatial representation of hysteresis curves and flux density relationships.

4.3 Modern Alternatives and Obsolescence

Magnetic amplifiers, once prominent in early-to-mid 20th-century power control and signal processing, have largely been supplanted by semiconductor-based alternatives. The transition was driven by semiconductor devices offering superior efficiency, faster response times, and compact form factors. The primary competitors include silicon-controlled rectifiers (SCRs), insulated-gate bipolar transistors (IGBTs), and power MOSFETs.

Semiconductor-Based Replacements

The displacement of magnetic amplifiers by solid-state devices can be attributed to several key advantages:

The gain of a semiconductor amplifier, such as a MOSFET, is governed by its transconductance (gm):

$$ g_m = \frac{\partial I_D}{\partial V_{GS}} $$

where ID is the drain current and VGS is the gate-source voltage. This parameter is orders of magnitude higher than the effective gain achievable in magnetic amplifiers.

Niche Applications of Magnetic Amplifiers

Despite obsolescence in mainstream electronics, magnetic amplifiers persist in specialized scenarios:

Comparative Analysis: Magnetic vs. Solid-State Amplifiers

The following table summarizes key differences:

Parameter Magnetic Amplifier Solid-State Amplifier
Bandwidth ~kHz ~MHz-GHz
Efficiency 70-85% 90-98%
Size/Weight Bulky Compact
Failure Mode Graceful degradation Catastrophic

Future Prospects

Research into advanced magnetic materials, such as metallic glasses and nanocrystalline cores, aims to revive interest in magnetic amplifiers for ultra-high-reliability applications. However, the dominance of semiconductor technology in power electronics remains unchallenged due to continuous advancements in wide-bandgap materials like silicon carbide (SiC) and gallium nitride (GaN).

$$ R_{on} = \frac{V_{DS}}{I_D} $$

where Ron represents the on-resistance of a power MOSFET, a critical factor in minimizing conduction losses. Modern SiC devices achieve Ron values below 10 mΩ, further marginalizing magnetic solutions.

4.3 Modern Alternatives and Obsolescence

Magnetic amplifiers, once prominent in early-to-mid 20th-century power control and signal processing, have largely been supplanted by semiconductor-based alternatives. The transition was driven by semiconductor devices offering superior efficiency, faster response times, and compact form factors. The primary competitors include silicon-controlled rectifiers (SCRs), insulated-gate bipolar transistors (IGBTs), and power MOSFETs.

Semiconductor-Based Replacements

The displacement of magnetic amplifiers by solid-state devices can be attributed to several key advantages:

The gain of a semiconductor amplifier, such as a MOSFET, is governed by its transconductance (gm):

$$ g_m = \frac{\partial I_D}{\partial V_{GS}} $$

where ID is the drain current and VGS is the gate-source voltage. This parameter is orders of magnitude higher than the effective gain achievable in magnetic amplifiers.

Niche Applications of Magnetic Amplifiers

Despite obsolescence in mainstream electronics, magnetic amplifiers persist in specialized scenarios:

Comparative Analysis: Magnetic vs. Solid-State Amplifiers

The following table summarizes key differences:

Parameter Magnetic Amplifier Solid-State Amplifier
Bandwidth ~kHz ~MHz-GHz
Efficiency 70-85% 90-98%
Size/Weight Bulky Compact
Failure Mode Graceful degradation Catastrophic

Future Prospects

Research into advanced magnetic materials, such as metallic glasses and nanocrystalline cores, aims to revive interest in magnetic amplifiers for ultra-high-reliability applications. However, the dominance of semiconductor technology in power electronics remains unchallenged due to continuous advancements in wide-bandgap materials like silicon carbide (SiC) and gallium nitride (GaN).

$$ R_{on} = \frac{V_{DS}}{I_D} $$

where Ron represents the on-resistance of a power MOSFET, a critical factor in minimizing conduction losses. Modern SiC devices achieve Ron values below 10 mΩ, further marginalizing magnetic solutions.

5. Key Research Papers

5.1 Key Research Papers

5.1 Key Research Papers

5.2 Recommended Books

5.3 Online Resources