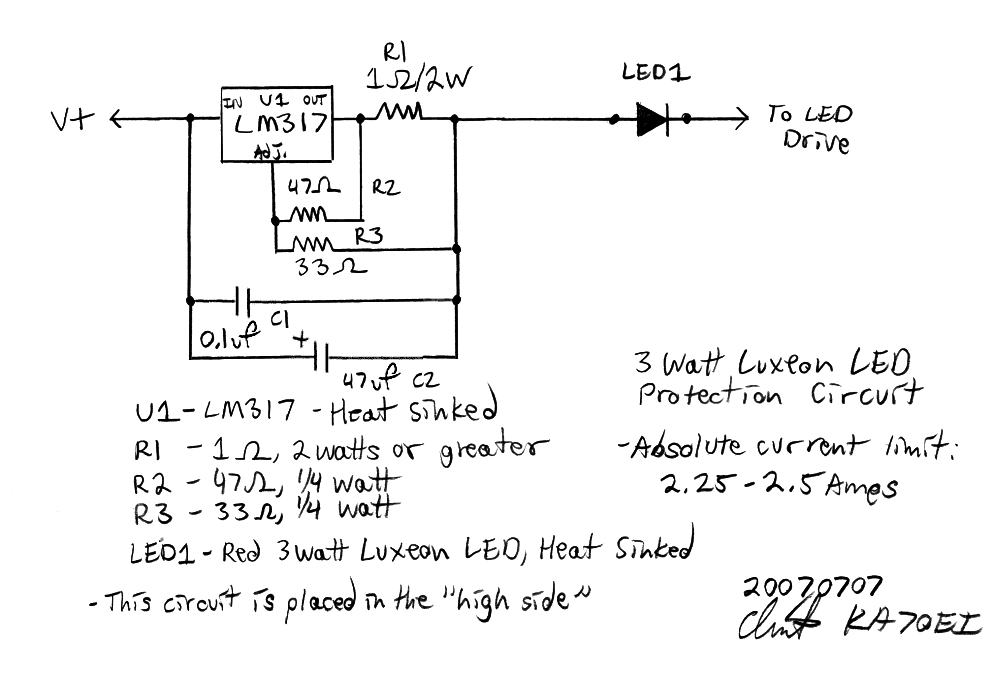
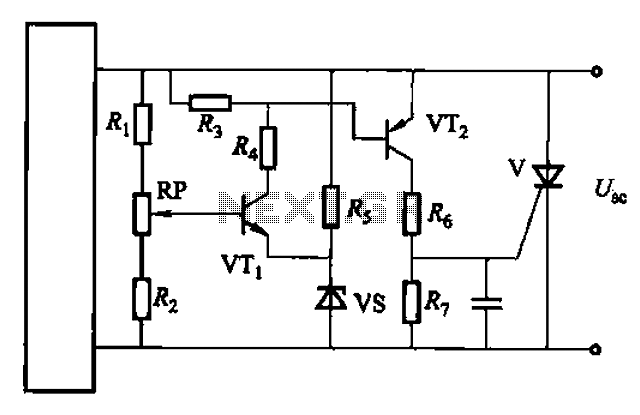
Overcurrent Protection Circuits
1. Definition and Importance of Overcurrent Protection
Definition and Importance of Overcurrent Protection
Overcurrent protection refers to the implementation of safeguards in electrical and electronic systems to prevent damage caused by currents exceeding the designed operational limits. In practical terms, this involves interrupting or limiting the current flow when it surpasses a predetermined threshold, thereby preserving the integrity of components, wiring, and connected devices.
Fundamental Principles
The underlying physics of overcurrent phenomena can be analyzed through Joule heating and conductor limitations. When current I flows through a conductor with resistance R, the power dissipated as heat is given by:
This quadratic relationship means that small increases in current can lead to significant temperature rises. For example, a 50% overcurrent condition results in 125% additional heat dissipation, potentially exceeding material thermal limits.
Critical Protection Parameters
Effective overcurrent protection requires consideration of three key parameters:
- Threshold current: The precise value at which protection activates
- Response time: The delay between fault detection and protective action
- Interruption capacity: The maximum fault current the protection can safely interrupt
These parameters must be carefully matched to the protected system's characteristics. For instance, semiconductor devices typically require faster protection (microsecond response) compared to electromechanical systems (millisecond response).
Practical Implementation Challenges
Modern electronics present unique challenges for overcurrent protection due to:
- Increasing power densities in miniaturized systems
- Higher switching frequencies in power electronics
- Complex fault current distributions in multi-phase systems
In power distribution networks, fault currents can reach hundreds of kiloamperes, necessitating protection devices with both rapid response and massive interruption capacity. The coordination of protection across multiple system levels creates additional engineering complexity.
Historical Context and Evolution
The development of overcurrent protection parallels the growth of electrical systems. Early electromechanical circuit breakers in the 19th century gave way to solid-state designs in the 1960s, enabling faster response times. Modern protection schemes increasingly incorporate digital monitoring and predictive algorithms to anticipate rather than react to faults.
System-Level Considerations
Effective protection requires analysis of the complete system impedance characteristics. The prospective short-circuit current at any point can be calculated from:
where Ztotal represents the sum of source impedance, line impedance, and fault impedance. Protection devices must be rated for the maximum possible Isc at their installation point.
1.2 Common Causes of Overcurrent
Short Circuits
Short circuits occur when a low-resistance path bypasses the intended load, causing current to surge beyond safe limits. This typically arises from insulation breakdown, component failure, or accidental bridging of conductors. The resulting current Isc can be derived from Ohm's Law:
where Rfault approaches zero, leading to theoretically infinite current. Practical limits are imposed by source impedance and conductor resistance.
Inrush Current
Capacitive and inductive loads (e.g., motors, transformers, bulk capacitors) draw high transient currents during startup. For a capacitor charging through resistance R:
This exponential decay can exceed steady-state current by 10–100×, stressing components.
Load Faults
Overcurrent manifests when:
- Load impedance drops unexpectedly (e.g., motor stalling, partial short circuits)
- Regenerative energy feedback in motor drives or inductive loads
- Component degradation increasing leakage currents (e.g., electrolytic capacitor ESR rise)
Design and Operational Errors
Common engineering oversights include:
- Inadequate wire gauge selection relative to peak current
- Improper fuse or circuit breaker ratings
- Parasitic oscillations in switching converters causing current ringing
Environmental Factors
External conditions exacerbate overcurrent risks:
- Temperature extremes altering semiconductor junction properties
- Voltage transients (e.g., lightning, ESD) triggering latch-up in ICs
- Contamination creating leakage paths on PCBs
Case Study: MOSFET Failure
A common failure mode occurs when a power MOSFET's drain-source resistance (RDS(on)) becomes nonlinear at high currents, leading to thermal runaway. The power dissipation follows:
where Tj is junction temperature. Positive feedback between RDS(on) and temperature can destroy the device within microseconds.
1.3 Consequences of Overcurrent in Circuits
Thermal Damage and Joule Heating
When current exceeds a component's rated capacity, resistive heating follows Joule's law:
where P is power dissipation, I is overcurrent, and R is the conductor resistance. This quadratic relationship means a 2× overcurrent produces 4× the heat. In integrated circuits, localized heating can create thermal gradients exceeding 106 °C/m, leading to:
- Metal trace electromigration (atomic displacement at current densities >105 A/cm2)
- Dielectric breakdown in semiconductors
- PCB delamination above glass transition temperatures (typically 130-180°C)
Voltage Regulation Failure
Overcurrent forces voltage regulators into dropout or current limiting modes. For an LDO regulator with dropout voltage VDO and load current IL:
where RDS(on) is the pass transistor's on-resistance. Sustained overcurrent causes:
- Output voltage collapse (often triggering brownout resets)
- Increased ripple voltage (ΔV ≈ IRMS/(2πfC))
- Phase margin degradation in switching converters
Arc Formation and Insulation Breakdown
At sufficient voltages (>12V DC or 30V AC), overcurrent can ionize air or dielectric materials. The Paschen curve describes breakdown voltage Vb as:
where p is pressure, d is gap distance, and γse is the secondary electron emission coefficient. Consequences include:
- Carbon tracking on PCB surfaces (irreversible conductivity paths)
- Plasma formation in relays/connectors (contact erosion rates >1μm/operation)
- Partial discharge in transformers (cumulative insulation damage)
Electromagnetic Interference (EMI)
Fast overcurrent transients (di/dt > 1A/ns) generate broadband EMI through:
This manifests as:
- Radiated emissions exceeding FCC Part 15 limits (3m measurements >40dBμV/m)
- Ground bounce (ΔV = Lloop di/dt, where Lloop ≈ 20nH/cm)
- Crosstalk in adjacent traces (capacitive coupling ∝ fedgeVnoise)
Catastrophic Failure Modes
Extreme overcurrent (>10× rating) induces failure mechanisms with distinct time constants:
| Component | Failure Mode | Time Constant |
|---|---|---|
| Silicon diodes | Thermal runaway | 10μs-1ms |
| MLCC capacitors | Microcracking | 1-100μs |
| PCB traces | Fusing | 1-100ms |
Copper traces fuse at current densities following the Onderdonk equation:
where A is cross-sectional area (mils2), K=0.024 for internal layers, and Tm is melting temperature (1083°C for Cu).
2. Fuses: Operation and Selection Criteria
2.1 Fuses: Operation and Selection Criteria
Fundamental Operation of Fuses
A fuse is a passive overcurrent protection device designed to interrupt a circuit by melting its fusible element when the current exceeds a predetermined threshold. The operation relies on Joule heating, where the power dissipated in the fuse element raises its temperature until it reaches the melting point. The time-current characteristic follows the integral of energy dissipation:
Here, I is the current, t is the time to melt, and k is a constant determined by the fuse material and geometry. This relationship implies that fuses respond to the thermal energy accumulation rather than instantaneous current.
Key Parameters for Fuse Selection
Selecting an appropriate fuse requires evaluating multiple interdependent parameters:
- Rated Current (In) – The maximum continuous current the fuse can carry without opening. Typically derated by 25% for reliability.
- Breaking Capacity (Imax) – The maximum fault current the fuse can safely interrupt without arcing or fragmentation.
- Voltage Rating – Must exceed the system's maximum operating voltage to prevent dielectric breakdown after melting.
- Time-Current Curve – Defines the melting time as a function of overcurrent magnitude. Critical for coordination with other protective devices.
- I2t Value – The energy required to melt the element, crucial for protecting semiconductor devices with limited thermal mass.
Fuse Types and Applications
Cartridge Fuses
Enclosed in ceramic or glass bodies with metal end caps. High-breaking-capacity (HBC) versions use granular quartz filler to quench arcs. Common in industrial power distribution up to 600V AC.
Semiconductor Fuses
Designed with ultra-fast melting elements (silver or copper with M-effect spots) to protect IGBTs and thyristors. Characterized by very low I2t values (e.g., 50 A2s for a 100A fuse).
Surface-Mount Fuses
Constructed using thin-film metallization on ceramic substrates. Used in compact electronics where PCB space is constrained. Typical ratings range from 50mA to 5A.
Derating Considerations
Fuse performance degrades under:
- Ambient Temperature – Most fuses derate linearly above 25°C. For example, a fuse rated 10A at 25°C may carry only 7A at 65°C.
- Pulse Conditions – Repetitive current pulses cause cumulative damage to the element. Manufacturers provide pulse durability curves (e.g., 100,000 pulses at 50% In).
- Enclosure Effects – Poor ventilation increases thermal resistance, requiring further derating.
Coordination with Other Protective Devices
When fuses coexist with circuit breakers or relays, their time-current curves must be analyzed to ensure selective tripping. The fuse should clear faults faster than downstream devices for localized protection. The coordination margin follows:
Modern design tools like ETAP or SKM Power*Tools automate this analysis by simulating fault scenarios across the protection hierarchy.
2.2 Circuit Breakers: Types and Applications
Fundamental Operating Principles
Circuit breakers function as automatic switches designed to interrupt current flow upon detecting an overcurrent condition. The interruption mechanism relies on electromechanical or solid-state principles, depending on the breaker type. The tripping current threshold Itrip is determined by:
where k is a multiplier (typically 1.25–10) and Irated is the breaker's nominal current rating. The time-current characteristic follows an inverse relationship, described by:
where K and n are constants specific to the breaker's trip curve (e.g., B, C, D curves in IEC standards).
Major Breaker Types
Thermal-Magnetic Breakers
These combine a bimetallic strip (thermal) for overload protection and an electromagnetic coil (magnetic) for short-circuit protection. The thermal element responds to I²t heating with typical trip times of 2–20 seconds for moderate overloads, while the magnetic element operates in milliseconds for high-current faults.
Electronic Trip Units
Modern molded-case circuit breakers (MCCBs) often incorporate microprocessor-based trip units with programmable settings. These allow precise adjustment of:
- Long-time pickup (Ir)
- Short-time pickup (Isd)
- Instantaneous pickup (Ii)
- Ground-fault pickup (Ig)
The trip algorithm typically implements:
where α and β are curve shaping exponents (typically 0.5–2).
Hybrid DC Breakers
For high-voltage DC applications (e.g., HVDC transmission, EV charging), hybrid breakers combine mechanical contacts with parallel IGBT or thyristor paths. The commutation process during interruption follows:
where L is the loop inductance, C is the snubber capacitance, and Varc is the arc voltage.
Application-Specific Designs
Miniature Circuit Breakers (MCBs)
Common in residential and commercial installations, MCBs feature standardized trip curves:
- Type B: 3–5×In (general purpose)
- Type C: 5–10×In (motor circuits)
- Type D: 10–20×In (transformer inrush)
Air Circuit Breakers (ACBs)
Used in industrial power distribution (400–6300A), ACBs employ arc chutes with splitter plates to stretch and cool the arc. The interrupting capacity follows:
where Zsys is the system impedance at the fault point.
Vacuum Circuit Breakers
Common in medium-voltage applications (1–38kV), vacuum interrupters extinguish arcs through rapid dielectric recovery. The critical post-arc current density is given by:
where Vrec is the recovery voltage, d is the contact gap, and τ is the plasma decay time constant.
Selection Criteria
When specifying circuit breakers, engineers must evaluate:
- Voltage rating (Ue)
- Current rating (In)
- Breaking capacity (Icu)
- Trip curve characteristics
- Environmental conditions (altitude, temperature)
- Selective coordination requirements
The coordination time interval (CTI) between upstream and downstream breakers is typically 0.1–0.3 seconds, determined by:
where tmargin accounts for manufacturing tolerances (usually 50–100ms).
2.3 Electronic Overcurrent Protection Circuits
Electronic overcurrent protection circuits leverage active semiconductor components to detect and interrupt excessive current flow with high precision and speed. Unlike passive methods (e.g., fuses or PTC thermistors), these circuits provide adjustable trip thresholds, faster response times, and automatic reset capabilities, making them indispensable in modern power electronics, motor drives, and battery management systems.
Current Sensing Techniques
Accurate current measurement is fundamental to overcurrent protection. Three primary methods dominate:
- Shunt Resistors: A low-value resistor in series with the load generates a voltage drop proportional to current (Ohm’s Law). For high currents (I > 10A), manganin or alloy shunts minimize temperature drift.
- Hall-Effect Sensors: Galvanically isolated measurement via magnetic field detection, suitable for high-voltage or bidirectional current applications.
- Rogowski Coils: Inductive sensors for AC systems, offering linear response without saturation.
Comparator-Based Trip Circuit
A threshold comparator triggers when the sensed voltage exceeds a reference (Vref). The reference can be static (fixed by resistors) or dynamic (controlled by a microcontroller). Hysteresis is critical to prevent chatter:
For example, an LM311 comparator with a 10kΩ/100kΩ feedback network and 5V output swing introduces 0.45V hysteresis, rejecting noise-induced false triggers.
Active Current Limiting with MOSFETs
Linear regulators or power MOSFETs can enforce a hard current limit by operating in the saturation region. The gate drive adjusts dynamically to clamp Iload:
In switch-mode supplies, this approach reduces thermal stress compared to abrupt shutdown. Modern ICs like the LTC4365 integrate MOSFET control with sub-microsecond response.
Foldback Current Limiting
This technique reduces the trip threshold as voltage drops, minimizing power dissipation during faults. The foldback characteristic is defined by:
where n adjusts the slope. Foldback is common in audio amplifiers and DC-DC converters but requires careful stability analysis to avoid latch-up.
Case Study: Solid-State Circuit Breaker
A 48V automotive system might use a bidirectional GaN HEMT with desaturation detection. When VDS exceeds 2V (indicating overcurrent), a gate driver IC (e.g., UCC27531) shuts off the FET in < 100ns. Energy absorption is handled by a transient voltage suppressor (TVS) diode array.
3. Current Sensing Techniques
Current Sensing Techniques
Shunt Resistor-Based Sensing
The most direct method for current sensing involves measuring the voltage drop across a precision shunt resistor placed in series with the load. Ohm's Law governs the relationship:
For high-current applications, low-resistance shunts (typically 0.1 mΩ to 100 mΩ) minimize power dissipation. The voltage signal is amplified using a differential amplifier or instrumentation amplifier. Key considerations include:
- Resistor temperature coefficient (TCR) and power rating
- Kelvin (4-wire) connections to eliminate lead resistance errors
- Common-mode voltage limitations of the amplifier
Magnetic Field-Based Sensing
Non-contact methods exploit Ampere's Law, where current generates a proportional magnetic field. Two primary implementations exist:
Current Transformers (CTs)
CTs provide galvanic isolation and work on AC currents only. The secondary current relates to the primary current by the turns ratio:
Core saturation limits the measurable current range, while frequency response depends on core material (laminated steel for power frequencies, nanocrystalline alloys for wider bandwidth).
Hall Effect Sensors
Hall sensors measure DC and AC currents by detecting the magnetic field perpendicular to current flow. The output voltage is:
where KH is the Hall coefficient. Modern integrated solutions (e.g., Allegro ACS712) combine Hall elements with signal conditioning, offering sensitivities down to 20 mV/A.
Rogowski Coils
These air-core coils measure alternating current by sensing the rate of change of magnetic flux:
where M is the mutual inductance. The output requires integration to recover the current waveform. Advantages include linear response, no saturation effects, and suitability for high-frequency measurements (up to MHz range).
Giant Magnetoresistance (GMR) Sensors
GMR sensors exploit quantum mechanical spin-dependent scattering in thin ferromagnetic layers. They offer:
- Higher sensitivity than Hall effect sensors (ΔR/R up to 20%)
- Bandwidth extending to several MHz
- Directional sensitivity enabling vector current measurement
The resistance change follows:
where RP and RAP are resistances in parallel and antiparallel magnetization states.
Fiber Optic Current Sensors
Based on the Faraday effect, these sensors measure the rotation of polarized light in a magneto-optic material:
where V is the Verdet constant. Used in high-voltage applications (e.g., power grid monitoring) due to complete galvanic isolation and immunity to electromagnetic interference.
Threshold Setting and Hysteresis
Threshold Voltage Determination
The threshold voltage (Vth) in an overcurrent protection circuit defines the current level at which the protection mechanism triggers. For a comparator-based design, Vth is derived from the voltage drop across a current-sensing resistor (Rsense). The relationship is given by:
where Itrip is the desired trip current. To ensure stability against noise, Rsense must be chosen such that Vth is sufficiently above the comparator's input offset voltage.
Hysteresis Implementation
Hysteresis prevents rapid toggling of the protection circuit near the threshold due to noise or transient fluctuations. It is implemented by introducing positive feedback, typically via a resistor (Rhys) between the comparator output and its non-inverting input. The hysteresis window (Vhys) is calculated as:
where R1 and R2 form the feedback divider network, and Vout(max) is the comparator's maximum output voltage. The upper and lower thresholds (Vth+ and Vth-) are then:
Practical Design Considerations
Noise Immunity: A wider hysteresis band improves noise rejection but delays the circuit's response to legitimate overcurrent events. The optimal Vhys balances these trade-offs. For example, in motor control applications, hysteresis is often set to 5–10% of Vth to handle back-EMF transients.
Component Tolerance: Resistor tolerances directly impact threshold accuracy. Using 1% or 0.1% tolerance resistors minimizes deviation from the designed Vth. Temperature coefficients of Rsense and feedback resistors must also be matched to maintain stability across operating conditions.
Case Study: Hysteresis in a Buck Converter
In a 12V-to-5V buck converter with a 10A current limit, Rsense = 5mΩ sets Vth = 50mV. With R1 = 10kΩ, R2 = 100kΩ, and Vout(max) = 3.3V, the hysteresis window is:
This results in a 150mV margin above and below Vth, effectively filtering out high-frequency switching noise.
3.3 Response Time Considerations
Fundamental Trade-offs in Response Time
The response time of an overcurrent protection circuit is governed by the interplay between detection speed and false-trigger immunity. Faster response times reduce thermal stress on protected components but increase susceptibility to transient current spikes. The time constant (τ) of the protection circuit can be derived from first principles:
where Rsense is the current-sensing resistance, Cfilter the noise-filtering capacitance, and Lparasitic the loop inductance. For circuits requiring <1μs response, the second term often dominates due to PCB trace inductance (typically 10-50nH/cm).
Digital vs Analog Implementation
Modern protection circuits use either:
- Analog comparators (50-200ns latency) with hysteresis to prevent chatter
- Digital controllers (1-10μs latency) implementing advanced algorithms like:
where N represents the number of averaging cycles in digital implementations. Field-programmable gate arrays (FPGAs) can achieve <500ns response times through parallel processing of current samples.
Transient Analysis and Di/dt Effects
For inductive loads, the rate of current rise (di/dt) must be considered:
This back-EMF can delay protection triggering. Practical solutions include:
- Active clamping circuits using MOSFETs with <10ns turn-on
- Predictive algorithms in digital controllers
- Multi-stage protection with fast analog triggers and slower digital validation
Case Study: Power Semiconductor Protection
IGBT modules require <2μs protection to prevent thermal runaway. A 2023 study (IEEE Trans. Power Electron.) demonstrated a hybrid approach achieving 750ns response:
The implementation used:
- 50MHz bandwidth current sensor
- Windowed comparator with 5ns propagation delay
- GaN-based crowbar circuit
4. Overcurrent Protection in Power Supplies
4.1 Overcurrent Protection in Power Supplies
Fundamentals of Overcurrent Protection
Overcurrent protection (OCP) in power supplies safeguards against excessive current flow, which can result from short circuits, overloads, or component failures. The primary objective is to interrupt the current path before thermal or electrical stress damages sensitive components. Two dominant mechanisms are employed:
- Current Limiting: Actively restricts current to a predefined threshold.
- Circuit Breaking: Disconnects the load entirely upon fault detection.
Current Sensing Techniques
Accurate current measurement is critical for OCP. Common methods include:
- Shunt Resistors: A low-resistance element (Rshunt) placed in series with the load. The voltage drop (Vshunt = I × Rshunt) is amplified and compared to a reference.
- Hall-Effect Sensors: Non-contact measurement via magnetic field detection, suitable for high-current applications.
Design Considerations for OCP Circuits
The response time (tresponse) of an OCP circuit must balance speed and stability. A fast response prevents damage but may trigger false positives due to transient currents. The trade-off is quantified by:
where fc is the cutoff frequency of the detection circuit, Ithreshold is the OCP trigger current, and Inoise is the peak noise current.
Implementation Example: Foldback Current Limiting
Foldback limiting reduces the current threshold as the load voltage drops, minimizing power dissipation during faults. The current limit (Ilim) follows:
where Imax is the maximum allowable current and Vnom is the nominal output voltage.
Practical Challenges and Mitigations
False triggering due to inrush currents is a common issue. A time-delayed OCP or soft-start circuit can mitigate this. For example, a MOSFET-based soft-start circuit gradually increases the current limit during startup:
Case Study: OCP in Switch-Mode Power Supplies (SMPS)
In SMPS designs, OCP is often integrated into the pulse-width modulation (PWM) controller. For instance, the UC3842 IC uses cycle-by-cycle current limiting via a comparator that monitors the voltage across a sense resistor. The duty cycle is clamped when the sensed current exceeds the threshold:
where Dmax is the maximum duty cycle, Vsense is the sensed voltage, and Vramp is the internal ramp voltage of the PWM controller.
4.2 Protection in Motor Control Circuits
Motor control circuits are particularly susceptible to overcurrent conditions due to high inrush currents during startup, mechanical overloads, or short circuits. Implementing robust overcurrent protection requires an understanding of motor dynamics, fault modes, and circuit response times.
Motor Starting Current and Locked Rotor Conditions
During startup, AC induction motors draw 5–8 times their rated current (locked rotor current) until reaching operating speed. This transient must be accommodated without triggering false protection. The thermal time constant of the motor and protective device must be matched:
where k ranges from 5–8 for standard NEMA design motors. The permissible duration before protection intervenes follows:
tsafe being the motor's thermal withstand time at locked rotor current.
Protection Device Selection Criteria
Effective motor protection requires devices with:
- Inverse-time characteristics to tolerate startup currents
- Instantaneous trip thresholds above inrush but below fault currents
- Coordinated response with motor thermal limits (I2t matching)
For DC motors, the absence of slip necessitates different considerations:
where kt is the torque constant. Stalled conditions lead to rapid current buildup requiring faster protection.
Solid-State Motor Controllers
Modern drives implement multi-stage protection through:
- Current transformers with 1–5ms response time
- IGBT desaturation detection (≤10μs response)
- Software-based I2t algorithms
The protection hierarchy in a typical VFD includes:
Practical Implementation Considerations
When designing motor protection circuits:
- Class 10 (fast) or Class 20 (slow) overload relays must match motor starting characteristics
- Current sensors should have bandwidth exceeding the highest expected di/dt (≥10kHz for PWM drives)
- Ground fault protection requires sensitive detection (5–10% of rated current)
For servo systems, the protection scheme must account for regenerative braking currents:
where Ekinetic represents the rotating energy being returned to the DC bus.
4.3 Overcurrent Protection in Battery Management Systems
Battery Management Systems (BMS) require robust overcurrent protection to prevent catastrophic failures caused by excessive discharge currents, short circuits, or fault conditions. Unlike conventional power systems, lithium-ion batteries exhibit nonlinear thermal runaway characteristics where overcurrent events can lead to irreversible damage within milliseconds.
Current Sensing Techniques
Precision current measurement forms the foundation of BMS overcurrent protection. Three primary methods dominate modern implementations:
- Shunt resistors: Low-value (50-200 μΩ) precision resistors with Kelvin connections provide the most accurate DC measurement, though they introduce power losses.
- Hall-effect sensors: Isolated current measurement without insertion loss, but suffer from temperature drift and DC offset errors.
- Current transformers: Only suitable for AC components in switching circuits, unable to measure DC current.
The voltage drop across a shunt resistor relates to current through Ohm's Law:
Protection Threshold Dynamics
Lithium-ion batteries require multi-tiered protection thresholds based on time-current profiles:
- Instantaneous trip: 3-5× rated current for <100 μs response (short circuit)
- Time-delayed trip: 1.5-2× rated current for >1 second (sustained overload)
- Derated operation: 1.1-1.3× rated current with proportional load shedding
The thermal time constant τ of a battery cell determines the allowable overcurrent duration:
where Cth represents thermal capacitance and Rth the thermal resistance from junction to ambient.
Implementation Architectures
Modern BMS designs employ layered protection schemes combining:
- Analog comparators: Ultra-fast response (20-50 ns) using dedicated ICs like the LTC4365
- Digital monitoring: Microcontroller-based algorithms implementing IEC 62133 safety standards
- Hardware interlocks: Redundant MOSFET drivers with independent fault detection
The total system response time tresponse must satisfy:
where Tmax is the maximum allowable MOSFET junction temperature.
Fault Current Interruption
High-side N-channel MOSFET arrays provide the most efficient current interruption, requiring charge pumps for gate drive voltages above the battery potential. The critical design parameters include:
- MOSFET avalanche energy rating exceeding the inductive kickback energy
- Gate drive strength ensuring sub-100 ns turn-off during fault conditions
- Parallel device configurations with current sharing resistors
The minimum required MOSFET die area Amin to handle fault current Ifault for duration tfault is:
where K represents the semiconductor process constant (typically 2-5 × 104 A·s0.5/cm2·K0.75).
5. Methods for Testing Overcurrent Protection
5.1 Methods for Testing Overcurrent Protection
Controlled Load Testing
Controlled load testing involves applying a precisely measured current to the protection circuit while monitoring its response. A programmable power supply or electronic load is used to incrementally increase the current until the protection mechanism triggers. The key parameters measured are:
- Trip current (Itrip): The current at which the protection activates
- Response time (tresponse): Time delay between fault detection and activation
- Hysteresis: Difference between trip and reset currents
where α represents the tolerance band (typically 10-20%). High-precision current shunts (0.1% tolerance or better) should be used for measurement, with sampling rates exceeding 1 MS/s to capture fast transients.
Pulse Testing
Pulse testing evaluates the circuit's ability to handle short-duration overcurrent events. A capacitor discharge circuit or specialized pulse generator produces current waveforms with:
- Rise times as fast as 10 ns
- Peak currents up to 100× nominal
- Controlled pulse widths from 100 ns to 100 ms
The protection circuit must distinguish between allowable inrush currents and genuine fault conditions. This requires analyzing the time-current characteristic curve:
where K is the thermal mass constant of the protected component.
Fault Insertion Testing
This method physically creates fault conditions at strategic points in the circuit:
- Low-resistance shorts (≤10 mΩ) across current sense resistors
- MOSFET gate drive failures creating shoot-through conditions
- Inductive kickback from sudden load disconnection
High-speed oscilloscopes (≥500 MHz bandwidth) with isolated probes capture the protection response. Special attention is paid to:
- False triggering on noise spikes
- Current sharing in parallel protection devices
- Voltage transients during fault clearance
Thermal Stress Testing
Overcurrent protection must remain reliable across temperature extremes. Testing involves:
- Temperature cycling (-40°C to +125°C) while monitoring trip thresholds
- Thermal imaging of current-carrying components during faults
- Accelerated aging at 150% rated current
The Arrhenius equation predicts lifetime degradation:
where AF is acceleration factor, Ea is activation energy (typically 0.7-1.1 eV for semiconductors), and k is Boltzmann's constant.
Automated Production Testing
For volume manufacturing, automated test systems perform:
- 100% trip current verification using high-speed DAC/ADC loops
- Statistical process control (SPC) on protection parameters
- Boundary scan testing of digital protection ICs
Test sequences must verify both normal operation and fault response within tight production cycle times (typically <500 ms per test).
5.2 Common Issues and Solutions
False Triggering Due to Noise
High-frequency noise or transients can cause false triggering in overcurrent protection circuits, particularly those using comparator-based detection. The root cause often lies in insufficient filtering or poor PCB layout practices. A first-order analysis of noise susceptibility can be derived from the signal-to-noise ratio (SNR) at the comparator input:
where Vsignal is the current-sense voltage and Vnoise is the integrated noise over the bandwidth of interest. For reliable operation, SNR should exceed 20 dB. Practical solutions include:
- Adding an RC low-pass filter with cutoff frequency below the noise spectrum
- Implementing hysteresis in the comparator circuit
- Using twisted-pair wiring for current sense lines
Thermal Runaway in Solid-State Protection
MOSFET-based protection circuits face thermal challenges during prolonged overcurrent events. The power dissipation follows:
This quadratic relationship means small increases in current cause dramatic temperature rises. The thermal time constant (τ) of the package determines how quickly heat dissipates:
where RθJC is junction-to-case thermal resistance and CθJC is thermal capacitance. Effective mitigation strategies include:
- Implementing pulse-by-pulse current limiting
- Using MOSFETs with lower RDS(on) at elevated temperatures
- Adding thermal shutdown circuitry
Response Time Limitations
The theoretical minimum response time tresponse of an overcurrent protection circuit is constrained by:
where Lpar is parasitic inductance in the current path, Rsense is the sense resistor value, and tprop is the propagation delay through the protection circuitry. In high-di/dt applications (e.g., motor drives), this can lead to destructive overshoots before the protection engages. Advanced solutions employ:
- Predictive current monitoring algorithms
- Active gate drive control for faster turn-off
- Saturable reactors to limit di/dt
Ground Loop Interference
Improper grounding in current-sense circuits creates measurement errors through common-mode voltage (VCM) effects. The error voltage Verror appears as:
where CMRR is the common-mode rejection ratio of the sensing circuit. For high-side current sensing, this becomes particularly problematic. Modern approaches include:
- Using isolated current sensors (Hall-effect or fluxgate)
- Implementing fully differential amplifier topologies
- Employing digital isolation for the sense signal
Component Stress During Fault Clearing
When interrupting high currents, protection devices experience extreme stress. The let-through energy I2t must be carefully evaluated:
This parameter determines whether components will survive the fault event. For semiconductor devices, the safe operating area (SOA) provides critical boundaries. Design improvements focus on:
- Cascading protection devices (e.g., fuse + MOSFET)
- Using avalanche-rated transistors
- Implementing active current clamping
5.3 Tools and Equipment for Troubleshooting
Essential Test Instruments
Effective troubleshooting of overcurrent protection circuits requires precise measurement tools. A digital multimeter (DMM) is indispensable for measuring voltage drops across current-sensing resistors, verifying fuse integrity, and confirming proper grounding. High-end DMMs with True RMS capability ensure accurate readings in nonlinear load conditions. For dynamic analysis, an oscilloscope with bandwidth exceeding 100 MHz is recommended to capture transient current spikes and observe the response time of protection elements like PTC thermistors or electronic fuses.
Current Measurement Techniques
Non-invasive current measurement is often preferred to avoid disrupting the circuit. A Hall-effect current probe provides galvanic isolation and can measure DC or AC currents up to several hundred amps. For higher precision in low-current circuits (< 1 A), a current shunt resistor with Kelvin connections minimizes measurement errors. The voltage drop across the shunt is given by:
where Rshunt must be sufficiently small to avoid excessive power dissipation (P = I²R).
Thermal Imaging and Analysis
Overcurrent conditions often manifest as localized heating. An infrared thermal camera with spatial resolution ≤ 1.5 mRad can identify hotspots in current-carrying traces, connectors, or protection devices. For quantitative analysis, thermocouples or RTDs provide point temperature measurements with ±0.5°C accuracy. The thermal time constant (τ) of a protection device is critical:
where Rth is thermal resistance and Cth is heat capacity.
Specialized Diagnostic Tools
Advanced troubleshooting may require:
- Programmable electronic loads to simulate fault conditions with precise current ramping (e.g., 0-50 A in 1 ms)
- Insulation resistance testers (500V-1000V range) for verifying PCB creepage distances
- LCR meters to characterize the frequency-dependent impedance of crowbar circuits
Safety Considerations
When testing live circuits, use CAT III or CAT IV rated equipment for mains-connected systems. Current-limited bench power supplies with foldback protection prevent collateral damage during fault injection tests. For high-energy circuits (> 100 J), employ remote triggering and shielded enclosures.
6. Essential Books and Papers
6.1 Essential Books and Papers
- PDF Power System Protection and Switchgear - Dronacharya Group of ... — An author of four books, he has a number of papers ... 1.6 Evolution of Protective Relays 6 1.7 Zones of Protection 9 1.8 Primary and Back-up Protection 10 ... 12.3 A/D Converter, Analog Multiplexer, S/H Circuit 457 12.4 Overcurrent Relays 471 12.5 Impedance Relay 475 12.6 Directional Relay 481.
- PDF GUIDANCE NOTE Overcurrent Protection 6 - instrotech.com — thCD GN6 Protection Against Overcurrent, inc 16 Edition 2001 Amd No 1 4 SECTION 5 EQUATIONS FOR THE CALCULATION OF SHORT-CIRCUIT CURRENT 64 5.1 General equation for fault current 64 5.2 Single-phase, line to neutral fault 65 5.3 Conductor temperature and resistance 67 5.4 Single-phase circuits 72 5.5 Line to line short-circuit 73
- POWER SYSTEM RELAYING - Wiley Online Library — 8.6 Three-phase transformer protection 208 8.7 Volts-per-hertz protection 212 8.8 Nonelectrical protection 213 8.9 Protection systems for transformers 214 8.10 Summary 220 Problems 221 References 223 9 Bus, reactor and capacitor protection 225 9.1 Introduction to bus protection 225 9.2 Overcurrent relays 226 9.3 Percentage differential relays 226
- PDF C1 Overcurrent Protection for Phase and Earthfaults — Overcurrent protection, on the other hand, is directed entirely to the clearance of faults, although with the settings usually ... required between the circuit breakers at C and A in Figure C1.2. F E D C B A C B A 11 kV 250 MVA Source 200 metres 240mm2 P.I.L.C. Cable 200 metres 240mm2 P.I.L.C. Cable 4 MVA 11/3.3 kV 7%
- PDF Fundamentals of Power System Protection — 4 5 Over-current Protection 80 4.6 Percentage Differential Protection of Transformers 81 4.6 1 Development of Connections 81 4.6.2 Phase c-to-Ground (c-g) External Fault 82 4.6.3 Phase c-to-Ground (c-g) Internal Fault 84 4.7 Inrush Phenomenon 86 4.7.1 Percentage Differential Relay with Harmonic Restraint 89
- PDF Overcurrent protection - Electrical Engineering Portal — sets (mostly) or by the monitored circuit itself. 5.1 Overcurrent relays The basic element in overcurrent protection is an overcurrent relay. The ANSI device number is 50 for an instantaneous overcurrent (IOC) or a Definite Time Overcurrent (DTOC) and 51 for the Inverse Definite Minimum Time.
- PDF WHITE PAPER Residual current devices (RCDs) Protection against ... - ABB — 3.1 Basic Protection 4 3.2 Fault protection 4 3.3 Additional protection 6 4. Effects of electric current on the human body 7 4.1 Ventricular fibrillation limit 8 5. Types of RCDs 8 5.1 Residual Current Circuit Breaker (RCCB) 8 5.2 Circuit Breaker with Overload protection (RCBO) 9 5.3 Residual current relay (earth leakage relay) 9
- PDF Control Panels USA, Industrial Control Panels for North America,White paper — coupled with a supply circuit disconnecting means is necessary. • Chapter 19.1 Branch-Circuit Overcurrent Protection for Drives and Motors: Clearer formulation of the fact that short circuit protection for branch circuits with converters for servo drives shall correspond to the manufacturer's specifications. Outlook: NFPA 79 2018
- Electrical Overstress (EOS): Devices, Circuits and Systems — Electrical Overstress (EOS) continues to impact semiconductor manufacturing, semiconductor components and systems as technologies scale from micro- to nano-electronics. This bookteaches the fundamentals of electrical overstress and how to minimize and mitigate EOS failures. The text provides a clear picture of EOS phenomena, EOS origins, EOS sources, EOS physics, EOS failure mechanisms, and ...
- (PDF) RING MAIN PROTECTION - ResearchGate — This report entails the complete design process of a ring main protection system. Each design constraint has been outlined and achieved. A solution utilizing non-directional time overcurrent ...
6.2 Online Resources and Datasheets
- LM76202-Q1 60-V, 2.2-A Integrated Ideal Diode with Overvoltage and ... — 8.1 Overview LM76202-Q1 is an ideal diode with integrated back-to-back FETs and enhanced built-in protection circuitry. It provides robust protection for all systems and applications powered from 4.2 V to 60 V. The device integrates reverse battery input, reverse current, overvoltage, undervoltage, overcurrent and short circuit protection.
- PDF Datasheet - OCVPB21-13F6 - ESD, overvoltage and overcurrent protection ... — The OCVPB21-13F6 is an integrated ESD, overvoltage and overcurrent protection with an integrated input rectification bridge to give flexibility for wearable and IoT customers to manage properly any kind of USB charging conditions with or without USB cable inversion.
- Chapter 6 Design and Implementation of Overcurrent, Pilot ... - Springer — This section describes the design of the line protection system for two-terminal lines with at least the following protection functions: † Three-phase directional instantaneous overcurrent relays for the primary protection. † Three-phase time overcurrent relays for the backup protection. † Residual time overcurrent relay.
- PDF Overcurrent Protection — Application The SIPROTEC easy 7SJ45 is a numerical overcurrent protection relay which is pri-marily intended as a radial feeder or trans-former protection (backup) in electrical networks. It provides definite-time and inverse-time overcurrent protection according to IEC and ANSI standards.
- PDF L6206.fm - STMicroelectronics — 5.3 Non-dissipative overcurrent detection and protection In addition to the PWM current control, an overcurrent detection circuit (OCD) is integrated. This circuit can be used to provide protection against a short-circuit to ground or between two phases of the bridge as well as a roughly regulation of the load current.
- PDF Overcurrent protection - Electrical Engineering Portal — The basic element in overcurrent protection is an overcurrent relay. The ANSI device number is 50 for an instantaneous overcurrent (IOC) or a Definite Time Overcurrent (DTOC) and 51 for the Inverse Definite Minimum Time.
- Overcurrent Protection Circuit using Op-Amp — There are many types of over-current protection circuits; the complexity of the circuit depends on how fast the protection circuit should react during an over-current situation. In this project, we will build a simple over-current protection circuit using an op-amp which is very commonly used and can be easily adapted for your designs.
- 4230-t (Ul 489) | E-t-a — Differences and Similarities Between K Curve and D Curve Breakers A Miniature Circuit Breaker (MCB) is a resettable protective device that prevents electrical circuits from catching fire and causing damage to personnel and property. It is a device designed to isolate a circuit during an overcurrent event without using a fusible element.
- PDF Overvoltage and Overcurrent Protection IC, Li+ Charger Front-End ... — The bq24314C device is a highly integrated circuit (IC) designed to provide protection to Li-ion batteries from failures of the charging circuit. The device continuously monitors the input voltage, the input current, and the battery voltage.
- PDF 00-GN6-Against Overcurrent-Prelims.indd - RS Components — 46 Short-circuit rating of low voltage assemblies (switchboards, panel boards, distribution boards, etc.) 3.5 Position of fault current protection and assessment of
6.3 Industry Standards and Guidelines
- PDF IEC 60364-4-43:2023 - IEC 60364-4-43:2023 - iTeh Standards — STANDARD NORME INTERNATIONALE Low-voltage electrical installations - Part 4-43: Protection for safety - Protection against overcurrent . Installations électriques à basse tension - Partie 4-43: Protection pour assurer la sécurité - Protection contre les surintensités . IEC 60364-4-43: 202 3-0 7 (en-fr) ® L7HK67$$ 1' $$ 5' 3 5( 9,( :
- PDF GUIDANCE NOTE Overcurrent Protection 6 - NIRMT — SECTION 1 THE REGULATIONS CONCERNING PROTECTION AGAINST OVERCURRENT 10 1.1 Scope 10 1.2 Nature of overcurrent and protection 11 1.3 Statutory requirements 13 1.4 Omission of protection 13 1.5 Protective devices 14 1.6 Duration of overcurrent 14 1.7 Co-ordination and discrimination 15 SECTION 2 PROTECTION AGAINST OVERLOAD 20 2.1 General 20
- PDF GUIDANCE NOTE Overcurrent Protection 6 - instrotech.com — thCD GN6 Protection Against Overcurrent, inc 16 Edition 2001 Amd No 1 4 SECTION 5 EQUATIONS FOR THE CALCULATION OF SHORT-CIRCUIT CURRENT 64 5.1 General equation for fault current 64 5.2 Single-phase, line to neutral fault 65 5.3 Conductor temperature and resistance 67 5.4 Single-phase circuits 72 5.5 Line to line short-circuit 73
- Understanding the IEC 62368-1 standard for electronic equipment — Universal power adapters, commonly used in IT equipment, accept a wide range of voltage inputs, such as 90 to 240 VAC. This voltage range allows the product to be used worldwide with a common set of electronics. Safety requirements dictated by IEC 62368-1 require both overcurrent and surge protection. Overcurrent protection
- System Protection - 0100DB2301 Electrical Distribution Fundamentals ... — Electronic trip circuit breaker: ... Instantaneous overcurrent relays have no inherent time delay and are used for fast short-circuit protection. 50 and 51 Overcurrent Relay Characteristics shows the timing characteristics of several typical 51 time-overcurrent ... Standard overcurrent relays cannot distinguish the direction of the current flow
- PDF A Guide to United States Electrical and Electronic Equipment ... - NIST — This guide addresses electrical and electronic consumer products, including those that will . In addition, it includes electrical and electronic products used in the workplace as well as electrical and electronic medical devices. The scope does not include vehicles or components of vehicles, electric or electronic toys, or recycling ...
- Guidance Note 6 - Protection Against Overcurrent (IEE Guidence Notes ... — Guidance Note 6_ Protection Against Overcurrent (IEE Guidence Notes) (No 6) ( PD - Free download as PDF File (.pdf), Text File (.txt) or read online for free. This document discusses calculating three-phase short-circuit currents for protective device selection. It provides equations to calculate the current based on line impedance values, which can be estimated from tables in BS7671 using ...
- PDF Best Protection Practices For HV and EHV Transmission Systems of ENTSO ... — technical guidelines refer all voltage levels unless mentioned otherwise . Note 2: In present text protection systems are considered as integrated and include one or more protection equipments, instrument transformer(s), wiring, tripping circuit(s), auxiliary supply(s) and, where provided, communication system(s).
- PDF Addressing 2021 NFPA 99 updates to electrical system ... - Eaton — The National Fire Protection Association's Health Care Facilities Code (NFPA 99) is one of the industry's most important set of safety guidelines. For decades, it has continuously evolved to help reduce fire, explosion and electricity hazards for patients, staff, or visitors across all healthcare environments.
- PDF PSS Part 5 OC 0106 Cover - Electrical Engineering Portal — "The overcurrent protective devices, the total impedance, the component short-circuit current ratings, and other characteristics of the circuit to be protected shall be selected and coordinated to permit the circuit-protective devices used to clear a fault to do so without extensive damage to the electrical components of the circuit.