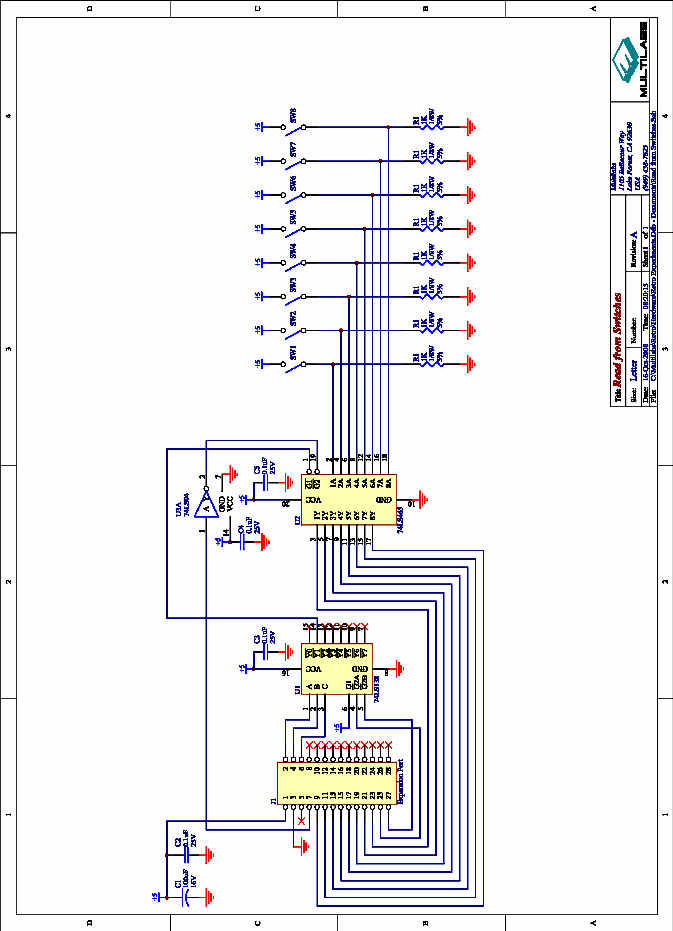
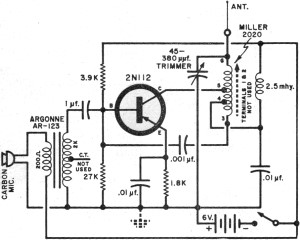
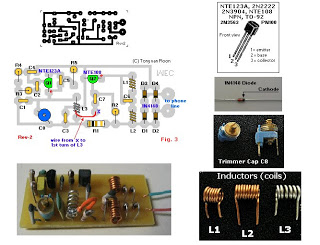
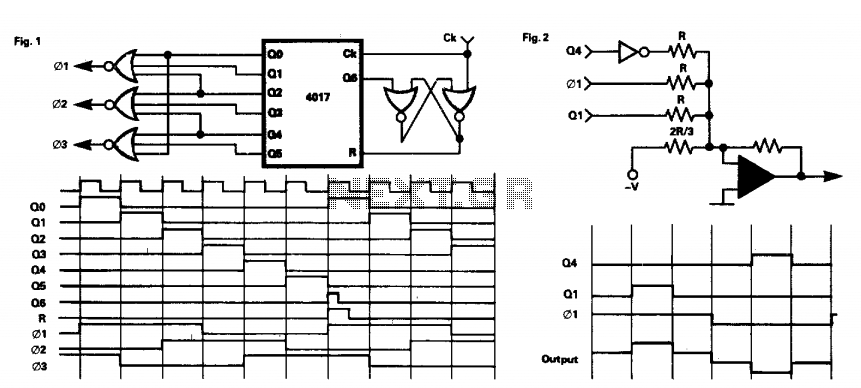
Phase shift AC Circuits

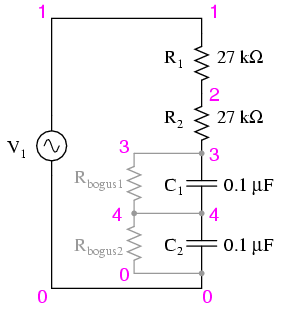
Construct the circuit and measure the voltage drops across each component using an AC voltmeter. Additionally, measure the total (supply) voltage with the same voltmeter. It will be observed that the individual voltage drops do not sum up to the total voltage. This discrepancy arises from phase shifts within the circuit: the voltage across the capacitors is out of phase with the voltage across the resistors, leading to unexpected results. When considering the phase angle, the voltages do sum to equal the total, but a voltmeter only measures amplitude and does not account for phase angles. It is recommended to measure the voltage drop across both resistors simultaneously; this combined voltage drop will equal the sum of the individual voltage drops across each resistor. This indicates that the voltage drop waveforms for both resistors are in phase. Similarly, measure the voltage drop across both capacitors at once; this combined voltage drop will also equal the sum of the individual voltage drops across each capacitor. This confirms that the voltage drop waveforms for both capacitors are in phase as well. Given that the power supply frequency is 60 Hz (the standard household frequency in the United States), calculate the impedances for all components and determine all voltage drops using Ohm's Law (E=IZ; I=E/Z; Z=E/I). The polar magnitudes of the results should closely align with the readings from the voltmeter.

In constructing an AC circuit, it is essential to understand the behavior of various components under alternating current conditions. The circuit typically consists of resistors and capacitors, where the resistors exhibit a purely resistive behavior, while the capacitors introduce reactance that causes phase shifts between voltage and current.

When measuring voltage drops across components, the use of an AC voltmeter is crucial. The voltmeter provides measurements of the root mean square (RMS) values of the voltages, which are representative of the effective values in an AC circuit. As the measurements are taken, it becomes evident that the voltage drops across the capacitors and resistors do not simply add up to the supply voltage due to the phase differences.

To analyze the circuit accurately, it is beneficial to measure voltage drops across both resistors simultaneously. This measurement confirms that the voltage drops are in phase, as their combined value equals the sum of the individual readings. A similar approach applies to capacitors, where measuring the voltage drop across both at once reveals that their waveforms are also in phase, ensuring their combined voltage drop reflects the sum of the individual capacitor voltage drops.

In the context of a 60 Hz power supply frequency, calculations of impedance for each component can be performed. The impedance (Z) of a resistor is simply its resistance (R), while the impedance of a capacitor can be calculated using the formula Z = 1/(2πfC), where f is the frequency and C is the capacitance. Once impedances are determined, voltage drops can be calculated using Ohm's Law, which relates voltage (E), current (I), and impedance (Z).

The final values obtained from these calculations should align closely with the voltmeter readings, confirming the accuracy of the measurements and the theoretical predictions of the circuit behavior. This exercise highlights the importance of considering both amplitude and phase in AC circuit analysis, providing a comprehensive understanding of voltage relationships within the circuit.Build the circuit and measure voltage drops across each component with an AC voltmeter. Measure total (supply) voltage with the same voltmeter. You will discover that the voltage drops do not add up to equal the total voltage. This is due to phase shifts in the circuit: voltage dropped across the capacitors is out-of-phase with voltage dropped acr oss the resistors, and thus the voltage drop figures do not add up as one might expect. Taking phase angle into consideration, they do add up to equal the total, but a voltmeter doesn`t provide phase angle measurements, only amplitude. Try measuring voltage dropped across both resistors at once. This voltage drop will equal the sum of the voltage drops measured across each resistor separately. This tells you that both the resistors` voltage drop waveforms are in-phase with each other, since they add simply and directly.

Measure voltage dropped across both capacitors at once. This voltage drop, like the drop measured across the two resistors, will equal the sum of the voltage drops measured across each capacitor separately. Likewise, this tells you that both the capacitors` voltage drop waveforms are in-phase with each other.

Given that the power supply frequency is 60 Hz (household power frequency in the United States), calculate impedances for all components and determine all voltage drops using Ohm`s Law (E=IZ ; I=E/Z ; Z=E/I). The polar magnitudes of the results should closely agree with your voltmeter readings. 🔗 External reference