PWM Signal Generation

1. Definition and Basic Principles of PWM

Definition and Basic Principles of PWM

Pulse-width modulation (PWM) is a technique for encoding analog signal levels into a digital signal by varying the duty cycle of a square wave. The duty cycle (D) represents the fraction of time the signal remains in the high state relative to the total period (T). Mathematically, it is defined as:

$$ D = \frac{t_{\text{on}}}{T} \times 100\% $$

where ton is the duration the signal is active (high). The frequency (f) of the PWM signal is the inverse of the period:

$$ f = \frac{1}{T} $$

Fundamental Waveform Characteristics

A PWM signal is characterized by three primary parameters:

For a given period T, the signal remains high for ton = D × T and low for toff = (1 - D) × T.

Average Voltage Representation

When a PWM signal drives a load with a sufficiently high frequency, the effective (average) voltage (Vavg) perceived by the load is proportional to the duty cycle:

$$ V_{\text{avg}} = D \times V_p $$

This principle allows PWM to emulate analog voltage levels using digital switching, making it highly efficient for power delivery in applications like motor control, LED dimming, and DC-DC converters.

Fourier Analysis of PWM Signals

From a spectral perspective, a PWM signal contains harmonic components centered around the switching frequency. The Fourier series expansion of a PWM waveform with duty cycle D and amplitude Vp is given by:

$$ V(t) = D V_p + \sum_{n=1}^{\infty} \frac{2 V_p}{n \pi} \sin(n \pi D) \cos(2 \pi n f t) $$

The first term represents the DC component (average voltage), while the summation captures the harmonic content. Filtering can suppress higher harmonics, leaving only the desired analog-equivalent output.

Practical Considerations

Key design factors in PWM systems include:

PWM is widely used in power electronics due to its efficiency, precision, and compatibility with digital control systems. Applications range from servo motor control to switch-mode power supplies and Class-D audio amplification.

1.2 Duty Cycle and Frequency in PWM

The fundamental parameters defining a Pulse Width Modulation (PWM) signal are its duty cycle and frequency. These two variables govern the behavior of PWM in applications ranging from motor control to power regulation and signal modulation.

Mathematical Definition of Duty Cycle

The duty cycle (D) of a PWM signal is the ratio of the pulse width (Ï„) to the total period (T) of the signal, expressed as a percentage:

$$ D = \left( \frac{\tau}{T} \right) \times 100\% $$

For instance, a 50% duty cycle means the signal is high for half the period and low for the remaining half. In power delivery applications, the duty cycle directly determines the average voltage delivered to a load:

$$ V_{avg} = D \times V_{max} $$

Frequency and Its Impact on System Performance

The frequency (f) of a PWM signal is the inverse of its period:

$$ f = \frac{1}{T} $$

Higher frequencies reduce ripple in power applications but increase switching losses in transistors. Conversely, lower frequencies minimize switching losses but may introduce undesirable harmonics or audible noise in motor control systems.

Trade-offs in Duty Cycle and Frequency Selection

Selecting optimal PWM parameters involves balancing several factors:

Practical Considerations in PWM Generation

Modern microcontrollers and dedicated PWM controllers implement duty cycle and frequency control through timer-based registers. For example, an 8-bit PWM resolution allows 256 discrete duty cycle steps (0–100%), while the timer overflow rate sets the frequency. The achievable frequency is constrained by the clock speed and prescaler settings:

$$ f_{PWM} = \frac{f_{clock}}{N \cdot (TOP + 1)} $$

where N is the prescaler divider and TOP is the timer's maximum count value.

In motor drive applications, dead-time insertion between complementary PWM signals prevents shoot-through currents in H-bridge configurations. This requires precise synchronization between duty cycle adjustments and the switching frequency.

PWM Waveform Characteristics Time-domain plot of PWM waveforms with varying duty cycles (25%, 50%, 75%), showing the relationship between pulse width (Ï„), period (T), and duty cycle (D). Time Voltage 0 Vmax 25% Duty Cycle (D=0.25) Ï„ T (Period) 50% Duty Cycle (D=0.5) Ï„ 75% Duty Cycle (D=0.75) Ï„ Vavg (25%) Vavg (50%) Vavg (75%)
Diagram Description: The diagram would show the visual relationship between duty cycle, period, and pulse width in a PWM waveform, and how different duty cycles affect the signal's high/low states over time.

1.3 Applications of PWM in Electronics

Power Delivery and Voltage Regulation

PWM is fundamental in switch-mode power supplies (SMPS), where it controls the duty cycle of switching transistors to regulate output voltage. A buck converter, for instance, steps down voltage by adjusting the PWM duty cycle D such that:

$$ V_{out} = D \times V_{in} $$

High-frequency PWM (kHz to MHz) minimizes inductor and capacitor sizes, enabling compact power supplies. Advanced topologies like interleaved PWM reduce ripple current by phase-shifting multiple PWM signals.

Motor Control

In brushless DC (BLDC) and stepper motors, PWM modulates phase currents to control torque and speed. Field-oriented control (FOC) algorithms use PWM to generate sinusoidal currents with precise amplitude and phase:

$$ I_q = K_t \times \tau_{desired} $$

where Iq is the quadrature current component. Dead-time insertion in PWM signals prevents shoot-through in H-bridge inverters.

Audio Amplification

Class-D amplifiers leverage PWM to encode audio signals into high-frequency square waves. The output is filtered to reconstruct the analog waveform with efficiencies exceeding 90%. Key metrics include:

LED Dimming and Color Control

PWM achieves high-resolution dimming (16-bit+) for LEDs without chromaticity shifts. In RGB systems, PWM duty cycles for red, green, and blue channels determine the mixed color coordinates in CIE 1931 space:

$$ \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = \sum_{i=R,G,B} D_i \cdot \begin{pmatrix} X_i \\ Y_i \\ Z_i \end{pmatrix} $$

RF and Communication Systems

PWM underpins envelope tracking in RF power amplifiers, where the supply voltage dynamically adjusts to match the signal envelope. This reduces DC power consumption by up to 30% in 5G base stations. PWM-based sigma-delta modulators also enable digital-to-analog conversion with >100 dB dynamic range.

Precision Heating Systems

Thermal controllers use PWM to maintain temperatures within ±0.1°C by modulating heater power. The duty cycle correlates with thermal time constants:

$$ \tau_{thermal} = R_{th}C_{th} $$

where Rth and Cth are the thermal resistance and capacitance.

2. Using Microcontrollers for PWM

Using Microcontrollers for PWM

Hardware PWM Modules in Microcontrollers

Most modern microcontrollers integrate dedicated PWM hardware modules, such as timers with capture/compare units. These modules offload the PWM generation task from the CPU, enabling precise waveform generation without software overhead. For example, ARM Cortex-M processors typically feature multiple 16-bit or 32-bit timers with up to 6 PWM channels per timer.

The PWM resolution is determined by the timer's counter register size. For an n-bit counter, the duty cycle can be adjusted in steps of:

$$ \Delta D = \frac{100\%}{2^n - 1} $$

Register-Level Configuration

Configuring hardware PWM involves setting several registers:

For a 16-bit timer running at 72 MHz, the minimum achievable PWM frequency is:

$$ f_{min} = \frac{f_{clock}}{2^{16}} = \frac{72 \text{ MHz}}{65536} \approx 1.1 \text{ kHz} $$

Dead-Time Insertion

In motor control and bridge circuits, dead-time prevents shoot-through currents. Advanced PWM modules include hardware dead-time generators that insert a programmable delay between complementary PWM signals. The dead-time duration td is typically configured through a dedicated register:

$$ t_d = \frac{DTG \cdot t_{clock}}{f_{prescaler}} $$

where DTG is the dead-time generator value and tclock is the system clock period.

Advanced Microcontroller Features

Recent microcontroller families offer enhanced PWM capabilities:

Software-Based PWM Implementation

When hardware PWM channels are exhausted, software PWM can be implemented using:

The maximum achievable software PWM frequency is constrained by interrupt latency. For a system with interrupt response time tirq, the theoretical maximum frequency is:

$$ f_{max} = \frac{1}{2 \cdot t_{irq}} $$

Synchronization Techniques

Multi-phase PWM systems require precise synchronization between channels. Microcontrollers achieve this through:

The timing skew between synchronized channels is typically less than 1% of the PWM period when using hardware synchronization.

Microcontroller PWM Hardware Module Block Diagram Block diagram showing PWM signal generation with timer control register, auto-reload register, capture/compare register, dead-time generator, and PWM output waveform. TCR ARR CCR Clock Prescaler DTG PWM_OUT PWM Output Waveform (Duty Cycle: 50%)
Diagram Description: The section covers hardware PWM module configurations and timing relationships, which are highly visual concepts involving register interactions and waveform generation.

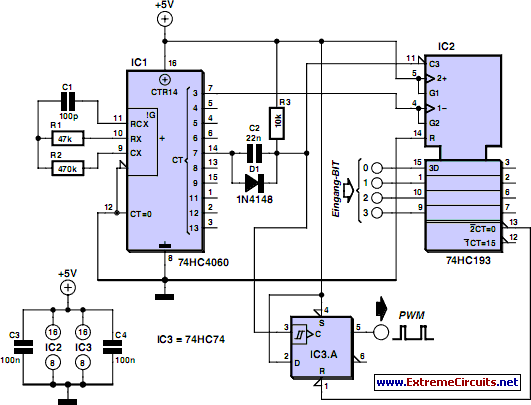
2.2 Dedicated PWM ICs and Modules

Architecture of Dedicated PWM Controllers

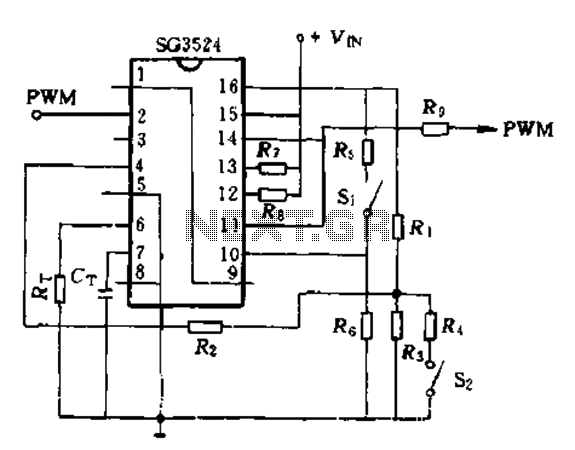
Dedicated PWM ICs integrate precision timing circuits, error amplifiers, and output drivers into a single package. The TL494 and SG3525 are classic examples featuring:

The duty cycle (D) is determined by comparing a sawtooth waveform (Vramp) with a control voltage (Vctrl):

$$ D = \frac{V_{ctrl}}{V_{ramp(max)}} \times 100\% $$

Modern PWM Modules: Digital vs. Hybrid

Contemporary modules like the MAX1556 (digital) and LT6992 (hybrid) combine analog precision with digital programmability. Key advancements include:

Case Study: Digital PWM Resolution

For a 16-bit PWM running at 1 MHz, the time resolution (Δt) is:

$$ \Delta t = \frac{1}{f_{PWM} \times \frac{1}{2^n} = \frac{1}{1 \text{MHz}} \times \frac{1}{65536} = 15.26 \text{ps} $$

Thermal and Power Considerations

High-frequency operation (≥500 kHz) requires careful thermal management. Power dissipation in a PWM driver with RDS(on) = 50 mΩ and IRMS = 3A is:

$$ P_{loss} = I_{RMS}^2 \times R_{DS(on)} = 9 \times 0.05 = 450 \text{mW} $$
Typical PWM IC Thermal Derating Curve

Application-Specific PWM ICs

Specialized variants address niche requirements:

Noise and Jitter Performance

High-end PWM generators like the Si8261 achieve jitter below 50 ps RMS by using:

PWM Duty Cycle Determination A diagram showing how PWM duty cycle is determined by comparing a sawtooth waveform (V_ramp) with a control voltage (V_ctrl). The resulting PWM signal is displayed below. Time Voltage Time PWM V_ramp V_ramp(max) V_ctrl Intersection Intersection PWM Output D Period (T)
Diagram Description: The section explains how duty cycle is determined by comparing a sawtooth waveform with a control voltage, which is inherently visual.

2.3 Analog PWM Generation Techniques

Analog PWM generation relies on continuous-time signal processing to modulate the duty cycle of a pulse train in response to an input voltage. Unlike digital methods, which rely on discrete-time counters and comparators, analog techniques exploit the natural behavior of operational amplifiers, comparators, and nonlinear feedback loops to produce a PWM signal with high resolution and minimal quantization noise.

Core Principle: Triangle Wave Modulation

The most common analog PWM method involves comparing a modulating signal (typically an audio or control voltage) with a high-frequency triangle or sawtooth carrier wave. The intersection points between these signals determine the switching instants, translating the input amplitude into a proportional duty cycle.

$$ D(t) = \frac{V_{in}(t) - V_{min}}{V_{max} - V_{min}} $$

where D(t) is the instantaneous duty cycle, Vin(t) is the input signal, and Vmin, Vmax define the carrier's peak-to-peak range. The triangle wave's linearity directly impacts PWM distortion, with nonlinearities introducing harmonic artifacts.

Circuit Implementation: Op-Amp Based Generators

A classic implementation uses an integrator to generate the triangle wave and a comparator for modulation:

Nonlinear Effects and Compensation

Real-world integrators exhibit slew rate limiting and capacitor dielectric absorption, distorting the triangle wave. Compensation techniques include:

$$ f_{carrier} = \frac{1}{4RC \ln \left( \frac{1 + \beta}{1 - \beta} \right)} $$

where β is the feedback factor accounting for nonlinearities.

Advanced Techniques: Voltage-to-Frequency Conversion

For applications requiring variable frequency alongside duty cycle modulation (e.g., resonant converters), voltage-controlled oscillators (VCOs) like the 4046 PLL IC generate a carrier whose frequency is proportional to Vin. The resulting PWM spectrum becomes adaptive, reducing EMI in sensitive applications.

Practical Considerations

Analog PWM Generation Waveforms Waveform diagram showing the relationship between a triangle carrier wave, input signal, and resulting PWM output for analog pulse-width modulation. Time Voltage Time Voltage Triangle Wave Input Signal PWM Output V_max V_min D(t) Switching Points
Diagram Description: The diagram would show the relationship between the triangle wave, input signal, and resulting PWM output waveforms to visualize the modulation process.

3. PWM Generation Using Embedded Software

3.1 PWM Generation Using Embedded Software

Fundamentals of Software-Based PWM

Pulse-width modulation (PWM) generation via embedded software relies on precise timing control through microcontroller peripherals such as timers and compare registers. The duty cycle D is defined as the ratio of the pulse width ton to the total period T:

$$ D = \frac{t_{on}}{T} \times 100\% $$

Modern microcontrollers implement PWM through hardware-assisted software control, where timer interrupts or direct memory access (DMA) updates duty cycle values stored in capture/compare registers. The resolution of the PWM signal is determined by the counter register's bit depth:

$$ \text{Resolution (bits)} = \log_2 \left( \frac{f_{\text{clock}}}{f_{\text{PWM}}} \right) $$

Implementation Strategies

Two primary methods exist for software PWM generation:

Timer Interrupt Method

For microcontrollers without dedicated PWM hardware, a timer interrupt service routine (ISR) can manually set and clear output pins. The ISR must:

  1. Increment a counter variable
  2. Compare the counter against the desired duty cycle value
  3. Set the output high when counter ≤ duty value
  4. Clear the output when counter > duty value
  5. Reset the counter at the period boundary

// Example ARM Cortex-M timer ISR for PWM generation
void TIM2_IRQHandler(void) {
   static uint16_t pwm_counter = 0;
   pwm_counter++;
   
   if (pwm_counter <= duty_cycle) {
      GPIO_SetPin(PWM_OUTPUT_PIN);
   } else {
      GPIO_ClearPin(PWM_OUTPUT_PIN);
   }
   
   if (pwm_counter >= PWM_PERIOD) {
      pwm_counter = 0;
   }
   
   TIM_ClearFlag(TIM2, TIM_FLAG_Update);
}

Hardware-Assisted PWM

Modern microcontrollers like STM32 or ESP32 provide dedicated PWM timer blocks that only require software initialization:

  1. Configure timer clock source and prescaler
  2. Set auto-reload register (ARR) for period
  3. Set capture/compare register (CCR) for duty cycle
  4. Enable PWM output mode on GPIO
  5. Start the timer

// STM32 HAL library PWM initialization
TIM_HandleTypeDef htim;
TIM_OC_InitTypeDef sConfigOC;

htim.Instance = TIM1;
htim.Init.Prescaler = 0;
htim.Init.CounterMode = TIM_COUNTERMODE_UP;
htim.Init.Period = 999; // 1kHz PWM with 1MHz clock
htim.Init.ClockDivision = TIM_CLOCKDIVISION_DIV1;
HAL_TIM_PWM_Init(&htim);

sConfigOC.OCMode = TIM_OCMODE_PWM1;
sConfigOC.Pulse = 250; // 25% duty cycle
sConfigOC.OCPolarity = TIM_OCPOLARITY_HIGH;
sConfigOC.OCFastMode = TIM_OCFAST_DISABLE;
HAL_TIM_PWM_ConfigChannel(&htim, &sConfigOC, TIM_CHANNEL_1);

HAL_TIM_PWM_Start(&htim, TIM_CHANNEL_1);

Advanced Techniques

For high-resolution PWM, consider these optimizations:

The maximum achievable PWM frequency is constrained by both the timer clock speed and the required resolution:

$$ f_{\text{PWM(max)}} = \frac{f_{\text{clock}}}{2^{\text{resolution}}} $$

For example, a 72MHz clock with 16-bit resolution yields a maximum frequency of approximately 1.1kHz while maintaining full resolution. Higher frequencies require either reduced resolution or advanced prescaling techniques.

PWM Generation Methods Comparison A comparison diagram of PWM signal generation methods, showing timer interrupt flow, hardware PWM block, and aligned PWM waveforms with duty cycle variations. Timer ISR Flow Timer Overflow Update CCR Set GPIO Hardware PWM Block CLK Prescaler ARR CCR GPIO PWM Output Waveforms T t_on T t_on Clock
Diagram Description: The section describes timing relationships and PWM signal generation methods that would benefit from visual representation of waveforms and hardware block interactions.

3.2 Algorithmic Approaches to PWM

Mathematical Basis of PWM Generation

Pulse-width modulation (PWM) generation relies on precise timing control, where the duty cycle D is defined as the ratio of the pulse duration Ton to the total period T:

$$ D = \frac{T_{on}}{T} $$

For a desired output voltage Vout with a supply voltage VDC, the duty cycle is derived as:

$$ V_{out} = D \cdot V_{DC} $$

This linear relationship forms the foundation of most PWM algorithms, where precise control of D enables accurate voltage or power regulation.

Counter-Based PWM Algorithms

Digital PWM generation often employs a counter-comparator approach. A free-running N-bit counter increments at a clock frequency fclk, producing a sawtooth waveform. The PWM period T is determined by:

$$ T = \frac{2^N}{f_{clk}} $$

A comparator triggers the output transition when the counter matches a duty cycle register value Dreg. This method is widely used in microcontrollers and FPGA-based systems due to its deterministic timing and low computational overhead.

Delta-Sigma Modulation for High-Resolution PWM

When higher resolution is required than native counter bits allow, delta-sigma modulation can be employed. This technique uses noise shaping to push quantization error to higher frequencies, achieving effective resolutions beyond hardware limitations. The first-order delta-sigma modulator follows:

$$ y[n] = \begin{cases} 1 & \text{if } x[n] - \sum_{k=1}^{n-1} (x[k] - y[k]) \geq 0 \\ 0 & \text{otherwise} \end{cases} $$

where x[n] is the input signal and y[n] is the PWM output. This approach is particularly effective in audio amplification and precision motor control applications.

Space Vector PWM for Three-Phase Systems

In three-phase inverters, space vector PWM (SVPWM) provides superior DC bus utilization compared to sinusoidal PWM. The algorithm:

  1. Transforms three-phase voltages to α-β coordinates
  2. Determines the sector in the space vector hexagon
  3. Calculates dwell times for adjacent active vectors and zero vectors

The voltage vector Vref is synthesized using:

$$ \mathbf{V}_{ref} = \frac{T_1}{T_s}\mathbf{V}_1 + \frac{T_2}{T_s}\mathbf{V}_2 $$

where T1 and T2 are the dwell times for vectors V1 and V2, and Ts is the switching period.

Predictive PWM Control

Model predictive control (MPC) algorithms optimize PWM generation by evaluating future system states. The cost function:

$$ J = \sum_{k=1}^{N_p} \left( \| \mathbf{x}^*(k) - \mathbf{x}(k) \|^2_{\mathbf{Q}} + \| \Delta \mathbf{u}(k) \|^2_{\mathbf{R}} \right) $$

minimizes tracking error x* - x while penalizing control effort Δu, with prediction horizon Np and weighting matrices Q, R. This approach provides fast dynamic response in power electronic converters.

Hardware Implementation Considerations

When implementing PWM algorithms in hardware, several factors must be considered:

PWM Algorithm Visualizations A multi-panel diagram illustrating PWM signal generation, including a sawtooth counter waveform, comparator output, space vector hexagon with sectors, voltage vectors, and a delta-sigma modulator block diagram. Counter-Based PWM Generation D T Output PWM Signal N-bit Counter Space Vector PWM (SVPWM) α β V1 V2 Vref Sector 1 Delta-Sigma Modulator Σ Q DAC -1 Input Output Quantization Error
Diagram Description: The section involves spatial relationships (space vector PWM hexagon), time-domain waveforms (counter-based PWM), and vector math (SVPWM) that require visual representation.

3.3 Simulation of PWM in Software Environments

Mathematical Foundation of PWM Simulation

Simulating pulse-width modulation (PWM) in software requires a precise mathematical representation of the signal. The PWM waveform is characterized by its duty cycle D, period T, and amplitude A. The duty cycle is defined as the ratio of the pulse width Ï„ to the period:

$$ D = \frac{\tau}{T} $$

In discrete-time simulation, the PWM signal is sampled at a frequency fs, where fs must be significantly higher than the PWM frequency fPWM = 1/T to avoid aliasing. The Nyquist criterion mandates:

$$ f_s \geq 2f_{PWM} $$

However, in practice, a sampling rate of at least 10fPWM is recommended to accurately capture the rising and falling edges of the PWM signal.

Software Tools for PWM Simulation

Several software environments are commonly used for PWM simulation, each with unique advantages:

Implementation in MATLAB/Simulink

In Simulink, PWM generation can be implemented using the Pulse Generator block or through a custom comparator-based approach. The comparator method compares a modulating signal (e.g., sine wave) with a high-frequency carrier (typically triangular):

$$ \text{PWM}(t) = \begin{cases} A & \text{if } V_{\text{mod}}(t) \geq V_{\text{carrier}}(t) \\ 0 & \text{otherwise} \end{cases} $$

The following Simulink blocks are essential for accurate PWM simulation:

Python Implementation Example

For discrete-time simulation in Python, the PWM signal can be generated using NumPy and visualized with matplotlib:

import numpy as np
import matplotlib.pyplot as plt

# Parameters
f_pwm = 1e3      # PWM frequency (Hz)
f_s = 100e3      # Sampling frequency (Hz)
D = 0.75         # Duty cycle (0 to 1)
T = 1 / f_pwm    # Period (s)
t = np.arange(0, 2*T, 1/f_s)  # Time vector

# Generate PWM signal
pwm_signal = np.where(np.mod(t, T) < D * T, 1, 0)

# Plot
plt.plot(t, pwm_signal)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Simulated PWM Signal (D=0.75)')
plt.grid(True)
plt.show()

Practical Considerations

When simulating PWM in software, the following factors must be accounted for:

Validation Against Analytical Models

The simulated PWM output should be validated against the theoretical Fourier series representation of an ideal PWM signal:

$$ V_{\text{PWM}}(t) = DA + \sum_{n=1}^{\infty} \frac{2A}{n\pi} \sin(n\pi D) \cos(2\pi n f_{PWM} t) $$

Harmonic distortion analysis (e.g., THD calculation) can be performed using FFT-based methods to verify simulation accuracy.

PWM Signal Generation with Carrier and Modulating Signals A time-domain representation of PWM signal generation, showing the triangular carrier wave, modulating sine wave, and resulting PWM output signal. Time (t) T V_carrier(t) Amplitude V_mod(t) PWM(t) D PWM Signal Generation Carrier and Modulating Signals
Diagram Description: The section describes PWM signal generation through mathematical equations and software implementations, which would benefit from a visual representation of the PWM waveform and its relationship to the carrier and modulating signals.

4. Sinusoidal PWM (SPWM)

4.1 Sinusoidal PWM (SPWM)

Sinusoidal Pulse Width Modulation (SPWM) is a modulation technique used to generate a quasi-sinusoidal output from a DC source by controlling the duty cycle of a high-frequency carrier signal. Unlike regular PWM, which produces a square wave, SPWM approximates a sine wave by varying the pulse width in proportion to the amplitude of a reference sine wave.

Mathematical Foundation

The fundamental principle of SPWM involves comparing a high-frequency triangular carrier wave (Vcarrier) with a low-frequency sinusoidal reference wave (Vref). The intersection points determine the switching instants of the PWM signal. The modulation index (ma) is defined as:

$$ m_a = \frac{V_{ref}}{V_{carrier}} $$

where:

The output voltage (Vout) of an inverter using SPWM can be expressed in terms of the DC bus voltage (VDC) and modulation index:

$$ V_{out} = m_a \cdot \frac{V_{DC}}{2} \cdot \sin(\omega t) $$

Generation Method

SPWM is typically implemented using the following steps:

  1. Carrier Wave Selection: A triangular wave with frequency fc (carrier frequency) is generated, usually at several kHz to minimize harmonic distortion.
  2. Reference Sine Wave: A sinusoidal wave with the desired output frequency fo (e.g., 50 Hz or 60 Hz) is generated.
  3. Comparator Operation: The PWM signal switches high when Vref > Vcarrier and low otherwise.

Harmonic Analysis

SPWM reduces lower-order harmonics compared to square-wave modulation. The harmonic spectrum consists of sidebands centered around multiples of the carrier frequency. The dominant harmonics occur at:

$$ f_h = k \cdot f_c \pm l \cdot f_o $$

where k and l are integers. Proper selection of fc ensures harmonics are pushed to higher frequencies, making them easier to filter.

Practical Implementation

SPWM is widely used in:

Microcontrollers and dedicated PWM controllers (e.g., TI’s C2000 series, STM32) often include hardware support for SPWM generation, reducing computational overhead.

Limitations and Improvements

While SPWM is effective, it has limitations:

SPWM Waveform Generation Comparison of triangular carrier wave and sinusoidal reference wave, showing their intersection points and resulting PWM signal. Time Amplitude Time Amplitude Time Amplitude SPWM Waveform Generation Triangular Carrier Wave (V_carrier) and Sinusoidal Reference Wave (V_ref) Intersection Points (Switching Instants) Resulting PWM Output V_ref (Sinusoidal) V_carrier (Triangular) Switching Points
Diagram Description: The diagram would show the comparison between the triangular carrier wave and sinusoidal reference wave, and how their intersection points determine the PWM switching instants.

4.2 Space Vector PWM (SVPWM)

Space Vector PWM (SVPWM) is an advanced modulation technique used in three-phase inverters to generate PWM signals that optimize voltage utilization and minimize harmonic distortion. Unlike sinusoidal PWM, SVPWM treats the inverter as a single entity, synthesizing the desired output voltage vector by combining the eight possible switching states of a three-phase inverter.

Mathematical Foundation

The three-phase voltages can be represented as space vectors in the α-β plane using the Clarke transformation:

$$ \begin{bmatrix} V_\alpha \\ V_\beta \end{bmatrix} = \frac{2}{3} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} V_a \\ V_b \\ V_c \end{bmatrix} $$

This transformation converts the three-phase quantities into a two-dimensional orthogonal reference frame. The resulting space vector Vref is synthesized using the adjacent active vectors and zero vectors.

Switching States and Voltage Vectors

A three-phase inverter has eight possible switching states (six active and two zero), each corresponding to a unique voltage vector in the α-β plane:

The reference vector Vref is approximated by switching between the two nearest active vectors and zero vectors over a PWM period.

Duty Cycle Calculation

The dwell times for the active vectors are calculated based on the sector in which Vref lies. For a reference vector in Sector 1:

$$ T_1 = \frac{\sqrt{3} T_s}{V_{dc}} |V_{ref}| \sin(60° - \theta) \\ T_2 = \frac{\sqrt{3} T_s}{V_{dc}} |V_{ref}| \sin(\theta) \\ T_0 = T_s - (T_1 + T_2) $$

where Ts is the switching period, Vdc is the DC bus voltage, and θ is the angle of Vref within the sector.

Implementation Steps

  1. Determine the sector: Calculate the angle of Vref and identify the sector (1 to 6).
  2. Compute dwell times: Use the above equations to find T1, T2, and T0.
  3. Generate switching sequence: Apply the active and zero vectors in a symmetric sequence (e.g., V0-V1-V2-V7-V2-V1-V0) to minimize switching losses.

Advantages Over Sinusoidal PWM

Practical Applications

SVPWM is widely used in:

Vref V1 (100) V2 (110) V3 (010) V4 (011) V5 (001) V6 (101)
SVPWM Space Vector Diagram Space vector hexagon with active vectors (V1-V6), zero vectors (V0, V7), and the reference vector Vref in the α-β plane. α β V1 (100) V2 (110) V3 (010) V4 (011) V5 (001) V6 (101) V0/V7 Vref Sector 1
Diagram Description: The diagram would physically show the space vector hexagon with active vectors (V1-V6), zero vectors (V0, V7), and the reference vector Vref in the α-β plane.

Dead-Time Insertion in PWM Signals

Dead-time insertion is a critical technique in PWM-driven power electronics to prevent shoot-through currents in half-bridge or full-bridge configurations. When two complementary PWM signals drive high-side and low-side switches, a finite delay must be introduced between their transitions to ensure one switch is fully off before the other turns on.

Mathematical Basis of Dead-Time Calculation

The required dead time (tdead) depends on the turn-off delay (toff) and turn-on delay (ton) of the power switches (e.g., MOSFETs or IGBTs). For a conservative estimate, the dead time must satisfy:

$$ t_{dead} \geq t_{off,max} - t_{on,min} + t_{margin} $$

where tmargin is an additional safety margin (typically 10-20% of the worst-case delay). For example, if a MOSFET has toff,max = 100 ns and ton,min = 50 ns, with tmargin = 20 ns, the minimum dead time becomes:

$$ t_{dead} \geq 100\,\text{ns} - 50\,\text{ns} + 20\,\text{ns} = 70\,\text{ns} $$

Implementation Methods

Dead-time insertion can be implemented in hardware or software:

$$ t_{dead} = T_{clk} \times DTG $$

where Tclk is the timer clock period.

Impact on PWM Linearity

Dead-time insertion introduces non-linearity in the output voltage, especially at low duty cycles. The effective duty cycle (Deff) deviates from the commanded duty cycle (D) by:

$$ D_{eff} = D - \frac{t_{dead}}{T_{PWM}} \cdot \text{sgn}(I_{load}) $$

where TPWM is the PWM period, and sgn(Iload) accounts for current direction. This distortion is compensated using dead-time compensation algorithms in motor drives and inverters.

Practical Considerations

High-Side PWM Low-Side PWM Dead Time
PWM Dead-Time Timing Diagram A waveform diagram showing the timing relationship between high-side and low-side PWM signals with dead-time intervals clearly marked. Time High Low High-Side PWM Low-Side PWM t_dead t_dead Falling Rising Rising Falling
Diagram Description: The diagram would physically show the timing relationship between high-side and low-side PWM signals with dead-time intervals clearly marked.

5. Noise and EMI Considerations

5.1 Noise and EMI Considerations

Fundamental Noise Mechanisms in PWM

PWM signals inherently generate high-frequency spectral content due to their abrupt transitions between logic levels. The Fourier series representation of an ideal PWM waveform with duty cycle D and period T reveals harmonic components at integer multiples of the switching frequency fsw:

$$ V(t) = V_{DC}D + \sum_{n=1}^{\infty} \frac{2V_{DC}}{n\pi} \sin(n\pi D) \cos(2\pi n f_{sw} t) $$

The harmonic amplitudes follow a sinc function envelope, with nulls occurring at integer multiples of 1/D. Practical implementations exhibit additional spectral contamination from:

EMI Coupling Pathways

PWM-related interference propagates through three primary mechanisms:

Conducted (LISN) Radiated (Antenna) Crosstalk (Near Field)

Conducted emissions dominate below 30MHz, with characteristic impedance mismatches causing standing waves. Radiated emissions peak at frequencies where PCB trace lengths approach λ/4 of harmonic components.

Mitigation Techniques

Time-Domain Strategies

Frequency-Domain Approaches

Spread spectrum techniques modulate fsw with triangular or Hershey-kiss profiles, reducing peak emissions by 10-15dB. The modulation depth Δf should satisfy:

$$ \Delta f > \frac{1}{T_{meas}} $$

where Tmeas is the EMI receiver's integration time.

Layout Considerations

Critical PCB design rules for PWM circuits:

Parameter Recommended Value
Loop area < 4cm2 per amp of switched current
Ground plane cutouts Minimum 3× dielectric thickness from high dv/dt nodes
Via stitching λ/20 spacing at highest harmonic frequency

Differential-mode noise dominates below 1MHz, while common-mode becomes significant at higher frequencies due to parasitic capacitances (typically 2-10pF in power stages).

Filter Design Methodology

A second-order LC filter with damping factor ζ = 0.707 provides optimal attenuation:

$$ f_c = \frac{1}{2\pi\sqrt{LC}} $$ $$ Q = \frac{1}{2}\sqrt{\frac{L}{C}\left(\frac{1}{R_{load}} + \frac{1}{R_{damp}}\right)} $$

Practical implementations often require additional stages for broadband suppression, with ferrite beads effective above 10MHz for impedance matching.

PWM EMI Coupling Pathways A schematic diagram illustrating three EMI coupling pathways from a PWM source: conducted (LISN), radiated (antenna), and crosstalk (near field). PWM Source LISN Conducted Radiated (Antenna) NF Crosstalk (Near Field)
Diagram Description: The section discusses EMI coupling pathways with three distinct mechanisms, which are inherently spatial and benefit from visual representation.

5.2 Heat Dissipation and Power Handling

Thermal Dynamics in PWM-Driven Systems

PWM-driven power electronics, such as MOSFETs and IGBTs, generate heat primarily due to conduction and switching losses. The total power dissipation Pdiss in a switching device can be decomposed into:

$$ P_{diss} = P_{cond} + P_{sw} $$

where Pcond represents conduction losses and Psw accounts for switching losses. Conduction losses arise from the device's on-state resistance RDS(on) and the RMS current IRMS:

$$ P_{cond} = I_{RMS}^2 R_{DS(on)} $$

Switching Losses and Frequency Dependence

Switching losses occur during the transient phases of turn-on and turn-off. For a MOSFET switching at frequency fsw, the energy dissipated per cycle Esw is given by:

$$ E_{sw} = \frac{1}{2} V_{DS} I_D (t_r + t_f) $$

where tr and tf are the rise and fall times, respectively. The total switching power loss scales linearly with frequency:

$$ P_{sw} = E_{sw} f_{sw} $$

Thermal Resistance and Junction Temperature

The device's junction temperature Tj must be kept below its maximum rated value to prevent failure. The thermal path from junction to ambient is characterized by thermal resistance θJA:

$$ T_j = T_a + P_{diss} θ_{JA} $$

where Ta is the ambient temperature. For high-power applications, a heatsink with low thermal resistance θHS is often necessary to maintain safe operating conditions.

Practical Design Considerations

Case Study: Buck Converter Thermal Analysis

Consider a synchronous buck converter with Vin = 24V, Vout = 5V, Iout = 10A, and fsw = 500kHz. Using a MOSFET with RDS(on) = 5mΩ and tr = tf = 20ns, the conduction and switching losses are:

$$ P_{cond} = (10A)^2 \times 5mΩ = 0.5W $$ $$ E_{sw} = \frac{1}{2} \times 24V \times 10A \times 40ns = 4.8μJ $$ $$ P_{sw} = 4.8μJ \times 500kHz = 2.4W $$

For θJA = 40°C/W and Ta = 25°C, the junction temperature reaches:

$$ T_j = 25°C + (0.5W + 2.4W) \times 40°C/W = 141°C $$

This exceeds typical limits (125°C), necessitating a heatsink or reduced switching frequency.

Thermal Resistance Model of PWM Device Thermal schematic showing the path from junction to ambient with labeled thermal resistances (θJC, θCS, θSA) and heat flow arrows. Junction (Tj) Case (Tc) Heatsink (Ths) Ambient (Ta) θJC θCS θSA Pdiss Heat Flow Direction → Thermal Resistance (θ): θJC: Junction-to-Case, θCS: Case-to-Heatsink, θSA: Heatsink-to-Ambient
Diagram Description: The diagram would show the thermal path from junction to ambient with labeled thermal resistances and heat flow arrows.

5.3 Optimization of PWM Parameters for Efficiency

Trade-offs in Duty Cycle and Frequency Selection

The efficiency of a PWM-driven system depends critically on the interplay between duty cycle (D) and switching frequency (fsw). For a resistive load, power dissipation due to switching losses scales quadratically with frequency:

$$ P_{sw} = \frac{1}{2} C V^2 f_{sw} $$

where C is the parasitic capacitance of the switching node. Conversely, conduction losses (Pcond) rise with duty cycle due to I2R effects. The optimal operating point minimizes total losses:

$$ P_{total} = P_{sw} + P_{cond} = \frac{1}{2} C V^2 f_{sw} + I_{rms}^2 R_{ds(on)} D $$

Dead-Time Optimization

In bridge converters, dead time (td) prevents shoot-through but introduces cross-conduction losses. The optimal dead time balances:

For a MOSFET-based H-bridge, the empirical formula for minimum dead time is:

$$ t_{d,min} = t_{off} + \frac{Q_{rr}}{I_{load}} + t_{prop} $$

Harmonic Distortion Mitigation

High-frequency PWM reduces audible noise but increases EMI. The harmonic content of a PWM signal follows a sinc envelope:

$$ H_n = V_{dc} \cdot D \cdot \text{sinc}\left( \frac{n \pi D}{2} \right) $$

where n is the harmonic order. For motor drives, frequencies above 20 kHz avoid audible effects, while RF applications may require spread-spectrum modulation techniques.

Thermal Considerations

Switching devices exhibit a thermal impedance (Zth) that limits maximum fsw. The junction temperature rise is:

$$ \Delta T_j = P_{total} \cdot Z_{th(j-a)} $$

For forced-air cooling, derating curves typically show a 10% efficiency drop per 25°C above 100°C ambient.

Case Study: Buck Converter Optimization

A 12V-to-5V buck converter with L = 10 µH and Coss = 100 pF achieves peak efficiency (94%) at:

PWM Efficiency Optimization Curves A graph showing PWM efficiency optimization curves, including total power loss, switching loss, and conduction loss as functions of switching frequency, with an optimal operating point marked. Switching Frequency (f_sw) Power Loss f1 f_sw(opt) f2 P_total P_sw P_cond Optimal Point D(opt)
Diagram Description: The section discusses complex trade-offs between duty cycle, frequency, and losses, which would benefit from a visual representation of the efficiency curves and loss breakdown.

6. Key Books and Publications on PWM

6.1 Key Books and Publications on PWM

6.2 Online Resources and Tutorials

6.3 Research Papers and Case Studies