RC Circuits

1. Definition and Basic Components

Definition and Basic Components

An RC circuit consists of a resistor (R) and a capacitor (C) connected in series or parallel, forming a first-order linear system governed by differential equations. These circuits exhibit transient behavior when subjected to step inputs, making them fundamental in signal processing, filtering, and timing applications.

Core Components

The two primary elements of an RC circuit are:

Mathematical Foundation

The time-dependent behavior of an RC circuit is derived from Kirchhoff's voltage law (KVL). For a series RC circuit with a voltage source Vs:

$$ V_s = V_R + V_C = IR + \frac{Q}{C} $$

Substituting I = dQ/dt and rearranging yields the first-order differential equation:

$$ \frac{dQ}{dt} + \frac{Q}{RC} = \frac{V_s}{R} $$

The solution for the charging capacitor voltage (VC) is:

$$ V_C(t) = V_s \left(1 - e^{-t/\tau}\right) $$

where Ï„ = RC is the time constant, representing the time required for the voltage to reach ~63.2% of its final value.

Practical Applications

R C V_s GND

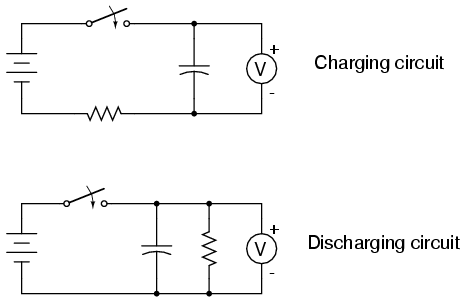
The diagram above illustrates a series RC circuit driven by a voltage source Vs. The resistor and capacitor share the same current, while their voltages add up to the source voltage.

Time Constant (Ï„) and Its Significance

The time constant, denoted by Ï„, is a fundamental parameter in RC circuits that quantifies the rate at which the circuit responds to changes in voltage or current. It is defined as the product of the resistance R and the capacitance C:

$$ \tau = RC $$

Physically, Ï„ represents the time required for the voltage across the capacitor to reach approximately 63.2% of its final value during charging or to decay to 36.8% of its initial value during discharging. This exponential behavior arises from the solution to the first-order differential equation governing RC circuits.

Mathematical Derivation

Consider a simple RC circuit with a voltage source V, resistor R, and capacitor C. Applying Kirchhoff's voltage law during charging yields:

$$ V = iR + \frac{q}{C} $$

Since i = dq/dt, this becomes a first-order differential equation:

$$ \frac{dq}{dt} + \frac{q}{RC} = \frac{V}{R} $$

The solution to this equation gives the charge q(t) as a function of time:

$$ q(t) = CV(1 - e^{-t/\tau}) $$

Differentiating this gives the current:

$$ i(t) = \frac{V}{R}e^{-t/\tau} $$

Practical Significance

The time constant has several critical implications:

Real-World Applications

Time constants are crucial in:

For example, in oscilloscope probes, proper compensation requires matching the probe's time constant (RprobeCprobe) to the oscilloscope input's time constant (RscopeCscope) to prevent waveform distortion.

Multiple Time Constants

While one time constant (1Ï„) reaches ~63% of final value, engineers often consider:

This exponential approach to steady state is characteristic of all first-order systems and appears in thermal, fluid, and other physical systems beyond electronics.

RC Circuit Charging/Discharging Voltage vs. Time A waveform plot showing the exponential charging and discharging voltage curves of a capacitor in an RC circuit, with key time constants (Ï„) and voltage percentages labeled. Time (t) Voltage (V) V_final Ï„ 2Ï„ 3Ï„ 5Ï„ 63.2% 36.8% Charging Discharging
Diagram Description: The diagram would show the exponential charging/discharging voltage curves of the capacitor over time, with key points marked at 1Ï„, 2Ï„, etc.

Charging and Discharging Processes

Transient Response of First-Order RC Circuits

The charging and discharging behavior of an RC circuit follows an exponential transient response governed by Kirchhoff's voltage law and the capacitor's time-dependent charge accumulation. For a series RC circuit with a DC voltage source Vs, resistor R, and capacitor C, the differential equation describing the capacitor voltage VC(t) is:

$$ RC\frac{dV_C}{dt} + V_C = V_s $$

Solving this first-order linear differential equation yields the general solution for charging (initial condition VC(0) = 0):

$$ V_C(t) = V_s(1 - e^{-t/\tau}) $$

where Ï„ = RC is the time constant. The current through the circuit during charging is:

$$ I(t) = \frac{V_s}{R}e^{-t/\tau} $$

Discharge Phase Analysis

When the voltage source is removed and the capacitor discharges through the resistor, the governing equation becomes:

$$ RC\frac{dV_C}{dt} + V_C = 0 $$

With initial condition VC(0) = V0, the solution for discharging is:

$$ V_C(t) = V_0 e^{-t/\tau} $$

The discharge current flows in the opposite direction to the charging current:

$$ I(t) = -\frac{V_0}{R}e^{-t/\tau} $$

Time Constant and Practical Significance

The time constant Ï„ determines how quickly the circuit reaches equilibrium:

In practical applications, this behavior is crucial for:

Non-Ideal Considerations

Real-world RC circuits exhibit additional effects:

The complete transient response must account for these factors in precision timing applications.

R C V_s
RC Circuit Transient Response A diagram showing an RC circuit schematic with voltage and current transient response graphs during charging and discharging phases. V_s R C Ï„ = RC Time (t) V_C(t) Charging Discharging Ï„ 63.2% 36.8% Time (t) I(t) Charging Discharging Ï„ 36.8%
Diagram Description: The diagram would show the exponential voltage/current waveforms during charging and discharging, alongside the RC circuit schematic.

2. Differential Equation Approach

2.1 Differential Equation Approach

The behavior of an RC circuit can be rigorously analyzed using differential equations, providing a mathematical foundation for understanding transient responses. Consider a simple series RC circuit with a resistor R, capacitor C, and voltage source V(t). Applying Kirchhoff’s Voltage Law (KVL) yields:

$$ V(t) = V_R(t) + V_C(t) $$

Substituting Ohm’s Law (V_R = IR) and the capacitor’s voltage-current relationship (I = C dV_C/dt), we obtain:

$$ V(t) = R \cdot C \frac{dV_C}{dt} + V_C(t) $$

This is a first-order linear ordinary differential equation (ODE) in V_C(t). For a constant input voltage V_0, the homogeneous solution describes the transient response, while the particular solution gives the steady-state behavior.

Solving the Homogeneous Equation

For the homogeneous case (V(t) = 0), the equation simplifies to:

$$ \frac{dV_C}{dt} + \frac{1}{RC} V_C = 0 $$

The solution takes the form:

$$ V_C(t) = V_0 e^{-t/\tau} $$

where τ = RC is the time constant, governing the decay rate. This exponential decay characterizes the capacitor’s discharge through the resistor.

Particular Solution and Complete Response

For a DC input V(t) = V_0, the particular solution is simply V_C = V_0. Combining homogeneous and particular solutions, the complete response for a charging capacitor is:

$$ V_C(t) = V_0 \left(1 - e^{-t/\tau}\right) $$

This equation describes the capacitor’s voltage asymptotically approaching V_0 with a time constant τ.

General Solution for Time-Varying Inputs

For arbitrary V(t), the solution is derived using an integrating factor e^{t/Ï„}:

$$ V_C(t) = e^{-t/\tau} \left( \int_0^t \frac{V(t')}{\tau} e^{t'/\tau} dt' + V_C(0) \right) $$

This integral form is particularly useful for analyzing circuits with non-constant inputs, such as pulse or sinusoidal signals.

Practical Implications

The differential equation approach reveals key insights:

Step Response of RC Circuits

The step response of an RC circuit describes how the voltage across the capacitor or the current through the resistor evolves when a sudden step voltage is applied. This behavior is fundamental in signal processing, control systems, and transient analysis.

Mathematical Derivation

Consider a series RC circuit with a resistor R and capacitor C connected to a voltage source V0 via a switch. At t = 0, the switch closes, applying a step input. Kirchhoff’s Voltage Law (KVL) gives:

$$ V_0 = v_R(t) + v_C(t) $$

Since vR(t) = i(t)R and i(t) = C(dvC/dt), the differential equation becomes:

$$ V_0 = RC \frac{dv_C}{dt} + v_C $$

This is a first-order linear differential equation. Solving it with the initial condition vC(0) = 0 yields:

$$ v_C(t) = V_0 \left(1 - e^{-t/\tau}\right) $$

where Ï„ = RC is the time constant. The resistor voltage vR(t) follows from KVL:

$$ v_R(t) = V_0 e^{-t/\tau} $$

Time Constant and Transient Behavior

The time constant Ï„ determines how quickly the circuit reaches steady state:

The step response is characterized by an exponential rise (capacitor) or decay (resistor), critical in timing applications like pulse shaping and delay circuits.

Practical Applications

RC step response is exploited in:

Frequency Domain Interpretation

The step response can also be analyzed using Laplace transforms. The transfer function H(s) of the capacitor voltage is:

$$ H(s) = \frac{v_C(s)}{V_0(s)} = \frac{1}{1 + sRC} $$

Inverse transforming gives the same time-domain solution, reinforcing the duality between time and frequency analysis.

Effect of Non-Ideal Components

Real-world capacitors exhibit parasitic elements like Equivalent Series Resistance (ESR) and inductance, altering the ideal step response. For high-frequency steps, these parasitics cause ringing or overshoot, necessitating careful component selection in high-speed designs.

RC Circuit Step Response A diagram showing an RC circuit schematic with a step input, along with the exponential voltage waveforms across the capacitor and resistor, illustrating the time constant's effect on the transient response. Vâ‚€ R C v_C(t) v_R(t) Time (t) v_C(t) v_R(t) Ï„ 5Ï„ 63.2% Vâ‚€
Diagram Description: The diagram would show the RC circuit schematic with a step input, the exponential voltage waveforms across the capacitor and resistor, and the time constant's effect on the transient response.

Frequency Response and Impedance

The frequency-dependent behavior of an RC circuit is governed by the complex impedance of the capacitor, which varies with the input signal frequency. The impedance Z of a capacitor is given by:

$$ Z_C = \frac{1}{j\omega C} $$

where ω is the angular frequency (ω = 2πf) and C is the capacitance. The resistor's impedance remains constant as Z_R = R, independent of frequency.

Total Impedance of an RC Circuit

For a series RC circuit, the total impedance is the phasor sum of the resistive and capacitive impedances:

$$ Z_{total} = R + \frac{1}{j\omega C} = R - \frac{j}{\omega C} $$

The magnitude of the impedance is:

$$ |Z_{total}| = \sqrt{R^2 + \left(\frac{1}{\omega C}\right)^2} $$

This equation shows that at low frequencies, the capacitive reactance dominates, while at high frequencies, the resistor dominates.

Frequency Response and Cutoff Frequency

The transfer function H(ω) of a series RC circuit (voltage across the capacitor) is:

$$ H(\omega) = \frac{V_C}{V_{in}} = \frac{1/j\omega C}{R + 1/j\omega C} = \frac{1}{1 + j\omega RC} $$

The magnitude of the transfer function is:

$$ |H(\omega)| = \frac{1}{\sqrt{1 + (\omega RC)^2}} $$

The cutoff frequency f_c, where the output power is halved (−3 dB point), occurs when ωRC = 1:

$$ f_c = \frac{1}{2\pi RC} $$

Below f_c, the circuit passes signals with minimal attenuation; above f_c, signals are increasingly attenuated.

Phase Shift in RC Circuits

The phase angle θ between the input and output voltages is:

$$ \theta = -\tan^{-1}(\omega RC) $$

At low frequencies (ω → 0), the phase shift approaches −90° (output lags input). At high frequencies (ω → ∞), the phase shift approaches 0°.

Bode Plot Representation

The frequency response is often visualized using a Bode plot, which consists of:

The slope of the magnitude plot is −20 dB/decade above the cutoff frequency, characteristic of a first-order low-pass filter.

Applications in Filter Design

RC circuits are fundamental in designing:

For example, in audio systems, an RC low-pass filter can suppress high-frequency noise above the audible range, while in communication systems, high-pass RC filters remove DC bias from modulated signals.

Impedance Matching and Power Transfer

In RF circuits, the impedance of an RC network must often match the source or load impedance to maximize power transfer. The condition for maximum power transfer occurs when the load impedance is the complex conjugate of the source impedance.

$$ Z_{load} = Z_{source}^* $$

For an RC circuit driving a resistive load, this requires compensating for the capacitive reactance at the operating frequency.

RC Circuit Frequency Response and Bode Plot A diagram showing an RC circuit schematic with its corresponding Bode magnitude and phase plots, illustrating the frequency response and phase shift characteristics. V_in R C V_out |H(ω)| (dB) Frequency (log) f_c -20 dB/decade -3 dB θ(ω) (°) Frequency (log) f_c -90° to 0° RC Circuit Frequency Response and Bode Plot
Diagram Description: The section discusses frequency response, phase shift, and Bode plots, which are inherently visual concepts requiring graphical representation of magnitude/phase vs. frequency.

3. Filters: Low-Pass and High-Pass

3.1 Filters: Low-Pass and High-Pass

Fundamentals of RC Filters

An RC circuit can function as a frequency-selective filter, either attenuating high frequencies (low-pass) or low frequencies (high-pass). The behavior arises from the frequency-dependent impedance of the capacitor, given by:

$$ Z_C = \frac{1}{j\omega C} $$

At low frequencies, the capacitor's impedance dominates, while at high frequencies, the resistor's impedance becomes significant. The transition between these regimes defines the filter's cutoff frequency.

Low-Pass Filter

In a low-pass configuration, the output is taken across the capacitor. The transfer function H(ω) relates the output voltage to the input voltage:

$$ H(\omega) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j\omega RC} $$

The magnitude of the transfer function is:

$$ |H(\omega)| = \frac{1}{\sqrt{1 + (\omega RC)^2}} $$

The cutoff frequency fc, where the output power is halved (-3 dB point), is:

$$ f_c = \frac{1}{2\pi RC} $$

Below fc, signals pass with minimal attenuation; above fc, they are increasingly suppressed. This behavior is crucial in applications like audio signal processing and anti-aliasing in analog-to-digital converters.

High-Pass Filter

In a high-pass configuration, the output is taken across the resistor. The transfer function is:

$$ H(\omega) = \frac{j\omega RC}{1 + j\omega RC} $$

The magnitude response is:

$$ |H(\omega)| = \frac{\omega RC}{\sqrt{1 + (\omega RC)^2}} $$

The cutoff frequency remains fc = 1/(2Ï€RC), but now frequencies below fc are attenuated, while higher frequencies pass through. High-pass filters are used in AC coupling and noise reduction where DC or low-frequency drift must be removed.

Phase Response

Both filters introduce a phase shift between input and output signals. For the low-pass filter, the phase angle φ is:

$$ \phi = -\tan^{-1}(\omega RC) $$

For the high-pass filter:

$$ \phi = \frac{\pi}{2} - \tan^{-1}(\omega RC) $$

At the cutoff frequency, the phase shift is ±45°. This property is critical in feedback systems where phase margins affect stability.

Practical Considerations

Real-world implementations must account for non-ideal components. Capacitors exhibit equivalent series resistance (ESR), and resistors may have parasitic capacitance. These factors modify the actual cutoff frequency and attenuation characteristics. For precision applications, active filters using operational amplifiers are often preferred over passive RC networks.

Applications

RC Filter Characteristics A diagram showing RC low-pass and high-pass filter circuits, their Bode plots (magnitude and phase), and input/output waveforms. RC Filter Characteristics Low-Pass Filter R C V_in V_out High-Pass Filter C R V_in V_out Magnitude Response 0 dB -3 dB Frequency (log) Gain (dB) f_c Phase Response Frequency (log) -90° 0° +90° -45° +45° Input/Output Waveforms V_in V_out (LPF) V_out (HPF)
Diagram Description: The section describes frequency-dependent behavior and phase shifts that are best visualized with Bode plots and circuit schematics.

3.2 Timing Circuits and Oscillators

Basic RC Timing Circuit

The simplest form of an RC timing circuit consists of a resistor and capacitor in series, driven by a step voltage. The time constant Ï„ governs the exponential charging and discharging of the capacitor:

$$ \tau = RC $$

When a step input Vin is applied, the voltage across the capacitor VC(t) evolves as:

$$ V_C(t) = V_{in} \left(1 - e^{-t/\tau}\right) $$

Conversely, during discharge, the voltage decays as:

$$ V_C(t) = V_0 e^{-t/\tau} $$

where V0 is the initial voltage. These equations form the foundation for pulse generation and delay circuits.

Schmitt Trigger Oscillator

A classic RC oscillator employs a Schmitt trigger inverter to generate square waves. The hysteresis of the Schmitt trigger creates two threshold voltages, VTH (high) and VTL (low). The capacitor charges through R until it reaches VTH, triggering the output to switch low. The capacitor then discharges until it hits VTL, repeating the cycle.

The oscillation period T is derived from the charging and discharging times:

$$ T = \tau \ln \left( \frac{V_{DD} - V_{TL}}{V_{DD} - V_{TH}} \cdot \frac{V_{TH}}{V_{TL}} \right) $$

For symmetric thresholds (VTH = −VTL), this simplifies to:

$$ T = 2\tau \ln \left( \frac{V_{DD} + V_{TH}}{V_{DD} - V_{TH}} \right) $$

Astable Multivibrator

A more precise square-wave oscillator can be built using an astable multivibrator with two transistors. The circuit alternates between two states, with each transistor's conduction period determined by an RC network. The oscillation frequency is:

$$ f = \frac{1}{2R C \ln(2)} \approx \frac{0.72}{RC} $$

This configuration is widely used in clock generation due to its simplicity and reliability.

Phase-Shift Oscillator

For sinusoidal outputs, a phase-shift oscillator employs multiple RC stages to achieve a total phase shift of 180° at the oscillation frequency. The Barkhausen criterion requires:

$$ \beta A = 1 $$

where β is the feedback factor and A is the amplifier gain. For a three-stage RC network, the oscillation frequency is:

$$ f = \frac{1}{2\pi RC \sqrt{6}} $$

and the amplifier must provide a gain of at least 29 to sustain oscillations.

Wien Bridge Oscillator

The Wien bridge oscillator offers improved frequency stability by using a balanced bridge network. The feedback loop consists of a series RC and parallel RC network, producing a phase shift of zero at the resonant frequency:

$$ f = \frac{1}{2\pi RC} $$

The amplifier must have a gain of exactly 3 to maintain oscillations. Automatic gain control (AGC) is often employed to stabilize the output amplitude.

Applications in Real-World Systems

RC Timing Circuit Waveforms A time-domain plot showing step input voltage and capacitor voltage during charge/discharge cycles, with time constant markers and exponential curve annotations. Time (t) V_in V_C(t) V_in 1-e^(-t/Ï„) e^(-t/Ï„) Ï„
Diagram Description: The section involves voltage waveforms and time-domain behavior, which are highly visual concepts.

3.3 Coupling and Bypass Capacitors

Coupling Capacitors

Coupling capacitors are employed in amplifier circuits to block DC components while allowing AC signals to pass. The capacitor forms a high-pass filter with the input impedance of the subsequent stage. The cutoff frequency fc is determined by:

$$ f_c = \frac{1}{2\pi R C} $$

where R is the input resistance of the next stage and C is the coupling capacitance. For minimal signal attenuation, fc should be significantly lower than the lowest frequency of interest. In audio applications, a typical value might be 10 µF for a 1 kΩ load, yielding fc ≈ 16 Hz.

Bypass Capacitors

Bypass capacitors stabilize voltage supplies by providing a low-impedance path to ground for AC signals. They are placed in parallel with emitter or source resistors in amplifier stages to prevent negative feedback from degrading AC gain. The effective impedance Zbypass is given by:

$$ Z_{bypass} = \frac{1}{j\omega C} \parallel R_E $$

At high frequencies, the capacitor dominates, effectively shorting RE. The bypass capacitor must be large enough to maintain low impedance across the signal bandwidth. For example, a 100 µF capacitor provides ~1.6 Ω reactance at 1 kHz.

Practical Considerations

Parasitic inductance and equivalent series resistance (ESR) become critical at high frequencies. Multilayer ceramic capacitors (MLCCs) are preferred for bypass applications due to their low parasitics. For coupling, electrolytic or film capacitors are common, but their tolerance and leakage current must be accounted for in precision circuits.

Real-World Applications

Mathematical Derivation: Optimal Bypass Capacitance

To derive the minimum bypass capacitance Cbypass for a given emitter resistor RE and lowest frequency fmin:

$$ X_C \ll R_E \implies \frac{1}{2\pi f_{min} C} \leq \frac{R_E}{10} $$

Solving for C:

$$ C \geq \frac{10}{2\pi f_{min} R_E} $$

For RE = 1 kΩ and fmin = 20 Hz, C ≥ 80 µF. A standard 100 µF capacitor would suffice.

Coupling and Bypass Capacitor Configurations Schematic diagram illustrating coupling and bypass capacitor configurations in an RC circuit, showing signal paths and component relationships. C_coupling R_input Input Output f_c C_bypass R_E AC ground Z_bypass Coupling and Bypass Capacitor Configurations
Diagram Description: The section describes high-pass filter behavior and parallel impedance relationships that are easier to grasp visually.

4. Component Selection and Tolerance

4.1 Component Selection and Tolerance

Resistor and Capacitor Tolerance Effects

The performance of an RC circuit is critically dependent on the precision of its components. Resistors and capacitors exhibit manufacturing tolerances, typically expressed as a percentage deviation from the nominal value. For instance, a 10 kΩ resistor with ±5% tolerance may range from 9.5 kΩ to 10.5 kΩ. This variation directly impacts the time constant (τ) of the circuit:

$$ \tau = R \times C $$

If both components have asymmetric tolerances (e.g., R = +5%, C = -10%), the worst-case Ï„ deviates by:

$$ \tau_{\text{max}} = (1.05R) \times (0.90C) = 0.945RC $$ $$ \tau_{\text{min}} = (0.95R) \times (1.10C) = 1.045RC $$

For high-precision applications (e.g., filters, oscillators), 1% or 0.1% tolerance components are recommended. Military-grade or metrology circuits may require laser-trimmed resistors and NP0/C0G capacitors with ±0.05% tolerance.

Temperature and Voltage Coefficients

Beyond initial tolerance, component values drift with environmental conditions:

Voltage dependence is particularly pronounced in Class II ceramic capacitors (e.g., X7R), where capacitance can drop 30% at rated voltage. This nonlinearity affects integrators and timing circuits:

$$ C(V) = C_0 \times (1 - \alpha V^2) $$

where α is the voltage coefficient (typically 0.01–0.1 V⁻² for BaTiO₃-based ceramics).

Parasitic Elements

Real components introduce parasitic inductance (ESL) and resistance (ESR). A multilayer ceramic capacitor (MLCC) might have 2 nH ESL and 50 mΩ ESR, forming a parasitic LC network that resonates at:

$$ f_{\text{res}} = \frac{1}{2\pi\sqrt{ESL \times C}} $$

Above this frequency, the capacitor behaves inductively, degrading high-frequency bypassing. Electrolytic capacitors exhibit higher ESR (1–10 Ω), causing power dissipation (I²R losses) in high-current applications.

Statistical Analysis for Production

In mass-produced circuits, Monte Carlo analysis predicts yield by simulating component variations. For a first-order RC filter with 3σ tolerance bounds, the cutoff frequency (f_c) distribution follows:

$$ f_c = \frac{1}{2\pi RC} $$

If R and C are uncorrelated Gaussian variables, the combined standard deviation is:

$$ \sigma_{f_c} = f_c \sqrt{\left(\frac{\sigma_R}{R}\right)^2 + \left(\frac{\sigma_C}{C}\right)^2} $$

This guides the selection of economically viable tolerances while meeting performance specifications. For example, a ±10% f_c tolerance might require ±5% resistors and ±2% capacitors.

Practical Selection Guidelines

4.2 Effects of Parasitic Elements

Parasitic elements in RC circuits—such as stray capacitance, lead inductance, and equivalent series resistance (ESR)—introduce deviations from ideal behavior, particularly at high frequencies or fast switching speeds. These non-ideal components alter the circuit's transient response, frequency characteristics, and power dissipation.

Stray Capacitance

Unintentional capacitance between conductive traces, component leads, or ground planes manifests as parallel parasitic capacitance (Cp). For an RC circuit with nominal capacitance C, the effective capacitance becomes:

$$ C_{\text{eff}} = C + C_p $$

This shifts the circuit's time constant (Ï„ = RC) and corner frequency (f_c = 1/(2Ï€RC)). In high-frequency applications, Cp can dominate, causing unintended filtering or signal integrity issues.

Equivalent Series Resistance (ESR)

Real capacitors exhibit ESR, a parasitic resistance in series with the ideal capacitance. For a step input, the voltage across the capacitor follows:

$$ V_C(t) = V_0 \left(1 - e^{-t/\tau}\right), \quad \tau = (R + R_{\text{ESR}})C $$

ESR also increases power dissipation (P = I²RESR), leading to self-heating and potential thermal runaway in high-current applications.

Lead Inductance

Parasitic inductance (Lp) from component leads or PCB traces forms an unintended RLC network. The impedance becomes frequency-dependent:

$$ Z = R + j\omega L_p + \frac{1}{j\omega C} $$

At frequencies approaching the resonant point (f_r = 1/(2π√(L_pC))), the circuit exhibits peaking or ringing, compromising stability in pulse applications.

Dielectric Absorption

Imperfections in the capacitor's dielectric material cause charge retention, modeled as a parallel RC network. After discharge, a residual voltage reappears:

$$ V_{\text{residual}} = V_0 \cdot k_d \cdot e^{-t/\tau_d} $$

where kd is the dielectric absorption coefficient and Ï„d the relaxation time constant. This effect is critical in sample-and-hold circuits.

Mitigation Strategies

Parasitic Elements in RC Circuits A diagram showing an RC circuit with parasitic elements (Cp, ESR, Lp) alongside frequency response and transient voltage waveform plots. V R C Cp Lp ESR Frequency (Hz) Impedance (Ω) fr Time (s) Voltage (V) Vresidual Parasitic Elements in RC Circuits
Diagram Description: The section discusses parasitic elements altering circuit behavior in ways that are spatial (stray capacitance between traces) and frequency-dependent (impedance/resonance effects), which are best shown visually.

4.3 Measurement Techniques

Time-Domain Analysis

Time-domain measurements of RC circuits involve analyzing the transient response to step or pulse inputs. The voltage across the capacitor VC(t) follows an exponential charging/discharging curve:

$$ V_C(t) = V_0 \left(1 - e^{-t/\tau}\right) \quad \text{(charging)} $$
$$ V_C(t) = V_0 e^{-t/\tau} \quad \text{(discharging)} $$

where Ï„ = RC is the time constant. An oscilloscope is typically used to capture these waveforms. Key measurements include:

Frequency-Domain Analysis

Frequency response measurements reveal the circuit's behavior across different frequencies. A function generator and oscilloscope (or network analyzer) are used to measure:

$$ H(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j2\pi fRC} $$

The cutoff frequency (fc), where the output power is halved (-3 dB), is given by:

$$ f_c = \frac{1}{2\pi RC} $$

Phase shift measurements between input and output signals are also critical, as an RC circuit introduces a phase lag:

$$ \phi(f) = -\tan^{-1}(2\pi fRC) $$

Impedance Spectroscopy

For advanced characterization, impedance spectroscopy measures the complex impedance Z(ω) of the RC network:

$$ Z(\omega) = R + \frac{1}{j\omega C} $$

This technique is particularly useful for evaluating parasitic effects in real-world components. A frequency response analyzer (FRA) or LCR meter is employed to sweep across a wide frequency range, generating Nyquist or Bode plots.

Practical Considerations

Automated Measurement Systems

LabVIEW or Python-based automation (using libraries like PyVISA) can streamline repetitive measurements, enabling parameter sweeps (e.g., varying R or C) and real-time data logging for statistical analysis.

RC Circuit Time and Frequency Domain Responses Diagram showing RC circuit time-domain charging/discharging curves and frequency-domain Bode plots with key points labeled. Time Domain Response V_C(t) Charging V_C(t) Discharging 0 τ Time Frequency Domain Response Magnitude (dB) Phase (ϕ) 0 f_c Frequency -3dB ϕ = -45° Voltage V_C(t) Gain (dB) Phase (°)
Diagram Description: The section describes exponential charging/discharging curves and frequency-domain phase shifts, which are highly visual concepts.

5. Key Textbooks and Papers

5.1 Key Textbooks and Papers

5.2 Online Resources and Tutorials

5.3 Simulation Tools and Labs