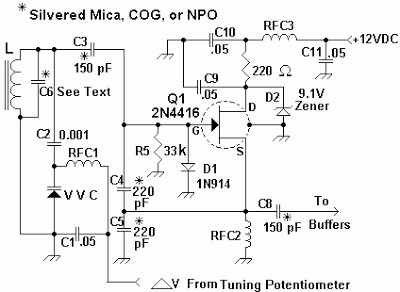
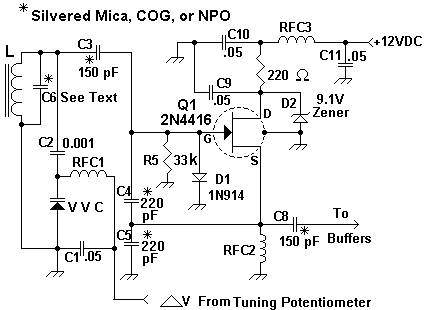
Resonant Circuits

1. Definition and Basic Principles

Resonant Circuits: Definition and Basic Principles

A resonant circuit, also known as a tank circuit, is an electrical network that exhibits resonance at a specific frequency where the inductive and capacitive reactances cancel each other out. This results in a purely resistive impedance, maximizing energy transfer efficiency. Resonant circuits are fundamental in applications such as radio frequency (RF) tuning, filters, oscillators, and impedance matching.

Series and Parallel Resonance

Resonant circuits are broadly classified into two configurations:

Resonant Frequency

The resonant frequency (fr) is determined by the values of inductance (L) and capacitance (C) and is independent of resistance in an ideal circuit. The formula is derived from the condition where inductive reactance (XL) equals capacitive reactance (XC):

$$ X_L = X_C $$ $$ 2\pi f L = \frac{1}{2\pi f C} $$

Solving for f yields the resonant frequency:

$$ f_r = \frac{1}{2\pi \sqrt{LC}} $$

Quality Factor (Q) and Bandwidth

The quality factor (Q) quantifies the sharpness of the resonance peak and is defined as the ratio of stored energy to dissipated energy per cycle:

$$ Q = \frac{f_r}{\Delta f} = \frac{\omega_r L}{R} = \frac{1}{\omega_r C R} $$

where Δf is the bandwidth—the frequency range between the half-power (-3 dB) points. Higher Q indicates lower energy loss and a narrower bandwidth.

Practical Implications

In RF applications, high-Q circuits are essential for selective filtering, while lower-Q circuits are used in broadband systems. The choice between series and parallel resonance depends on whether voltage (parallel) or current (series) amplification is desired.

Impedance vs. Frequency Frequency (Hz) Impedance (Ω) fr
Impedance vs. Frequency in Series and Parallel RLC Circuits A comparison of impedance versus frequency for series and parallel RLC circuits, showing resonant frequency, bandwidth, and impedance characteristics. Frequency (f) Impedance (Z) Series RLC Parallel RLC f_r f_1 f_2 Δf Z_max Z_min X_L = X_C
Diagram Description: The diagram would physically show the impedance vs. frequency relationship for both series and parallel RLC circuits, highlighting the resonant frequency point and bandwidth.

1.2 Resonance Frequency and Conditions

Fundamental Definition of Resonance

Resonance in an electrical circuit occurs when the inductive reactance (XL) and capacitive reactance (XC) cancel each other out, resulting in a purely resistive impedance. At this frequency, the circuit exhibits maximum energy exchange between the inductor and capacitor, with minimal energy dissipation. The resonance condition is mathematically expressed as:

$$ X_L = X_C $$

Substituting the expressions for inductive and capacitive reactance:

$$ \omega L = \frac{1}{\omega C} $$

where ω is the angular frequency in radians per second, L is the inductance in henries, and C is the capacitance in farads.

Derivation of Resonance Frequency

Solving the resonance condition for ω yields the angular resonance frequency:

$$ \omega_0 = \frac{1}{\sqrt{LC}} $$

The standard resonance frequency f0 in hertz is obtained by dividing ω0 by 2π:

$$ f_0 = \frac{1}{2\pi\sqrt{LC}} $$

This equation, known as Thomson's formula, applies to both series and parallel resonant circuits. The frequency f0 represents the point where the circuit's impedance is minimized (series) or maximized (parallel).

Quality Factor and Bandwidth

The sharpness of resonance is quantified by the quality factor Q:

$$ Q = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 CR} $$

For series RLC circuits, Q determines the bandwidth (BW) between the half-power points:

$$ BW = \frac{f_0}{Q} $$

Higher Q values correspond to narrower bandwidths and more selective frequency response, critical in radio receivers and filter design.

Practical Considerations

In real-world applications, component non-idealities affect resonance:

Modern network analyzers measure resonance by sweeping frequency while monitoring impedance phase crossing zero (series) or magnitude peaking (parallel).

Applications in Tuned Circuits

Resonant circuits form the basis of:

In Class C amplifiers, the resonant tank circuit reconstructs the transmitted signal from pulsed collector current, achieving high efficiency at radio frequencies.

Reactance vs Frequency in Resonant Circuit A graph showing the relationship between inductive reactance (X_L), capacitive reactance (X_C), and total reactance as frequency changes, with resonance occurring where X_L and X_C intersect. Frequency (ω) Reactance (X) ω₁ ω₂ ω₀ ω₃ ω₄ X₁ X₂ X₃ 0 -X₁ -X₂ -X₃ Xₗ = ωL X꜀ = 1/ωC Xₜₒₜₐₗ Resonance (ω₀)
Diagram Description: The diagram would show the relationship between inductive and capacitive reactance as frequency changes, and how they cancel at resonance.

1.3 Quality Factor (Q) and Bandwidth

Definition of Quality Factor (Q)

The Quality Factor (Q) quantifies the sharpness of resonance in a resonant circuit. It is defined as the ratio of the energy stored in the system to the energy dissipated per cycle. For a series RLC circuit, Q is expressed as:

$$ Q = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 C R} $$

where ω₀ is the resonant angular frequency, L is inductance, C is capacitance, and R is resistance. A higher Q indicates lower energy loss relative to stored energy, leading to a sharper resonance peak.

Bandwidth and Resonance

The bandwidth (BW) of a resonant circuit is the range of frequencies over which the system's response remains within -3 dB (or 1/√2) of its peak value. For a series RLC circuit, bandwidth is inversely proportional to Q:

$$ BW = \frac{\omega_0}{Q} = \frac{R}{L} $$

This relationship shows that circuits with high Q exhibit narrow bandwidths, making them highly selective to specific frequencies. Conversely, low-Q circuits have broader bandwidths, allowing a wider range of frequencies to pass through.

Practical Implications of Q

In RF and communication systems, high-Q filters are essential for rejecting adjacent channel interference while preserving signal integrity. For example, crystal oscillators leverage high-Q resonators (Q > 10,000) to maintain precise frequency stability. Conversely, audio applications may use low-Q circuits (Q ≈ 0.5–2) to ensure wideband frequency response.

Derivation of Q and Bandwidth Relationship

Starting from the impedance of a series RLC circuit:

$$ Z = R + j\left(\omega L - \frac{1}{\omega C}\right) $$

At resonance, the imaginary component cancels out (ω₀L = 1/ω₀C). The half-power frequencies (ω₁ and ω₂) occur when |Z| = √2R. Solving for these frequencies yields:

$$ \omega_1 = \omega_0 \sqrt{1 + \frac{1}{4Q^2}} - \frac{\omega_0}{2Q} $$ $$ \omega_2 = \omega_0 \sqrt{1 + \frac{1}{4Q^2}} + \frac{\omega_0}{2Q} $$

Subtracting ω₁ from ω₂ gives the bandwidth:

$$ BW = \omega_2 - \omega_1 = \frac{\omega_0}{Q} $$

Parallel RLC Considerations

For a parallel RLC circuit, Q is defined as:

$$ Q = \omega_0 R C = \frac{R}{\omega_0 L} $$

Here, higher parallel resistance R increases Q, reducing bandwidth. This is critical in tank circuits for oscillators, where high Q ensures minimal phase noise.

Experimental Measurement of Q

Q can be measured experimentally using a network analyzer by determining the resonant frequency fâ‚€ and the -3 dB points. The formula simplifies to:

$$ Q = \frac{f_0}{f_2 - f_1} $$

where f₁ and f₂ are the lower and upper half-power frequencies, respectively.

Resonance Curve and Bandwidth for Series RLC Circuit A frequency response curve showing resonant frequency (ω₀), -3 dB points (ω₁, ω₂), bandwidth (BW), and the effect of Q factor on the curve's sharpness. Frequency (ω, logarithmic scale) Normalized Amplitude ω₀ ω₁ ω₂ BW = ω₂ - ω₁ Higher Q = Narrower BW (Dashed: Lower Q) -3 dB
Diagram Description: A diagram would visually show the relationship between Q factor, bandwidth, and the resonance curve's sharpness in a series RLC circuit.

2. Series Resonant Circuits

Series Resonant Circuits

A series resonant circuit consists of an inductor (L), a capacitor (C), and a resistor (R) connected in series with an AC voltage source. At resonance, the inductive and capacitive reactances cancel each other, resulting in a purely resistive impedance.

Impedance and Resonance Frequency

The total impedance Z of a series RLC circuit is given by:

$$ Z = R + j\left(\omega L - \frac{1}{\omega C}\right) $$

where ω is the angular frequency. Resonance occurs when the imaginary part of the impedance vanishes:

$$ \omega L - \frac{1}{\omega C} = 0 $$

Solving for ω, we obtain the resonant frequency fr:

$$ f_r = \frac{1}{2\pi \sqrt{LC}} $$

Quality Factor (Q) and Bandwidth

The quality factor Q measures the sharpness of the resonance peak and is defined as:

$$ Q = \frac{\omega_r L}{R} = \frac{1}{\omega_r C R} $$

At resonance, the voltage across the inductor or capacitor can be much larger than the input voltage, amplified by the factor Q. The bandwidth (BW) of the circuit, defined as the difference between the upper and lower half-power frequencies, is inversely proportional to Q:

$$ BW = \frac{f_r}{Q} $$

Current and Voltage Relationships

At resonance, the current I through the circuit is maximized and in phase with the applied voltage:

$$ I = \frac{V_{in}}{R} $$

The voltages across the inductor and capacitor are equal in magnitude but 180° out of phase, resulting in their cancellation:

$$ V_L = j\omega_r L I $$ $$ V_C = \frac{I}{j\omega_r C} $$ $$ |V_L| = |V_C| = Q V_{in} $$

Practical Applications

Series resonant circuits are widely used in:

Example Calculation

Consider a series RLC circuit with R = 10 Ω, L = 1 mH, and C = 100 nF. The resonant frequency is:

$$ f_r = \frac{1}{2\pi \sqrt{(1 \times 10^{-3})(100 \times 10^{-9})}} \approx 15.92 \text{ kHz} $$

The quality factor Q is:

$$ Q = \frac{\omega_r L}{R} = \frac{2\pi (15.92 \times 10^3)(1 \times 10^{-3})}{10} \approx 10 $$

Thus, the bandwidth is:

$$ BW = \frac{15.92 \text{ kHz}}{10} = 1.592 \text{ kHz} $$
Series RLC Circuit at Resonance A schematic of a series RLC circuit with AC voltage source, resistor (R), inductor (L), and capacitor (C), showing current flow and voltage waveforms at resonance. Vin R L C I Vin I fr: Resonance Frequency VL VC
Diagram Description: The diagram would show the series RLC circuit configuration and the phase relationships between voltage and current at resonance.

2.2 Parallel Resonant Circuits

In a parallel resonant circuit, the inductor and capacitor are connected in parallel across an AC voltage source. Unlike series resonance, where impedance is minimized, parallel resonance maximizes impedance at the resonant frequency, making it a critical concept in filter design, impedance matching, and oscillator circuits.

Impedance Characteristics

The total admittance Y of a parallel RLC circuit is the sum of the individual admittances:

$$ Y = \frac{1}{R} + j \left( \omega C - \frac{1}{\omega L} \right) $$

At resonance, the imaginary component cancels out, reducing the admittance to purely real:

$$ \omega_0 C = \frac{1}{\omega_0 L} $$

Solving for the resonant frequency ω0:

$$ \omega_0 = \frac{1}{\sqrt{LC}} $$

This is identical to the series resonant frequency, but the behavior differs due to the parallel configuration.

Quality Factor (Q) and Bandwidth

The quality factor Q for a parallel resonant circuit is defined as:

$$ Q = R \sqrt{\frac{C}{L}} $$

Higher Q indicates a sharper resonance peak. The bandwidth BW is inversely proportional to Q:

$$ BW = \frac{\omega_0}{Q} $$

In practical applications, high-Q circuits are used in radio receivers to selectively filter desired frequencies while rejecting adjacent channels.

Current and Voltage Relationships

At resonance, the current through the inductor and capacitor can be significantly larger than the source current due to circulating energy:

$$ I_L = I_C = Q \cdot I_{total} $$

This property is exploited in tank circuits, where energy oscillates between the inductor and capacitor with minimal external power input.

Practical Considerations

Real-world inductors have inherent resistance (RL), modifying the parallel resonant impedance:

$$ Z_{res} = \frac{L}{R_L C} $$

Parasitic capacitances and component tolerances further influence performance, necessitating careful design in RF and microwave applications.

AC Source Parallel LC Tank

2.3 Comparison of Series and Parallel Resonance

Resonant circuits exhibit distinct behaviors depending on whether they are configured in series or parallel. While both configurations share the fundamental property of resonance—where inductive and capacitive reactances cancel each other—their impedance, current, and voltage characteristics differ significantly.

Impedance Characteristics

In a series resonant circuit, the impedance at resonance is minimized and purely resistive, given by:

$$ Z_{series} = R $$

This results in a sharp peak in current at the resonant frequency (fr). Conversely, a parallel resonant circuit maximizes impedance at resonance:

$$ Z_{parallel} = \frac{L}{CR} $$

Here, the current through the external supply is minimized, while circulating currents between the inductor and capacitor can be substantial.

Frequency Response and Selectivity

The quality factor (Q) determines the selectivity of the circuit. For series resonance:

$$ Q_{series} = \frac{\omega_r L}{R} = \frac{1}{\omega_r CR} $$

For parallel resonance (with negligible resistance in the inductor):

$$ Q_{parallel} = \omega_r CR = \frac{R}{\omega_r L} $$

Higher Q values lead to sharper resonance peaks and better frequency discrimination, making series circuits ideal for narrowband filtering, while parallel circuits excel in tank applications such as oscillators.

Phase Behavior

Below resonance, a series circuit behaves capacitively (current leads voltage), while above resonance, it behaves inductively (current lags voltage). At resonance, the phase angle is zero. In a parallel circuit:

Practical Applications

Series resonance is employed in:

Parallel resonance finds use in:

Energy Storage and Dissipation

In both configurations, energy oscillates between the inductor and capacitor. However, in series resonance, energy dissipation is dominated by the resistor, while in parallel resonance, the external driving source supplies only the lost energy, making it more efficient for sustained oscillations.

$$ \text{Energy stored} = \frac{1}{2}LI_{max}^2 = \frac{1}{2}CV_{max}^2 $$

where Imax and Vmax are the peak current and voltage, respectively.

Series vs. Parallel Resonance: Impedance & Phase Response Dual-axis Bode plot comparing impedance magnitude and phase response for series and parallel resonant circuits, with annotations for resonant frequency and capacitive/inductive regions. Frequency (f) Low High Series Resonance Z_series Phase fr Capacitive (leading) Inductive (lagging) Parallel Resonance Z_parallel Phase fr Inductive (lagging) Capacitive (leading) 0° (Series) 0° (Parallel) Impedance (Low) Impedance (High)
Diagram Description: The diagram would show side-by-side impedance vs. frequency plots for series and parallel resonance, highlighting their contrasting peaks and phase behaviors.

3. Impedance and Admittance in Resonance

Impedance and Admittance in Resonance

In resonant circuits, the interplay between impedance (Z) and admittance (Y) dictates the system's frequency-dependent behavior. At resonance, the reactive components of impedance cancel out, leading to a purely resistive response. For a series RLC circuit, the impedance is given by:

$$ Z = R + j\left(\omega L - \frac{1}{\omega C}\right) $$

At the resonant frequency ω₀, the imaginary term vanishes, reducing Z to R. This occurs when:

$$ \omega_0 L = \frac{1}{\omega_0 C} \implies \omega_0 = \frac{1}{\sqrt{LC}} $$

Admittance (Y), the reciprocal of impedance, becomes particularly useful in parallel resonant circuits. For a parallel RLC configuration:

$$ Y = \frac{1}{R} + j\left(\omega C - \frac{1}{\omega L}\right) $$

At resonance, the susceptive components cancel, leaving Y = 1/R. The quality factor Q, a measure of energy storage versus dissipation, is derived differently for series and parallel circuits:

Series Resonance

$$ Q_s = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 C R} $$

Parallel Resonance

$$ Q_p = R \omega_0 C = \frac{R}{\omega_0 L} $$

Practical implications include:

In real-world applications, parasitic resistances (e.g., inductor ESR) modify idealized equations. For instance, a practical parallel LC tank circuit's impedance peaks at:

$$ Z_{\text{max}} = Q^2 R $$

where R accounts for all loss mechanisms. This principle underpins oscillator design and impedance-matching networks in wireless systems.

Impedance/Admittance vs Frequency in Resonant Circuits Bode plot showing the impedance and admittance frequency response curves for series and parallel RLC circuits, with resonant frequency, bandwidth, and phase angle markers. Frequency (ω) ω₁ ω₀ ω₂ Magnitude (log) 10⁻² 10⁰ 10² Phase (degrees) -90° 0° +90° Series |Z| Parallel |Y| Phase Q Δω
Diagram Description: The diagram would show the impedance/admittance frequency response curves for series and parallel RLC circuits, illustrating the resonant peak/dip and phase transitions.

3.2 Voltage and Current Characteristics

Voltage and Current in Series RLC Circuits

In a series RLC circuit at resonance, the impedance is minimized and purely resistive, given by Z = R. The current through the circuit reaches its maximum value, Imax = Vin/R, where Vin is the input voltage. The voltage across the inductor (VL) and capacitor (VC) are equal in magnitude but 180° out of phase, resulting in their cancellation. However, individually, they can be significantly larger than the input voltage, a phenomenon known as voltage magnification.

$$ V_L = I \cdot X_L = \frac{V_{in}}{R} \cdot \omega_0 L $$ $$ V_C = I \cdot X_C = \frac{V_{in}}{R} \cdot \frac{1}{\omega_0 C} $$

At resonance (ω = ω0), XL = XC, leading to:

$$ V_L = V_C = Q \cdot V_{in} $$

where Q is the quality factor of the circuit, defined as:

$$ Q = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 C R} $$

Voltage and Current in Parallel RLC Circuits

In a parallel RLC circuit at resonance, the admittance is minimized and purely conductive, given by Y = 1/R. The voltage across the circuit reaches its maximum value, Vmax = Iin R, where Iin is the input current. The currents through the inductor (IL) and capacitor (IC) are equal in magnitude but 180° out of phase, resulting in their cancellation. However, individually, they can be significantly larger than the input current, a phenomenon known as current magnification.

$$ I_L = \frac{V}{X_L} = I_{in} \cdot \frac{R}{\omega_0 L} $$ $$ I_C = \frac{V}{X_C} = I_{in} \cdot \omega_0 C R $$

At resonance (ω = ω0), XL = XC, leading to:

$$ I_L = I_C = Q \cdot I_{in} $$

where Q is the quality factor of the circuit, defined as:

$$ Q = \frac{R}{\omega_0 L} = \omega_0 C R $$

Phase Relationships

The phase difference between voltage and current in a resonant circuit depends on the frequency relative to the resonant frequency:

Practical Implications

The voltage and current magnification effects in resonant circuits are exploited in applications such as:

Understanding these characteristics is critical for designing circuits with desired frequency responses and avoiding excessive voltage or current stresses on components.

Series and Parallel RLC Resonance Characteristics A comparison of series and parallel RLC circuits, showing voltage/current waveforms, phasor diagrams, and resonance frequency markers. Series RLC Circuit Parallel RLC Circuit R L C V = V_R + V_L + V_C R L C I = I_R + I_L + I_C V I ω₀ V I ω₀ V_R V_L V_C Current Reference (I) I_R I_L I_C Voltage Reference (V) Q = V_L/V = V_C/V Q = I_C/I = I_L/I
Diagram Description: The section describes phase relationships and voltage/current magnification, which are highly visual concepts involving waveforms and vector relationships.

3.3 Phase Relationships at Resonance

In a resonant circuit, the phase relationship between voltage and current is a critical indicator of the system's behavior. At resonance, the reactive components—inductive and capacitive—cancel each other, resulting in a purely resistive impedance. This condition leads to distinct phase characteristics that are fundamental in applications like filters, oscillators, and impedance matching networks.

Impedance Phase Angle

The phase angle θ of the total impedance Z in a series RLC circuit is given by:

$$ \theta = \arctan\left(\frac{X_L - X_C}{R}\right) $$

where XL is the inductive reactance, XC is the capacitive reactance, and R is the resistance. At resonance, XL = XC, reducing the phase angle to zero:

$$ \theta = 0 $$

This signifies that the voltage and current are in phase, a defining feature of resonance.

Voltage and Current Phase Shift

Below resonance (f < fr), the capacitive reactance dominates (XC > XL), causing the current to lead the voltage by up to 90°. Above resonance (f > fr), the inductive reactance dominates (XL > XC), leading to a current lag of up to 90°. The transition through resonance is abrupt in high-Q circuits, making phase analysis crucial for tuning.

Practical Implications

Phase relationships are exploited in:

Graphical Representation

The phase response of a resonant circuit can be visualized as a function of frequency. At fr, the phase crosses zero, with steep transitions in high-Q systems. The sharpness of this transition is directly proportional to the circuit's quality factor Q.

Frequency (Hz) 0° -90° +90° Phase Response Near Resonance

Mathematical Derivation of Phase Shift

The transfer function H(f) of a series RLC circuit is:

$$ H(f) = \frac{V_{out}}{V_{in}} = \frac{R}{R + j\left(\omega L - \frac{1}{\omega C}\right)} $$

The phase φ of H(f) is:

$$ \phi = -\arctan\left(\frac{\omega L - \frac{1}{\omega C}}{R}\right) $$

At resonance (ω = ω0), the imaginary term vanishes, yielding φ = 0.

4. Tuning Circuits in Radio Frequency (RF) Systems

4.1 Tuning Circuits in Radio Frequency (RF) Systems

Resonant circuits form the backbone of RF tuning systems, enabling precise frequency selection in communication devices, radar systems, and signal processing applications. The primary function of a tuning circuit is to select a narrow band of frequencies while rejecting others, achieved through the interplay of inductive (L) and capacitive (C) elements.

Series and Parallel Resonance

The behavior of an LC circuit depends on whether the inductor and capacitor are connected in series or parallel. For a series RLC circuit, the impedance Z is minimized at resonance, while for a parallel RLC circuit, the impedance is maximized. The resonant frequency fr is identical in both cases and is given by:

$$ f_r = \frac{1}{2\pi \sqrt{LC}} $$

At resonance, the reactances of the inductor and capacitor cancel each other out, leaving only the resistive component. The quality factor Q quantifies the sharpness of the resonance peak and is defined as:

$$ Q = \frac{\omega_r L}{R} = \frac{1}{\omega_r C R} $$

where ωr is the angular resonant frequency and R is the equivalent series resistance. Higher Q values correspond to narrower bandwidths and more selective tuning.

Practical Tuning Considerations

In real-world RF systems, parasitic elements such as stray capacitance and lead inductance can shift the resonant frequency. To compensate, variable capacitors or inductors are often employed for fine-tuning. The tuning range is determined by the ratio of maximum to minimum capacitance or inductance:

$$ \text{Tuning Ratio} = \frac{C_{max}}{C_{min}} \quad \text{or} \quad \frac{L_{max}}{L_{min}} $$

Modern RF systems frequently use varactor diodes for electronic tuning, where the capacitance is voltage-controlled. The tuning sensitivity, defined as the change in frequency per unit change in control voltage, is a critical parameter:

$$ S = \frac{\partial f_r}{\partial V} $$

Impedance Matching in RF Tuning

Maximum power transfer in RF systems requires impedance matching between stages. The L-network, consisting of two reactive elements, is the simplest matching topology. For a load impedance ZL to be matched to a source impedance ZS, the component values are calculated as:

$$ X_1 = \sqrt{R_S(R_L - R_S)} - X_L $$ $$ X_2 = \frac{R_S R_L}{X_1} $$

where X1 and X2 are the reactances of the matching elements. More complex matching networks like π or T configurations provide broader bandwidth and better harmonic rejection.

Temperature and Stability Effects

Component values drift with temperature, affecting tuning stability. The temperature coefficient of frequency (TCF) quantifies this effect:

$$ TCF = \frac{1}{f_r} \frac{\partial f_r}{\partial T} $$

Compensation techniques include using materials with opposite temperature coefficients or active temperature control. In critical applications, oven-controlled crystal oscillators (OCXOs) maintain frequency stability within parts per million (ppm) over wide temperature ranges.

Phase Noise Considerations

In oscillator circuits, phase noise degrades signal purity and is particularly critical in RF systems. The Leeson model describes phase noise L(fm) as:

$$ L(f_m) = 10 \log \left[ \frac{2FkT}{P_{sig}} \left(1 + \frac{f_0^2}{4Q^2 f_m^2}\right) \left(1 + \frac{f_c}{f_m}\right) \right] $$

where fm is the offset frequency, F is the noise figure, f0 is the carrier frequency, and fc is the flicker noise corner frequency. High-Q resonators and low-noise active devices minimize phase noise.

Advanced Tuning Techniques

Modern RF systems employ digital tuning methods where microcontrollers or DSPs adjust component values via digital-to-analog converters (DACs). Automatic frequency control (AFC) loops maintain lock to a reference signal, while phase-locked loops (PLLs) provide precise frequency synthesis. The loop bandwidth of a PLL must be carefully chosen to balance acquisition speed and noise rejection:

$$ \omega_n = \sqrt{\frac{K_v K_{\phi}}{N}} $$

where Kv is the VCO gain, Kφ is the phase detector gain, and N is the divider ratio. Fractional-N synthesis allows for finer frequency resolution by dynamically changing the division ratio.

Series vs. Parallel RLC Resonance A side-by-side comparison of series and parallel RLC circuits with their corresponding impedance-frequency response curves. Labels include Z_min (series), Z_max (parallel), f_r (resonant frequency), and component values (L, C, R). R L C V Series RLC R L C V Parallel RLC Z f Z_min f_r Z f Z_max f_r
Diagram Description: A diagram would visually contrast series vs. parallel RLC circuits and their impedance behaviors at resonance, which is a spatial concept.

4.2 Filter Design and Signal Processing

Fundamentals of Resonant Filters

Resonant circuits form the backbone of frequency-selective filters, enabling precise control over signal bandwidth and attenuation. The quality factor (Q) determines the sharpness of the filter's frequency response, where a higher Q corresponds to a narrower bandwidth. For a series RLC circuit, the transfer function H(ω) is derived from the impedance ratio:

$$ H(\omega) = \frac{V_{out}}{V_{in}} = \frac{R}{R + j\left(\omega L - \frac{1}{\omega C}\right)} $$

At resonance (ω₀ = 1/√(LC)), the impedance is purely resistive, and the output voltage peaks. The -3 dB bandwidth (Δω) relates to Q via:

$$ Q = \frac{\omega_0}{\Delta\omega} $$

Bandpass and Bandstop Configurations

Bandpass filters (BPF) and bandstop filters (BSF) exploit resonance to either pass or reject a specific frequency range. A parallel RLC circuit acts as a BPF when the output is taken across the tank, while a series RLC with a parallel output functions as a BSF. The normalized magnitude response for a BPF is:

$$ \left| H(\omega) \right| = \frac{1}{\sqrt{1 + Q^2\left(\frac{\omega}{\omega_0} - \frac{\omega_0}{\omega}\right)^2}} $$

For a BSF, the response inverts, with nulls at ω₀. Practical implementations often use active components (e.g., op-amps) to overcome losses in passive designs.

Practical Design Considerations

Component non-idealities—such as parasitic capacitance in inductors or equivalent series resistance (ESR) in capacitors—degrade filter performance. For instance, inductor self-resonance frequency (SRF) limits the usable range of a filter. Advanced techniques include:

Applications in Signal Processing

Resonant filters are pivotal in:

Mathematical Optimization

For a maximally flat passband (Butterworth response), the filter order n is determined by:

$$ n \geq \frac{\log\left(\frac{10^{A_s/10} - 1}{10^{A_p/10} - 1}\right)}{2 \log\left(\frac{\omega_s}{\omega_p}\right)} $$

where Ap and As are passband ripple and stopband attenuation (dB), and ωp, ωs are the edge frequencies.

Frequency Response of a Bandpass Filter ω1 ω2 Q = 5
Bandpass and Bandstop Filter Frequency Responses Side-by-side plots of Bandpass Filter (BPF) and Bandstop Filter (BSF) frequency response curves, showing resonant frequency (ω₀), bandwidth (Δω), and -3 dB points. Frequency (ω) |H(ω)| ω₀ -3 dB -3 dB Δω Q = ω₀/Δω Bandpass Filter (BPF) Bandstop Filter (BSF)
Diagram Description: The section discusses frequency response curves and filter configurations, which are inherently visual concepts.

4.3 Energy Storage and Power Transfer

In resonant circuits, energy oscillates between the inductive and capacitive elements, with minimal dissipation in an ideal lossless system. The instantaneous energy stored in the inductor and capacitor can be expressed as:

$$ W_L(t) = \frac{1}{2} L i^2(t) $$
$$ W_C(t) = \frac{1}{2} C v^2(t) $$

At resonance, the total energy Wtotal remains constant, with the energy shifting between magnetic (inductor) and electric (capacitor) forms. The phase relationship between current and voltage ensures that when WL is maximal, WC is zero, and vice versa.

Quality Factor and Energy Storage

The quality factor Q quantifies the efficiency of energy storage relative to energy loss per cycle. For a series RLC circuit:

$$ Q = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 C R} $$

where ω0 is the resonant frequency. Higher Q indicates lower energy loss, making the circuit more selective. The stored energy ratio to dissipated energy per radian is:

$$ Q = 2\pi \frac{\text{Energy Stored}}{\text{Energy Dissipated per Cycle}} $$

Power Transfer in Resonant Systems

In practical applications, resonant circuits often couple energy between source and load. The maximum power transfer occurs at resonance when the impedance is purely resistive. The power delivered to the load RL in a series RLC circuit is:

$$ P_{avg} = \frac{1}{2} I_{rms}^2 R_L $$

where Irms is the root-mean-square current. For parallel RLC circuits, admittance matching is critical for optimal power transfer.

Practical Considerations

Non-ideal components introduce losses, reducing the effective Q. Parasitic resistances in inductors (RL) and capacitors (RC) must be accounted for:

$$ Q_{actual} = \frac{Q_L Q_C}{Q_L + Q_C} $$

where QL = ωL/RL and QC = 1/(ωCRC). High-frequency applications often use superconducting or low-loss dielectric materials to minimize energy dissipation.

Applications in Wireless Power Transfer

Resonant coupling enables efficient wireless power transfer in systems like inductive charging pads and biomedical implants. The mutual inductance M between coils and their individual Q factors determine the efficiency:

$$ \eta = \frac{k^2 Q_1 Q_2}{1 + k^2 Q_1 Q_2} $$

where k is the coupling coefficient. Optimizing Q and k is essential for achieving high efficiency over varying distances.

Energy Oscillation in Resonant Circuit A diagram showing a parallel LC resonant circuit with energy oscillation between inductor and capacitor, and the phase relationship between current and voltage. L C t W_L(t) W_C(t) i(t) v(t) π/2 π/2
Diagram Description: A diagram would visually demonstrate the oscillation of energy between inductor and capacitor, and the phase relationship between current and voltage at resonance.

5. Component Selection and Tolerance Effects

5.1 Component Selection and Tolerance Effects

The performance of a resonant circuit is critically dependent on the choice of components—primarily inductors (L) and capacitors (C)—and their tolerance specifications. Even minor deviations from nominal values can significantly alter the resonant frequency (fr), quality factor (Q), and bandwidth (BW).

Impact of Component Tolerances on Resonant Frequency

The resonant frequency of an LC circuit is given by:

$$ f_r = \frac{1}{2\pi \sqrt{LC}} $$

If the actual values of L and C deviate from their nominal values due to manufacturing tolerances, the resonant frequency shifts. For small variations, the relative change in fr can be approximated using a first-order Taylor expansion:

$$ \frac{\Delta f_r}{f_r} \approx -\frac{1}{2} \left( \frac{\Delta L}{L} + \frac{\Delta C}{C} \right) $$

For example, a 5% tolerance in both L and C can lead to a worst-case frequency deviation of up to 5%.

Quality Factor Sensitivity to Component Imperfections

The quality factor Q of a series RLC circuit is defined as:

$$ Q = \frac{1}{R} \sqrt{\frac{L}{C}} $$

Component tolerances affect Q in two ways:

Practical Guidelines for Component Selection

To minimize tolerance-induced performance variations:

Case Study: Filter Design with 10% Tolerance Components

Consider a bandpass filter with a target center frequency of 1 MHz. If L and C have 10% tolerances, the actual resonant frequency may vary between 909 kHz and 1.1 MHz. To mitigate this, either:

Mathematical Derivation of Worst-Case Frequency Deviation

For a given tolerance δ (e.g., δ = 0.05 for 5%), the worst-case fractional deviation in fr is:

$$ \left| \frac{\Delta f_r}{f_r} \right|_{\text{max}} = \frac{1}{2} \left( \delta_L + \delta_C \right) $$

where δL and δC are the tolerances of the inductor and capacitor, respectively.

5.2 Losses and Damping in Real Circuits

In an ideal resonant circuit, energy oscillates indefinitely between the inductor and capacitor without dissipation. However, real circuits exhibit losses due to resistive elements, leading to damping. The primary sources of loss include:

Quality Factor (Q) and Damping

The quality factor Q quantifies energy loss relative to stored energy per cycle. For a series RLC circuit:

$$ Q = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 C R} $$

where ω0 is the resonant frequency. Higher Q indicates lower damping. The damping ratio ζ relates to Q as:

$$ \zeta = \frac{1}{2Q} $$

Critical damping occurs when ζ = 1, corresponding to Q = 0.5. Underdamped systems (ζ < 1) exhibit oscillatory decay, while overdamped systems (ζ > 1) decay monotonically.

Equivalent Series Resistance (ESR)

Real capacitors and inductors exhibit frequency-dependent equivalent series resistance (ESR). For a capacitor:

$$ \text{ESR} = \frac{\tan \delta}{\omega C} $$

where tan δ is the loss tangent of the dielectric. Similarly, inductor ESR includes both DC resistance and skin/proximity effect losses at high frequencies.

Loaded Q Factor

When a resonant circuit couples to external loads, the loaded quality factor QL becomes:

$$ \frac{1}{Q_L} = \frac{1}{Q_0} + \frac{1}{Q_{ext}} $$

where Q0 is the unloaded Q and Qext accounts for external loading. This relationship governs bandwidth in filter design and impedance matching networks.

Time-Domain Behavior

The envelope of damped oscillations follows:

$$ V(t) = V_0 e^{-\alpha t} \cos(\omega_d t) $$

where the damping coefficient α = R/2L and the damped frequency ωd = √(ω02 - α2). This exponential decay characterizes energy dissipation mechanisms.

Practical Implications

In RF systems, losses directly impact:

Material selection (e.g., low-loss ceramics for capacitors, Litz wire for inductors) and cryogenic cooling can mitigate losses in high-performance applications.

Damped Oscillation Waveform A time-domain waveform showing a damped oscillation with an exponential decay envelope, labeled with key parameters such as V₀, damping coefficient (α), damped frequency (ω_d), and time (t). t V(t) V₀e^(-αt) ω_d = 2πf_d α V₀
Diagram Description: The section discusses damped oscillations and time-domain behavior, which are best visualized with waveforms showing exponential decay and frequency relationships.

5.3 Simulation and Measurement Techniques

Numerical Simulation of Resonant Circuits

Modern circuit simulation tools, such as SPICE-based software (LTspice, Ngspice, or Cadence PSpice), enable precise modeling of resonant circuits. The key parameters—resonant frequency (fr), quality factor (Q), and bandwidth (BW)—are derived from frequency-domain analysis (AC sweep). The transfer function of a series RLC circuit is given by:

$$ H(j\omega) = \frac{V_{out}}{V_{in}} = \frac{R}{R + j\left(\omega L - \frac{1}{\omega C}\right)} $$

For parallel RLC circuits, the admittance formulation is preferred:

$$ Y(j\omega) = \frac{1}{R} + j\left(\omega C - \frac{1}{\omega L}\right) $$

Transient simulations reveal the step response and damping characteristics, critical for assessing stability in oscillators or filters.

Network Analyzer Measurements

Vector network analyzers (VNAs) provide the most accurate empirical data for resonant circuits. Scattering parameters (S11, S21) quantify reflection and transmission:

$$ S_{21}(f) = 20 \log_{10} \left| \frac{V_{out}(f)}{V_{in}(f)} \right| $$

Calibration (SOLT or TRL) eliminates systematic errors. The Q factor is extracted from the 3-dB bandwidth or phase-slope method:

$$ Q = \frac{f_r}{\Delta f_{-3dB}} = \frac{f_r}{2} \left| \frac{d\phi}{df} \right|_{f=f_r} $$

Impedance Analyzers and Resonance Tracking

Impedance analyzers (e.g., Keysight E4990A) directly measure Z(ω) and θ(ω) using auto-balancing bridges. For high-Q systems (>100), phase-locked loops (PLLs) or null detectors improve accuracy by tracking the zero-reactance frequency (XL = XC).

Time-Domain Reflectometry (TDR)

TDR techniques resolve parasitic effects in PCB-based resonators. The propagation delay (Ï„d) and characteristic impedance (Z0) are derived from reflected waveforms:

$$ Z_0 = \frac{V_{incident}}{I_{incident}} = \sqrt{\frac{L}{C}} $$

where L and C are distributed parameters per unit length.

Nonlinear Resonance Characterization

For circuits with nonlinear components (e.g., ferrite-core inductors), harmonic balance analysis or envelope simulation captures amplitude-dependent frequency shifts. The Duffing equation models such behavior:

$$ \frac{d^2x}{dt^2} + 2\zeta\omega_0 \frac{dx}{dt} + \omega_0^2 x + \epsilon x^3 = F(t) $$

where ε quantifies nonlinear stiffness.

Frequency Response (Magnitude) Frequency (Hz) |H(f)|

Practical Considerations

Resonant Circuit Frequency and Time Domain Responses A three-panel diagram showing magnitude vs. frequency, phase vs. frequency, and transient step response of a resonant circuit. Magnitude Response (dB vs Hz) Phase Response (Degrees vs Hz) Step Response (Voltage vs Time) dB Degrees Voltage f₁ fᵣ f₂ Time fᵣ -3dB -3dB fᵣ Q Overshoot ζ
Diagram Description: The section includes complex frequency-domain and time-domain relationships that are best visualized with labeled waveforms and circuit responses.

6. Key Textbooks and Papers

6.1 Key Textbooks and Papers

6.2 Online Resources and Tutorials

6.3 Advanced Topics for Further Study