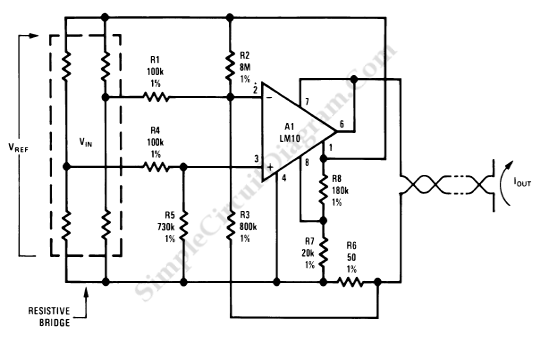
Sensors and Transducers

1. Definition and Key Differences

1.1 Definition and Key Differences

Fundamental Definitions

A sensor is a device that detects and responds to a physical stimulus—such as thermal, mechanical, electrical, or optical input—and converts it into a measurable signal. The output is typically an electrical quantity (voltage, current, resistance) proportional to the input stimulus. For example, a thermocouple generates a voltage in response to temperature gradients via the Seebeck effect:

$$ V_{out} = \alpha (T_1 - T_2) $$

where α is the Seebeck coefficient and T1, T2 are junction temperatures.

A transducer, however, is a broader term encompassing any device that converts energy from one form to another. While all sensors are transducers, not all transducers are sensors. For instance, a loudspeaker is a transducer (electrical to acoustic energy) but not a sensor, as it doesn’t measure input stimuli.

Functional Distinctions

The core difference lies in their operational roles:

Performance Metrics

Sensors are characterized by parameters such as:

Transducers prioritize energy conversion efficiency (η), defined as:

$$ \eta = \frac{P_{out}}{P_{in}} \times 100\% $$

where Pin and Pout are input and output power, respectively.

Practical Implications

In industrial automation, a pressure sensor (e.g., strain-gauge-based) measures hydraulic pressure with high accuracy, while a solenoid valve (transducer) converts electrical signals into mechanical motion to control flow. The former is part of a feedback loop; the latter executes control actions.

Energy Domain Conversion in Transducers Electrical Mechanical

1.2 Basic Working Principles

Energy Conversion Mechanisms

Sensors and transducers operate on the fundamental principle of energy domain conversion, where a physical quantity (mechanical, thermal, electromagnetic, etc.) is transformed into an electrical signal. The transduction mechanism depends on the underlying physical effect being utilized. For instance, piezoelectric sensors convert mechanical strain into charge separation, while thermocouples exploit the Seebeck effect to generate voltage from temperature gradients.

Mathematical Modeling of Transducers

The input-output relationship of a transducer can be described by its transfer function. Consider a generalized first-order linear transducer model:

$$ V_{out}(t) = K \cdot \frac{\tau \frac{dX_{in}(t)}{dt} + X_{in}(t)}{\tau s + 1} $$

where K is the static sensitivity, Ï„ is the time constant, and Xin(t) represents the input physical quantity. This differential equation captures both the steady-state and dynamic response characteristics.

Noise and Resolution Limits

The minimum detectable signal is constrained by various noise sources:

where kB is Boltzmann's constant, T is temperature, R is resistance, q is electron charge, and Δf is bandwidth.

Practical Design Considerations

Key parameters in transducer selection include:

Case Study: MEMS Accelerometer

Modern microelectromechanical (MEMS) accelerometers employ capacitive sensing of a proof mass displacement. The governing equation for such devices is:

$$ C(x) = \frac{\epsilon_0 A}{d_0 \pm x} $$

where ε0 is permittivity, A is plate area, d0 is nominal gap, and x is displacement. The capacitance change is typically measured using a differential bridge circuit or switched-capacitor techniques.

Advanced Sensing Techniques

Recent developments include:

1.3 Classification by Measured Quantity

Sensors and transducers can be systematically categorized based on the physical quantity they measure. This classification is fundamental in selecting the appropriate sensor for a given application, as each type exhibits distinct operating principles, sensitivity ranges, and output characteristics.

Mechanical Quantities

Sensors measuring mechanical quantities respond to changes in position, force, pressure, or motion. Strain gauges, for instance, operate on the principle of piezoresistance, where mechanical deformation alters electrical resistance. The relationship between strain (ε) and resistance change (ΔR/R) is given by the gauge factor (GF):

$$ \frac{\Delta R}{R} = GF \cdot \epsilon $$

Accelerometers, another key example, measure proper acceleration via piezoelectric or capacitive mechanisms. MEMS-based capacitive accelerometers detect displacement of a proof mass between fixed electrodes, with sensitivity directly proportional to the mass and inversely proportional to the spring constant.

Thermal Quantities

Thermal sensors quantify temperature, heat flux, or thermal conductivity. Thermocouples exploit the Seebeck effect, generating a voltage proportional to the temperature difference between junctions of dissimilar metals. The output voltage V for a type-K thermocouple follows:

$$ V = \sum_{n=0}^{N} c_n (T_{\text{hot}} - T_{\text{cold}})^n $$

where cn are material-specific coefficients. Resistance temperature detectors (RTDs) offer higher precision by tracking the linear resistance-temperature relationship of platinum:

$$ R(T) = R_0 [1 + \alpha (T - T_0)] $$

Electromagnetic Quantities

This category includes sensors for electric/magnetic fields, voltage, and current. Hall effect sensors measure magnetic flux density B by detecting the transverse voltage VH across a current-carrying conductor:

$$ V_H = \frac{I B}{n e t} $$

where n is charge carrier density and t is conductor thickness. Rogowski coils, used for alternating current measurement, output a voltage proportional to the rate of change of current via mutual inductance.

Optical Quantities

Photodetectors convert photon flux into electrical signals through various mechanisms. In photodiodes operating in photovoltaic mode, the open-circuit voltage Voc relates to irradiance E by:

$$ V_{oc} = \frac{n k_B T}{q} \ln\left(\frac{I_{ph}}{I_0} + 1\right) $$

where Iph is the photocurrent and I0 the dark current. Pyroelectric sensors detect changes in infrared radiation through temperature-dependent polarization in crystalline materials.

Chemical Quantities

Chemical sensors employ selective interfaces to detect specific analytes. Amperometric gas sensors measure current from redox reactions at an electrode, with limiting current Ilim following:

$$ I_{lim} = n F A D \frac{C}{\delta} $$

where δ is the diffusion layer thickness and C the analyte concentration. Potentiometric sensors like pH electrodes utilize the Nernst equation for ion activity measurement.

Acoustic Quantities

Ultrasonic transducers convert between sound pressure and electrical signals via piezoelectric materials. The resonant frequency fr of a thickness-mode vibrator is determined by:

$$ f_r = \frac{v}{2d} $$

where v is the speed of sound in the material and d the thickness. Microphones employ capacitive or piezoelectric transduction to capture sound waves across audible frequencies.

2. Temperature Sensors (Thermocouples, RTDs, Thermistors)

2.1 Temperature Sensors (Thermocouples, RTDs, Thermistors)

Thermocouples

Thermocouples operate on the Seebeck effect, where a voltage differential arises due to a temperature gradient between two dissimilar metals. The output voltage V is approximated by:

$$ V = \alpha (T_{\text{hot}} - T_{\text{cold}}) + \beta (T_{\text{hot}}^2 - T_{\text{cold}}^2) $$

Here, α and β are material-dependent coefficients. Type K (Chromel-Alumel) thermocouples, for instance, exhibit a sensitivity of ~41 µV/°C. Nonlinearity corrections are often applied via polynomial approximations (e.g., NIST ITS-90 standards).

Practical challenges include cold junction compensation (CJC), where the reference junction temperature must be measured independently (typically via an IC like the MAX31855). Thermocouples are favored in high-temperature industrial applications (e.g., furnaces, jet engines) due to their ruggedness and wide range (-200°C to +2300°C).

Resistance Temperature Detectors (RTDs)

RTDs rely on the temperature-dependent resistivity of pure metals, typically platinum (Pt100 or Pt1000). The Callendar-Van Dusen equation models resistance R(T):

$$ R(T) = R_0 \left[1 + AT + BT^2 + C(T - 100)T^3\right] $$

For T > 0°C, C = 0. Above 0°C, the simplified linear approximation (R(T) ≈ R0(1 + αT), where α = 0.00385 Ω/Ω/°C for Pt100) suffices for many applications. RTDs achieve ±0.1°C accuracy but require 4-wire Kelvin sensing to eliminate lead resistance errors.

Applications include precision lab instruments and medical devices, where stability and repeatability are critical. Self-heating effects must be mitigated by limiting excitation currents (typically <1 mA).

Thermistors

Thermistors exhibit a highly nonlinear negative (NTC) or positive (PTC) temperature coefficient. The Steinhart-Hart equation models NTC thermistor behavior:

$$ \frac{1}{T} = A + B \ln R + C (\ln R)^3 $$

NTC thermistors offer high sensitivity (~4%/°C) but limited linearity, necessitating lookup tables or piecewise approximations. PTC variants (e.g., barium titanate ceramics) are used for overcurrent protection due to their abrupt resistance rise at a critical temperature.

Common applications include temperature compensation in circuits and battery thermal management. Self-heating and calibration drift are key limitations.

Comparative Analysis

Selection depends on trade-offs between response time, environmental robustness, and signal conditioning complexity. For instance, thermocouples dominate in high-temperature industrial settings, while RTDs are preferred in pharmaceutical calibration.

2.2 Pressure Sensors (Piezoelectric, Capacitive, Strain Gauge)

Piezoelectric Pressure Sensors

Piezoelectric sensors exploit the direct piezoelectric effect, where mechanical stress generates an electric charge. The fundamental relationship is governed by:

$$ Q = d_{ij} \cdot F $$

where Q is the generated charge, dij is the piezoelectric coefficient tensor (typically 2-30 pC/N for quartz), and F is the applied force. The voltage output V across electrodes separated by thickness t is:

$$ V = \frac{Q}{C} = \frac{d_{ij} \cdot F \cdot t}{\epsilon_r \epsilon_0 A} $$

with εr being the relative permittivity and A the electrode area. These sensors excel in dynamic pressure measurements (0.1 Pa to 100 MPa) with bandwidths exceeding 100 kHz, making them ideal for combustion monitoring and shock wave detection.

Capacitive Pressure Sensors

Capacitive designs measure the displacement of a diaphragm through capacitance change. The fundamental parallel-plate capacitance equation:

$$ C = \frac{\epsilon A}{d} $$

becomes pressure-dependent as the gap distance d varies. For a circular diaphragm of radius a and thickness h, the center deflection δ under pressure P is:

$$ \delta = \frac{3(1-\nu^2)a^4P}{16Eh^3} $$

where ν is Poisson's ratio and E is Young's modulus. Modern MEMS implementations achieve 0.01% FS accuracy with differential configurations canceling parasitic capacitances. Applications range from barometric altimeters (10-1200 hPa) to medical ventilators.

Strain Gauge Pressure Sensors

Strain gauges convert mechanical deformation into resistance change via the piezoresistive effect. The gauge factor GF relates strain ε to resistance change:

$$ \frac{\Delta R}{R} = GF \cdot \epsilon $$

For metal foil gauges (GF ≈ 2), the Wheatstone bridge output voltage Vout becomes:

$$ V_{out} = V_{ex} \cdot \frac{GF \cdot \epsilon}{4} $$

Silicon piezoresistors (GF ≈ 100) enable higher sensitivity. Bonded strain gauge sensors dominate industrial applications (0-10,000 psi) with 0.1% nonlinearity, while microfabricated versions serve automotive MAP sensors with integrated temperature compensation.

Comparative Performance

Pressure P δ (Deflection)
Pressure Sensor Operating Principles Cross-sectional schematics of three pressure sensor types: piezoelectric, capacitive, and strain gauge, showing their key operational components and labeled parameters. Piezoelectric Crystal F F +Q -Q d_ij Capacitive Diaphragm δ P C Strain Gauge R1 R2 R3 R4 ΔR/R GF V_out
Diagram Description: The section involves spatial relationships in diaphragm deflection and piezoelectric charge generation that are easier to grasp visually.

Position and Displacement Sensors (LVDT, Encoders, Potentiometers)

Linear Variable Differential Transformer (LVDT)

The Linear Variable Differential Transformer (LVDT) is an inductive transducer that converts linear displacement into an electrical signal. It consists of a primary coil and two secondary coils wound symmetrically around a movable ferromagnetic core. When an AC excitation voltage is applied to the primary, the induced voltages in the secondary coils vary differentially with core displacement.

$$ V_{out} = V_{S1} - V_{S2} = k \cdot x \cdot V_{in} $$

Here, k is the sensitivity factor, x is the core displacement, and Vin is the excitation voltage. The output voltage Vout is linear over a specified range, typically ±5% deviation from ideal linearity. LVDTs offer high resolution (sub-micron), infinite mechanical life (no sliding contacts), and robustness in harsh environments.

Rotary and Linear Encoders

Encoders convert angular or linear motion into digital signals. Incremental encoders generate pulse trains corresponding to displacement, requiring a reference point for absolute position. Absolute encoders provide a unique digital code for each position, eliminating the need for homing.

The resolution of an optical encoder is determined by the number of lines per revolution (LPR) for rotary encoders or lines per unit length for linear encoders. Quadrature encoding (A/B channels phase-shifted by 90°) enables direction detection and four-fold resolution enhancement via edge counting:

$$ \text{Resolution} = \frac{360°}{N \times 4} $$

Where N is the number of lines per revolution. Magnetic and capacitive encoders offer alternatives in high-vibration or contaminated environments where optical encoders may fail.

Potentiometric Sensors

Potentiometers are resistive displacement sensors where a wiper moves along a resistive element, creating a voltage divider. The output voltage Vout is linearly proportional to displacement x:

$$ V_{out} = V_{in} \cdot \frac{R(x)}{R_{total}} $$

Wire-wound potentiometers provide high accuracy (0.1% linearity) but limited resolution due to discrete wire turns. Conductive plastic potentiometers offer continuous resolution (theoretically infinite) but lower temperature stability. Potentiometers exhibit mechanical wear over time, making them unsuitable for high-cycle applications compared to LVDTs or encoders.

Comparative Analysis and Applications

LVDTs dominate in precision industrial metrology (e.g., valve positioning in aerospace) and harsh environments (nuclear, oil/gas) due to their non-contact operation. Encoders are preferred in robotics and CNC machinery for high-speed digital feedback. Potentiometers remain cost-effective solutions in automotive throttle position sensing and consumer electronics where longevity requirements are moderate.

Modern hybrid systems combine technologies; for example, LVDTs with integrated electronics provide ratiometric DC outputs, while smart encoders embed microprocessors for onboard error compensation (eccentricity, thermal drift).

This section provides a rigorous technical breakdown of position/displacement sensors, emphasizing mathematical models, operational principles, and comparative performance characteristics without introductory or concluding fluff. The HTML structure follows strict formatting rules with proper heading hierarchy, mathematical notation, and semantic emphasis.
LVDT Structure & Encoder Quadrature Signals Schematic of an LVDT showing primary and secondary coils with movable core, alongside timing diagram of quadrature encoder signals with 90° phase shift. Primary Coil S1 S2 Core Displacement (x) Time Channel A Channel B 90° Phase Shift LVDT Structure & Encoder Quadrature Signals
Diagram Description: The LVDT's coil arrangement and core movement are spatial concepts that text alone cannot fully convey, and encoder quadrature signals require visual representation of phase relationships.

2.4 Optical Sensors (Photodiodes, Phototransistors, IR Sensors)

Photodiodes: Principles and Operation

A photodiode is a semiconductor device that converts incident light into an electrical current through the photoelectric effect. When photons with sufficient energy strike the diode's depletion region, electron-hole pairs are generated, producing a measurable photocurrent. The responsivity (R) of a photodiode, defined as the ratio of photocurrent (Iph) to incident optical power (Popt), is given by:

$$ R = \frac{I_{ph}}{P_{opt}} = \frac{\eta q \lambda}{hc} $$

where η is the quantum efficiency, q is the electron charge, λ is the wavelength of light, h is Planck's constant, and c is the speed of light. Photodiodes operate in either photovoltaic mode (zero bias) or photoconductive mode (reverse bias), with the latter offering faster response times but higher dark current.

Phototransistors: Gain and Bandwidth Trade-offs

Phototransistors amplify photocurrent through transistor action, providing higher sensitivity than photodiodes at the cost of reduced bandwidth. The current gain (β) of a phototransistor relates the collector current (IC) to the base photocurrent (Iph):

$$ I_C = \beta I_{ph} $$

The frequency response is limited by the Miller capacitance and transit time, with the 3-dB cutoff frequency (f3dB) approximated as:

$$ f_{3dB} \approx \frac{1}{2\pi \tau_{tr}} $$

where Ï„tr is the minority carrier transit time across the base region. Darlington configurations can further increase sensitivity but degrade response speed.

Infrared Sensors: Spectral Considerations

Infrared (IR) sensors exploit the 700 nm to 1 mm wavelength range, with material selection critical for optimal performance. Silicon photodiodes detect up to 1100 nm, while InGaAs extends to 2600 nm. The detectivity (D*), a figure of merit for IR sensors, is expressed as:

$$ D^* = \frac{\sqrt{A \Delta f}}{NEP} $$

where A is the detector area, Δf is the bandwidth, and NEP is the noise-equivalent power. Pyroelectric sensors, which respond to changes in IR flux rather than absolute levels, are used in motion detection with typical responsivities of 104–105 V/W.

Practical Applications and Circuit Implementation

Optical sensors require careful circuit design to mitigate noise. A transimpedance amplifier (TIA) is commonly used for photodiodes, with the feedback resistor (Rf) setting the gain:

$$ V_{out} = -I_{ph} R_f $$

For pulsed IR applications like optical communications, high-speed PIN photodiodes with bandwidths exceeding 1 GHz are employed. In industrial automation, diffuse-reflective IR sensors combine emitters and detectors to measure object proximity, with modulation techniques (e.g., 38 kHz carrier) used to reject ambient light interference.

Photodiode Phototransistor Increasing Gain Decreasing Bandwidth
Optical Sensor Performance Trade-offs and Circuit Implementation Comparative block diagram showing photodiode, phototransistor, and IR sensor with performance curves and transimpedance amplifier circuit. Photodiode R = 0.5 A/W D* = 10¹² Jones Phototransistor β = 100-1000 NEP = 10⁻¹³ W/√Hz IR Sensor λ = 700-1100nm f₃dB = 10kHz Gain Bandwidth Photodiode Phototransistor IR Sensor TIA Circuit Rf = 1MΩ ↑ Gain ↓ Bandwidth ↑ Bandwidth ↓ Gain 400nm 1100nm Spectral Response
Diagram Description: The section covers multiple optical sensor types with trade-offs (gain vs. bandwidth) and practical circuit implementations, which benefit from visual comparison and signal flow representation.

3. Amplification and Filtering

3.1 Amplification and Filtering

Amplification in Sensor Signal Conditioning

Sensor outputs are often weak, ranging from microvolts to millivolts, necessitating amplification before further processing. Operational amplifiers (op-amps) are the cornerstone of signal amplification due to their high input impedance, low output impedance, and configurable gain. The non-inverting amplifier configuration is commonly used for sensor signals:

$$ V_{out} = V_{in} \left(1 + \frac{R_f}{R_g}\right) $$

where Rf is the feedback resistor and Rg is the ground resistor. For strain gauges and thermocouples, instrumentation amplifiers provide superior common-mode rejection (CMRR > 100 dB) by combining three op-amps:

$$ V_{out} = \left(V_2 - V_1\right) \left(1 + \frac{2R_1}{R_g}\right) \frac{R_3}{R_2} $$

Noise Considerations and SNR Optimization

Amplification magnifies both signal and noise, making signal-to-noise ratio (SNR) critical. Thermal noise (Johnson-Nyquist noise) fundamentally limits performance:

$$ V_n = \sqrt{4k_BTR\Delta f} $$

where kB is Boltzmann's constant, T is temperature, and Δf is bandwidth. Practical implementations use:

Active Filter Design for Sensor Systems

Filters remove out-of-band noise while preserving signal integrity. Second-order Sallen-Key filters are prevalent due to their simplicity and stability. The transfer function for a low-pass configuration is:

$$ H(s) = \frac{\omega_0^2}{s^2 + \frac{\omega_0}{Q}s + \omega_0^2} $$

where ω0 is the cutoff frequency and Q is the quality factor. For biosensors and vibration monitoring, switched-capacitor filters provide programmable cutoff frequencies through clock control:

$$ f_c = \frac{f_{clk}}{100} \quad \text{(for typical ratio)} $$

Practical Implementation Challenges

Real-world systems must account for:

Modern solutions integrate programmable gain amplifiers (PGA) and adaptive filters in ASICs, achieving >24-bit effective resolution in MEMS sensor interfaces.

Op-amp Configurations and Filter Circuits Schematic diagram showing non-inverting op-amp, instrumentation amplifier, and Sallen-Key filter circuits with labeled components and signal flow. V_in + - R_f V_out Non-Inverting Op-Amp V_in+ V_in- R_g Diff Amp V_out CMRR Instrumentation Amplifier V_in R C + - R C V_out ω₀ = 1/RC Q = 1/2 Sallen-Key Filter
Diagram Description: The section covers multiple amplifier configurations and filter designs that involve spatial relationships between components and signal transformations.

3.2 Analog-to-Digital Conversion

Analog-to-digital converters (ADCs) are critical in bridging the gap between continuous physical signals and discrete digital systems. The conversion process involves sampling, quantization, and encoding, each contributing to the fidelity and accuracy of the digitized signal.

Sampling Theory and the Nyquist Criterion

The sampling theorem, formulated by Harry Nyquist and later formalized by Claude Shannon, states that a continuous signal must be sampled at a rate at least twice its highest frequency component to avoid aliasing. Mathematically, if a signal has a maximum frequency fmax, the sampling frequency fs must satisfy:

$$ f_s \geq 2f_{max} $$

Violating this criterion leads to aliasing, where higher-frequency components fold back into the sampled spectrum, distorting the signal. Anti-aliasing filters (low-pass filters with a cutoff at fs/2) are typically applied before sampling to mitigate this effect.

Quantization and Resolution

Quantization maps the sampled analog voltage to a discrete digital value. An N-bit ADC divides the input range into 2N discrete levels. The quantization error, defined as the difference between the actual analog value and its digital representation, is bounded by:

$$ \Delta = \frac{V_{ref}}{2^N} $$

where Vref is the ADC's reference voltage. The signal-to-quantization-noise ratio (SQNR) for a full-scale sinusoidal input is given by:

$$ SQNR = 6.02N + 1.76 \text{ dB} $$

Higher-resolution ADCs reduce quantization error but require more precise circuitry and introduce trade-offs in speed and power consumption.

ADC Architectures and Trade-offs

Several ADC architectures exist, each optimized for specific applications:

Practical Considerations

Key non-ideal effects in ADC design include:

Modern ADCs often integrate calibration routines to compensate for these errors, particularly in precision applications such as medical instrumentation and scientific measurement.

Applications in Real-World Systems

ADCs are ubiquitous in:

ADC Sampling, Aliasing, and Quantization A diagram illustrating the ADC sampling process, aliasing effect, and quantization steps with labeled waveforms and frequency spectra. Time Domain Representation Original Signal (f_max) Sampling Rate (f_s) Aliased Signal (f_s/2 < f_max) Frequency Domain Representation f_max 2f_max f_s f_s ± f_max Nyquist Frequency (f_s/2) Quantization Δ (LSB) SQNR = 6.02N + 1.76 dB Time (t) Amplitude Frequency (Hz) Magnitude
Diagram Description: The diagram would show the sampling process, aliasing effect, and quantization steps with labeled waveforms and frequency spectra.

3.3 Noise Reduction Techniques

Noise in sensor systems arises from both intrinsic sources (thermal, shot, flicker noise) and extrinsic interference (EMI, crosstalk, power supply ripple). Effective noise reduction requires a systematic approach combining circuit design, signal processing, and physical layout strategies.

Fundamental Noise Sources

The total noise power spectral density Sn(f) in a sensor system can be expressed as:

$$ S_n(f) = 4kTR + \frac{K_f I^\alpha}{f^\beta} + qI + S_{\text{EMI}}(f) $$

where k is Boltzmann's constant, T is temperature, R is resistance, Kf is the flicker noise coefficient, and q is electron charge. The terms represent thermal, flicker (1/f), shot, and external interference noise respectively.

Shielding and Grounding Techniques

Electromagnetic interference can be mitigated through:

The shielding effectiveness SE in decibels follows:

$$ SE = 20 \log_{10} \left( \frac{E_{\text{unshielded}}}{E_{\text{shielded}}} \right) = A + R + B $$

where A is absorption loss, R reflection loss, and B multiple reflection correction.

Active Noise Cancellation

Adaptive filters using least mean squares (LMS) algorithms can subtract correlated noise:

$$ y(n) = \sum_{k=0}^{N-1} w_k(n)x(n-k) $$ $$ w_k(n+1) = w_k(n) + \mu e(n)x(n-k) $$

where μ is the convergence factor and e(n) the error signal. This technique is particularly effective against periodic interference like 50/60 Hz power line noise.

Low-Noise Amplifier Design

The noise figure NF of a cascaded system follows Friis' formula:

$$ NF_{\text{total}} = NF_1 + \frac{NF_2 - 1}{G_1} + \frac{NF_3 - 1}{G_1 G_2} + \cdots $$

Key design principles include:

Digital Filtering Methods

Finite impulse response (FIR) filters provide linear phase response:

$$ H(z) = \sum_{n=0}^{N} h[n]z^{-n} $$

While infinite impulse response (IIR) filters offer steeper roll-offs:

$$ H(z) = \frac{\sum_{k=0}^{M} b_k z^{-k}}{1 + \sum_{k=1}^{N} a_k z^{-k}} $$

Wavelet transforms provide multi-resolution analysis for non-stationary noise.

Cryogenic Cooling

For ultra-low noise applications, cooling to liquid helium temperatures (4.2 K) reduces thermal noise:

$$ v_n = \sqrt{4kTR\Delta f} \propto \sqrt{T} $$

Superconducting quantum interference devices (SQUIDs) achieve noise floors below 1 fT/√Hz using this approach.

Noise Reduction System Block Diagram A block diagram illustrating various noise reduction techniques including Faraday cage, twisted pair wiring, adaptive filtering, and cascaded amplifiers with signal flow from left to right. Noise Reduction System Block Diagram Faraday Cage Twisted Pair SE = 20log(f) + 10log(σ) Sₙ(f) LMS Filter w(n+1) = w(n) + μe(n)x(n) Stage 1 Stage 2 Stage 3 NF_total = NF₁ + (NF₂-1)/G₁ + ... H(z) Filter Output Output
Diagram Description: The section covers multiple complex techniques like shielding, adaptive filtering, and cascaded noise figures that would benefit from visual representation of their spatial or signal-flow relationships.

4. Sensitivity, Resolution, and Linearity

4.1 Sensitivity, Resolution, and Linearity

Sensitivity

The sensitivity of a sensor or transducer is defined as the ratio of the change in output signal to the change in the measured input quantity. Mathematically, sensitivity (S) is expressed as:

$$ S = \frac{\Delta V_{\text{out}}}{\Delta Q_{\text{in}}} $$

where ΔVout is the change in output voltage (or other output signal) and ΔQin is the change in the input physical quantity (e.g., temperature, pressure, or displacement). For example, a thermocouple with a sensitivity of 50 µV/°C produces a 50 µV change per degree Celsius of temperature variation.

Resolution

Resolution refers to the smallest detectable change in the input signal that a sensor can reliably distinguish. It is often limited by noise, quantization error (in digital systems), or the physical constraints of the sensing element. For an analog-to-digital converter (ADC), resolution is given by:

$$ \text{Resolution} = \frac{V_{\text{FSR}}}{2^n - 1} $$

where VFSR is the full-scale range of the ADC and n is the number of bits. A 12-bit ADC with a 5V range has a resolution of 1.22 mV. In practical applications, resolution is often degraded by electrical noise, requiring signal conditioning or averaging techniques.

Linearity

Linearity quantifies how closely a sensor's output follows a straight-line relationship with its input. Deviation from ideal linear behavior is expressed as a percentage of full-scale output (FSO). The best-fit straight line is determined via least-squares regression, and nonlinearity error is calculated as:

$$ \text{Nonlinearity (\%)} = \left( \frac{\max |V_{\text{actual}} - V_{\text{ideal}}|}{V_{\text{FSO}}}} \right) \times 100 $$

Common causes of nonlinearity include hysteresis, saturation effects, and material property variations. For instance, strain gauges exhibit slight nonlinearity at high deformations due to the piezoresistive coefficient's dependence on mechanical stress.

Practical Trade-offs

In real-world designs, sensitivity, resolution, and linearity often conflict. A high-sensitivity sensor may introduce nonlinearity due to amplification of small nonlinear effects. Similarly, improving resolution via oversampling reduces bandwidth. Case in point: MEMS accelerometers achieve high resolution (µg/√Hz) at the expense of limited dynamic range, necessitating careful application-specific calibration.

Sensor Output vs. Input Characteristic Input Output Nonlinearity Error
Sensor Linearity Error Visualization A graphical plot showing the nonlinear relationship between sensor input and output, highlighting deviation from ideal linear behavior. Output (V_out) Input (Q_in) 100% 50% 0% 50% 100% Ideal linear response Actual response +5.2% -3.8% +2.1% Ideal linear response Actual response Nonlinearity error
Diagram Description: The diagram would show the nonlinear relationship between sensor input and output, highlighting deviation from ideal linear behavior.

4.2 Accuracy vs. Precision

In sensor and transducer systems, accuracy and precision are distinct but often conflated metrics. Accuracy refers to how close a measurement is to the true value, while precision describes the consistency of repeated measurements under unchanged conditions. A sensor can be precise without being accurate, and vice versa.

Mathematical Definitions

The accuracy of a sensor is quantified by its error relative to a reference standard. For a set of measurements $$x_1, x_2, ..., x_n$$, the mean error $$\mu_e$$ is:

$$ \mu_e = \frac{1}{n} \sum_{i=1}^n (x_i - x_{\text{true}}) $$

where $$x_{\text{true}}$$ is the accepted reference value. Precision, on the other hand, is characterized by the standard deviation $$\sigma$$ of the measurements:

$$ \sigma = \sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2 } $$

where $$\bar{x}$$ is the mean of the measurements.

Visualizing the Difference

Consider a target analogy: high accuracy corresponds to shots clustered near the bullseye, while high precision means tightly grouped shots regardless of their proximity to the target center. Four scenarios emerge:

Practical Implications in Sensor Design

In industrial applications, precision is critical for process control systems where reproducibility matters more than absolute correctness (e.g., semiconductor fabrication). Conversely, scientific instruments like spectrometers prioritize accuracy to ensure validity against fundamental constants. Modern calibration techniques often decouple these metrics—precision is improved via signal averaging or noise reduction, while accuracy is enhanced through traceable calibration standards.

Case Study: Strain Gauge Measurements

A strain gauge with $$\pm 0.1\%$$ precision may still exhibit $$\pm 2\%$$ accuracy due to installation-induced errors (e.g., adhesive thickness). Here, precision reflects the sensor's intrinsic noise floor, while accuracy depends on external factors. Compensation algorithms can mitigate accuracy errors post-measurement, but precision is fundamentally limited by the transducer's signal-to-noise ratio.

Accuracy vs. Precision Target Analogy A target analogy illustrating four scenarios of accuracy and precision combinations using shot groupings relative to a bullseye. True Value High Accuracy Low Precision High Accuracy High Precision Low Accuracy Low Precision Low Accuracy High Precision High Accuracy, Low Precision High Accuracy, High Precision Low Accuracy, Low Precision Low Accuracy, High Precision
Diagram Description: The target analogy for accuracy vs. precision is inherently visual and spatial, showing shot groupings relative to a bullseye.

4.3 Calibration Methods and Standards

Static vs. Dynamic Calibration

Calibration methods are broadly classified into static and dynamic approaches. Static calibration involves applying known constant inputs and recording the sensor's output, typically for linearity, hysteresis, and repeatability analysis. Dynamic calibration, however, subjects the sensor to time-varying inputs (e.g., step, sinusoidal, or impulse signals) to assess frequency response, rise time, and damping characteristics.

$$ y(t) = K \cdot x(t - au) + C $$

where K is the static sensitivity, Ï„ represents time delay, and C accounts for offset errors.

Primary and Secondary Standards

Calibration relies on traceable standards. Primary standards (e.g., NIST-maintained quantum Hall resistance or cesium atomic clocks) define units with ultimate precision. Secondary standards, such as calibrated reference sensors or signal generators, derive their accuracy from primary standards but are practical for lab use. For instance, a Pt100 RTD may serve as a secondary temperature standard after calibration against a primary fixed-point cell.

Least-Squares Regression for Linear Fit

When calibrating a sensor with a presumed linear response, the least-squares method minimizes the sum of squared residuals between measured outputs yi and predicted values Å·i:

$$ \min \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \min \sum_{i=1}^n (y_i - (mx_i + b))^2 $$

The slope m and intercept b are derived analytically:

$$ m = \frac{n\sum x_i y_i - (\sum x_i)(\sum y_i)}{n\sum x_i^2 - (\sum x_i)^2}, \quad b = \frac{\sum y_i - m \sum x_i}{n} $$

Uncertainty Analysis

Calibration uncertainty combines Type A (statistical) and Type B (systematic) components per ISO/IEC Guide 98-3. For a sensor output y with sensitivity coefficients ci, the combined standard uncertainty uc is:

$$ u_c(y) = \sqrt{\sum_{i=1}^N [c_i \cdot u(x_i)]^2} $$

where u(xi) are individual uncertainty contributions from factors like reference instrument error, environmental drift, or quantization.

Automated Calibration Systems

Modern labs employ automated systems with programmable multimeters (e.g., Keysight 3458A), precision sources (e.g., Fluke 5522A), and software like LabVIEW or Python-based scripts. These systems execute:

Traceability and Compliance

ISO 17025 accreditation mandates documented traceability to national standards. A calibration certificate must specify:

Primary Standard Secondary Standard Device Under Test

5. MEMS and Nanotechnology in Sensors

5.1 MEMS and Nanotechnology in Sensors

Fundamentals of MEMS Sensors

Microelectromechanical systems (MEMS) sensors leverage microfabrication techniques to integrate mechanical and electrical components on a single silicon substrate. The governing equation for a typical MEMS accelerometer, based on Newton's second law, is:

$$ F = m \cdot a = k \cdot x $$

where F is the inertial force, m the proof mass, a acceleration, k the spring constant, and x displacement. Capacitive sensing often detects this displacement:

$$ C = \frac{\epsilon_0 \epsilon_r A}{d} $$

where C varies with the gap distance d between parallel plates of area A.

Nanomaterial-Enhanced Sensing

Nanotechnology enables sensors with quantum-scale phenomena. Carbon nanotube (CNT) gas sensors exploit changes in electrical conductivity when target molecules adsorb to their surfaces. The conductance G follows:

$$ G = G_0 + \Delta G \cdot e^{-\frac{E_a}{k_B T}} $$

where G0 is the baseline conductance, ΔG the adsorption-induced change, Ea activation energy, kB Boltzmann's constant, and T temperature.

Fabrication Techniques

Key MEMS processes include:

For nanowire sensors, vapor-liquid-solid (VLS) growth provides precise diameter control down to 5 nm. The growth rate R depends on precursor partial pressure P:

$$ R = C \cdot P \cdot e^{-\frac{E_g}{RT}} $$

Case Study: MEMS/Nano Hybrid Pressure Sensor

A graphene-on-MEMS architecture demonstrates sub-100 mPa resolution. The membrane deflection δ under pressure P follows:

$$ \delta = \frac{3P(1-\nu^2)}{16E} \cdot \frac{a^4}{t^3} $$

where ν is Poisson's ratio, E Young's modulus, a membrane radius, and t thickness. Piezoresistive graphene provides a gauge factor exceeding 200, compared to ~2 for bulk silicon.

Reliability Challenges

Stiction remains a critical failure mode in MEMS devices. The adhesion energy W between surfaces obeys:

$$ W = \frac{3}{4} \pi R \gamma (1 + \cos \theta) $$

where R is asperity radius, γ surface energy, and θ contact angle. Nanocoatings like fluorosilanes reduce γ by 40-60%.

Emerging Applications

MEMS Accelerometer and Graphene Pressure Sensor Structures Side-by-side cross-sections of a MEMS accelerometer (left) with proof mass, springs, and capacitive plates, and a graphene-on-MEMS pressure sensor (right) with labeled components and dimensions. m (proof mass) k (spring) d (gap) d (gap) MEMS Accelerometer δ (deflection) t (thickness) a (radius) Graphene Pressure Sensor
Diagram Description: A diagram would physically show the MEMS accelerometer structure with labeled components (proof mass, springs, capacitive plates) and the graphene-on-MEMS pressure sensor cross-section.

5.2 Wireless Sensor Networks

Architecture and Topology

Wireless sensor networks (WSNs) consist of spatially distributed autonomous sensors that monitor environmental or physical conditions, transmitting data cooperatively to a central location. The topology is typically hierarchical, comprising:

Communication Protocols

WSNs leverage low-power, short-range protocols optimized for energy efficiency and scalability:

Energy Constraints and Optimization

The lifetime of a WSN is dictated by energy consumption, modeled as:

$$ E_{total} = N \cdot \left( E_{sense} + E_{proc} + E_{tx}(d) \right) $$

Where \(E_{tx}(d)\) is the distance-dependent transmission energy, approximated for free-space path loss:

$$ E_{tx}(d) = P_{tx} \cdot \left( \frac{\lambda}{4\pi d} \right)^2 \cdot \frac{1}{\eta} $$

Strategies to minimize energy include:

Localization Techniques

Node positioning is critical for spatially correlated data. Common methods include:

$$ RSSI(d) = P_{tx} - 10n \log_{10}(d) + X_{\sigma} $$

where \(n\) is the path-loss exponent and \(X_{\sigma}\) models shadowing effects.

Security Challenges

WSNs are vulnerable to:

Countermeasures include elliptic-curve cryptography (ECC) for lightweight key exchange and intrusion detection systems (IDS) based on anomaly detection.

Case Study: Environmental Monitoring

A 120-node WSN deployed in rainforests uses LoRaWAN for humidity/temperature tracking. Nodes transmit every 15 minutes, achieving a 5-year lifespan with solar-assisted batteries. Data fusion algorithms suppress outliers caused by foliage-induced multipath fading.

WSN Topology and Protocol Ranges Hierarchical architecture of Wireless Sensor Networks showing sensor nodes, cluster heads, base station, and comparative protocol ranges for IEEE 802.15.4/Zigbee, LoRaWAN, and BLE. Base Station Cluster Head Cluster Head Sensor Nodes LoRaWAN (868 MHz) Zigbee (2.4 GHz) BLE Star Protocol Ranges LoRaWAN Zigbee BLE Star WSN Topology and Protocol Ranges
Diagram Description: The hierarchical architecture of WSNs (sensor nodes → cluster heads → base station) and communication protocols' range/coverage are inherently spatial concepts.

5.3 Smart Sensors and IoT Integration

Architecture of Smart Sensors

Smart sensors integrate sensing, signal processing, and communication capabilities into a single package. The core components include:

Edge Computing in Smart Sensors

Unlike traditional sensors, smart sensors perform in-situ computation to reduce latency and bandwidth usage. Key techniques include:

$$ y[n] = \sum_{k=0}^{N} h[k] \cdot x[n-k] $$

where h[k] represents the filter coefficients for real-time signal processing. Edge AI implementations often use TinyML frameworks like TensorFlow Lite for microcontrollers.

IoT Communication Protocols

Smart sensors leverage standardized protocols for interoperability:

Power Consumption Analysis

The total energy Etotal for a wireless smart sensor node is:

$$ E_{total} = E_{sense} + E_{proc} + E_{tx} $$

where Etx dominates in long-range transmissions. Duty cycling techniques reduce power by periodically activating the radio:

$$ D = \frac{t_{active}}{t_{active} + t_{sleep}} $$

Industrial Applications

Predictive maintenance systems use vibration smart sensors with FFT-based fault detection:

$$ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j2\pi kn/N} $$

Agricultural IoT deploys soil moisture sensors with LoRa backhaul, achieving 10-year battery life through adaptive sampling rates.

Security Challenges

End-to-end encryption (AES-256) and physical unclonable functions (PUFs) address threats in distributed sensor networks. The PUF response R derives from device-specific process variations:

$$ R = f(\Delta V_{th}, \Delta t_{ox}) $$

6. Recommended Books and Journals

6.1 Recommended Books and Journals

6.2 Industry Standards and Datasheets

6.3 Online Resources and Tutorials