Solid State Relay

1. Definition and Basic Operation

Solid State Relay: Definition and Basic Operation

A solid-state relay (SSR) is an electronic switching device that operates without mechanical contacts, unlike traditional electromechanical relays. It employs semiconductor components—such as thyristors, triacs, or power transistors—to perform switching operations, enabling faster response times, higher reliability, and silent operation. SSRs are widely used in industrial automation, power electronics, and precision control systems where mechanical wear and contact arcing are undesirable.

Core Components and Functional Principle

The SSR consists of three primary subsystems:

When a control voltage is applied to the input terminals, the optocoupler's internal LED emits infrared light, activating a photosensitive transistor or thyristor. This triggers the output semiconductor, allowing current to flow through the load. The absence of moving parts eliminates contact bounce and reduces electromagnetic interference (EMI).

Mathematical Modeling of Switching Dynamics

The turn-on time (ton) of an SSR is governed by the optocoupler's response time and the semiconductor's gate charge dynamics. For a MOSFET-based SSR, the turn-on delay can be approximated as:

$$ t_{on} = R_{G} \cdot C_{iss} \cdot \ln\left(\frac{V_{DR}}{V_{DR} - V_{TH}}\right) $$

where RG is the gate resistance, Ciss is the input capacitance, VDR is the driver voltage, and VTH is the threshold voltage. In AC SSRs with zero-crossing detection, the maximum turn-on delay is half the AC cycle (8.3 ms for 60 Hz systems).

Advantages Over Electromechanical Relays

Practical Considerations

SSRs require careful thermal management due to I2R losses in the output semiconductor. The power dissipation (PD) is calculated as:

$$ P_{D} = I_{RMS}^2 \cdot R_{DS(on)} + V_{f} \cdot I_{AVG} $$

where RDS(on) is the on-state resistance (for MOSFETs) and Vf is the forward voltage drop (for TRIACs). Heat sinks or forced-air cooling are often necessary for currents exceeding 5 A.

This section provides a rigorous technical foundation for understanding SSRs, balancing theory with practical design considerations. The mathematical derivations and component-level explanations cater to advanced readers while maintaining readability through logical flow and hierarchical structuring.
SSR Internal Block Diagram Block diagram of a Solid State Relay showing internal subsystems: input circuit, trigger/driver circuit, and output switching element with signal flow. Input Circuit Optocoupler Trigger Circuit (Zero-crossing) TRIAC (Output) Load V_DR V_TH I_RMS
Diagram Description: The diagram would show the internal subsystems (input circuit, trigger/driver circuit, output switching element) and their signal flow, which is spatial and not fully conveyed by text alone.

1.2 Comparison with Electromechanical Relays

Solid-state relays (SSRs) and electromechanical relays (EMRs) serve the same fundamental purpose of switching electrical loads, but their operational principles, performance characteristics, and application suitability differ significantly. The key distinctions arise from the absence of moving parts in SSRs, which rely on semiconductor switching elements such as thyristors, TRIACs, or MOSFETs, whereas EMRs employ physical contacts actuated by an electromagnetic coil.

Switching Speed and Lifetime

SSRs exhibit switching times in the range of microseconds to milliseconds, orders of magnitude faster than EMRs, which typically require 5–15 ms due to mechanical inertia. The absence of contact bounce in SSRs eliminates arcing, enabling reliable high-frequency switching. The lifetime of an SSR is primarily determined by semiconductor aging, often exceeding 108 cycles, whereas EMRs degrade due to contact wear, typically lasting 105–106 cycles under rated load.

Power Dissipation and Efficiency

EMRs exhibit low contact resistance (∼50 mΩ) when closed, resulting in minimal conduction losses. However, SSRs introduce forward voltage drops (1–2 V for MOSFET-based, higher for thyristors), leading to Joule heating proportional to load current:

$$ P_{diss} = I_{load} \cdot V_{drop} $$

For high-current applications, this necessitates careful thermal management. Conversely, EMRs dissipate power primarily in the actuation coil, independent of load current.

Noise and EMI Characteristics

The abrupt current interruption in EMRs generates voltage transients (L di/dt effects) and broadband electromagnetic interference. SSRs mitigate this through zero-crossing switching (for AC) or controlled slew rates in DC applications. However, high-frequency SSRs using fast semiconductors may produce higher-frequency harmonics requiring additional filtering.

Environmental Sensitivity

SSRs demonstrate superior performance in high-vibration environments and contaminated atmospheres where particulate matter could impede EMR contact movement. However, semiconductor junctions in SSRs are more susceptible to damage from voltage transients (dV/dt) and require robust snubber circuits or varistor protection. EMRs naturally withstand higher surge currents due to their physical contact geometry.

Load Compatibility

EMRs can switch both AC and DC loads indiscriminately, whereas SSRs are typically optimized for one or the other due to semiconductor physics. Specialized SSRs exist for:

Notably, SSRs excel in capacitive or inductive load switching where EMRs would suffer from contact welding during inrush currents.

Failure Modes

EMRs tend to fail open-circuit due to contact oxidation or welding, while SSRs more commonly fail short-circuit from semiconductor breakdown. This distinction critically impacts fail-safe design considerations in safety-critical systems.

1.3 Key Components and Internal Structure

Optocoupler (Input Stage)

The input stage of an SSR typically consists of an optocoupler, which electrically isolates the control circuit from the load. The optocoupler contains an infrared LED paired with a photosensitive device (e.g., photodiode, phototransistor, or phototriac). When a control voltage is applied, the LED emits light, triggering the photosensor. This galvanic isolation prevents ground loops and high-voltage transients from propagating to the low-voltage control side.

Trigger Circuit

The trigger circuit conditions the signal from the optocoupler to drive the output switching device. In AC SSRs, this often includes a zero-crossing detector to synchronize switching with the AC waveform, minimizing inrush currents. The trigger may use a Schmitt trigger or comparator to ensure clean transitions, with hysteresis to prevent chatter near threshold voltages.

Output Switching Device

The core of the SSR is its semiconductor-based output switch, which replaces the mechanical contacts of electromechanical relays. Common configurations include:

Snubber Circuit

AC SSRs often incorporate an RC snubber network across the output to suppress voltage spikes caused by inductive load switching. The snubber dissipates energy during dV/dt transients, preventing false triggering or device breakdown. The time constant is designed to satisfy:

$$ \tau = R_{snub}C_{snub} > \frac{1}{2\pi f_{noise}} $$

Heat Sink Interface

Power dissipation in the output switch follows:

$$ P_{diss} = I_{load}^2 R_{DS(on)} + E_{sw}f_{sw} $$

where RDS(on) is the on-state resistance and Esw is the switching energy. A thermally conductive pad or compound ensures efficient heat transfer to an external heat sink, with thermal resistance θJA dictating maximum current ratings.

Protection Circuits

Advanced SSRs integrate:

Solid State Relay Internal Structure Block diagram showing the internal structure of a Solid State Relay (SSR), including optocoupler, trigger circuit, output switching device, and protection circuits with signal flow. LED Photo-diode Optocoupler Zero-crossing Trigger Circuit Triac Output Stage RC Snubber TVS Diode Protection Heat Sink Thermal Pad Solid State Relay Internal Structure
Diagram Description: The diagram would physically show the internal structure of an SSR, including the optocoupler, trigger circuit, output switching device, and protection circuits, with their interconnections.

2. AC Output SSRs

2.1 AC Output SSRs

Operating Principle

AC output solid-state relays (SSRs) use thyristors (SCRs or TRIACs) as the switching element, enabling zero-crossing or random-phase switching of AC loads. The gate drive circuit is optically isolated, typically employing an infrared LED coupled to a photosensitive thyristor or MOSFET driver. When the input control signal activates the LED, the photodetector triggers the thyristor's gate, allowing current flow during the appropriate half-cycle of the AC waveform.

$$ I_{load}(t) = \frac{V_{AC}(t)}{R_{load}} \quad \text{where} \quad V_{AC}(t) = V_{pk} \sin(\omega t) $$

Zero-Crossing vs. Random-Phase Switching

Zero-crossing SSRs activate the thyristor only when the AC voltage crosses zero, minimizing inrush current and electromagnetic interference (EMI). This is achieved through additional zero-cross detection circuitry:

Random-phase SSRs can trigger at any point in the AC cycle, enabling phase-angle control for applications like dimming or power regulation:

$$ P_{avg} = \frac{V_{rms}^2}{R_{load}} \left( \frac{1}{\pi} (\pi - \alpha + \frac{\sin 2\alpha}{2}) \right) $$

where α is the firing angle delay from zero-cross.

Thermal Considerations

Thyristor-based SSRs exhibit forward voltage drops (1-2 V) that generate significant heat at high currents:

$$ P_{diss} = I_{load} \cdot V_{on} + I_{leakage} \cdot V_{AC} $$

Proper heatsinking is critical, with thermal resistance calculations following:

$$ T_j = T_a + (R_{θjc} + R_{θcs} + R_{θsa}) \cdot P_{diss} $$

Snubber Circuits

AC SSRs require RC snubber networks (typically 100 Ω + 0.1 μF) across the thyristor to:

TRIAC R C

Practical Design Constraints

Key parameters for AC SSR selection include:

AC SSR Switching Waveforms AC voltage waveform showing zero-crossing and phase-angle triggering points with labeled conduction periods and firing angles. Time V Zero-cross Zero-cross Zero-cross α Trigger V_AC(t) Conduction Period
Diagram Description: The section describes zero-crossing vs. random-phase switching and thyristor operation, which are best visualized with AC waveforms and triggering points.

2.2 DC Output SSRs

DC output solid-state relays (SSRs) are designed to switch DC loads, leveraging semiconductor components such as power MOSFETs or insulated-gate bipolar transistors (IGBTs) instead of mechanical contacts. Unlike AC SSRs, which rely on zero-crossing detection for switching, DC SSRs must handle continuous current flow, requiring careful consideration of voltage drop, heat dissipation, and transient suppression.

Operating Principle

DC SSRs typically employ an optocoupler or transformer-based isolation to separate the low-voltage control circuit from the high-power DC load. The input side activates an LED or primary winding, inducing a signal in the output stage that drives the gate of a power MOSFET or IGBT. The absence of moving parts eliminates arcing, making DC SSRs ideal for high-cycle applications.

$$ R_{DS(on)} = \frac{V_{drop}}{I_{load}} $$

where RDS(on) is the on-state resistance of the MOSFET, Vdrop is the voltage drop across the SSR, and Iload is the load current. Minimizing RDS(on) is critical to reducing power dissipation.

Key Design Considerations

Applications

DC SSRs are widely used in:

Transient Suppression

Inductive loads necessitate protection against voltage spikes. A freewheeling diode or transient voltage suppressor (TVS) is often placed across the load. The energy dissipated during turn-off is given by:

$$ E = \frac{1}{2} LI^2 $$

where L is the load inductance and I is the interrupted current.

2.3 AC/DC Input SSRs

Solid-state relays with AC or DC input control are distinguished by their input signal compatibility. The input circuit of an SSR determines its triggering mechanism, isolation method, and compatibility with different control systems. AC-input SSRs typically use a triac or back-to-back thyristors for switching, while DC-input SSRs rely on MOSFETs or IGBTs.

Input Circuit Topologies

The input stage of an SSR consists of an optocoupler or transformer-based isolation barrier, followed by a triggering circuit. For DC-input SSRs, the optocoupler's LED is driven directly by a DC voltage (typically 3–32 V). AC-input SSRs incorporate a bridge rectifier to convert the AC signal to DC before driving the optocoupler.

$$ V_{in(min)} = I_{LED} \cdot R_{lim} + V_{LED} $$

where VLED is the forward voltage drop of the optocoupler's LED (typically 1.2–1.5 V), ILED is the minimum required LED current (2–20 mA), and Rlim is the current-limiting resistor.

AC Input Considerations

AC-input SSRs must account for zero-crossing behavior in the control signal. The rectified input produces a pulsating DC waveform, requiring careful design of the current-limiting network to ensure reliable optocoupler operation throughout the AC cycle. The input impedance Zin is given by:

$$ Z_{in} = \frac{V_{RMS}}{I_{RMS}} $$

where VRMS is the RMS input voltage and IRMS is the RMS input current. Typical input impedance values range from 1 kΩ to 10 kΩ.

DC Input Characteristics

DC-input SSRs exhibit a well-defined threshold voltage, making them suitable for low-voltage control systems. The input current Iin is determined by:

$$ I_{in} = \frac{V_{in} - V_{LED}}{R_{lim}} $$

where Vin is the applied DC voltage. Care must be taken to avoid exceeding the optocoupler's maximum rated current (typically 50–100 mA).

Switching Dynamics and Isolation

The isolation voltage between input and output circuits ranges from 2.5 kV to 6 kV for standard SSRs. High-voltage applications may require reinforced isolation (>10 kV). The input-to-output capacitance Cio (typically 1–10 pF) affects high-frequency noise coupling and must be minimized in sensitive applications.

Practical Design Considerations

Modern hybrid SSRs combine the advantages of both types, featuring universal input circuits that accept either AC or DC control signals while maintaining galvanic isolation.

AC/DC Input SSR Circuit Comparison Side-by-side comparison of AC and DC input solid-state relay circuits, highlighting the bridge rectifier, optocoupler, and switching components. AC/DC Input SSR Circuit Comparison AC Input Bridge Rectifier Z_in R_lim V_LED, I_LED Isolation Thyristor Output DC Input Z_in R_lim V_LED, I_LED Isolation MOSFET Output AC Input SSR DC Input SSR
Diagram Description: The section describes AC/DC input circuit topologies with rectifiers, optocouplers, and switching components, which are inherently spatial relationships.

Zero-Crossing and Instant-On SSRs

Solid-state relays (SSRs) are broadly classified based on their switching behavior relative to the AC waveform. The two primary modes are zero-crossing and instant-on (also called random turn-on), each optimized for distinct applications. The choice between these depends on the load characteristics, electromagnetic interference (EMI) constraints, and switching speed requirements.

Zero-Crossing SSRs

Zero-crossing SSRs activate the load only when the AC voltage waveform crosses zero volts. This is achieved using an internal zero-crossing detection circuit, typically implemented with a comparator or optocoupler synchronized to the AC cycle. The mathematical condition for triggering is:

$$ V(t) = V_{\text{peak}} \sin(2\pi ft) = 0 $$

where V(t) is the instantaneous voltage, Vpeak is the peak voltage, and f is the line frequency. The relay introduces a small delay (td) to ensure switching occurs within a narrow window around the zero-crossing point, typically ±10 ms for 50/60 Hz systems.

Advantages of zero-crossing SSRs include:

However, zero-crossing SSRs are unsuitable for phase-controlled applications like dimming or motor speed control due to their inherent latency.

Instant-On SSRs

Instant-on SSRs activate the load immediately upon receiving a control signal, regardless of the AC phase. This is critical for applications requiring precise timing, such as:

The turn-on time (ton) for instant-on SSRs is typically under 1 ms, governed by the equation:

$$ t_{\text{on}} = R_g C_{\text{iss}} \ln \left( \frac{V_{\text{drive}}}{V_{\text{th}}} \right) $$

where Rg is the gate resistance, Ciss is the input capacitance of the switching device (e.g., MOSFET or TRIAC), Vdrive is the control voltage, and Vth is the threshold voltage.

Drawbacks include:

Practical Considerations

For inductive loads (e.g., motors, transformers), zero-crossing SSRs can cause voltage spikes due to abrupt current interruption. A snubber circuit (e.g., an RC network) is often added to mitigate this. The snubber values can be derived from:

$$ R_{\text{snub}} = \frac{V_{\text{peak}}}{I_{\text{leakage}}} \quad \text{and} \quad C_{\text{snub}} = \frac{I_{\text{leakage}} t_{\text{fall}}}{V_{\text{peak}}} $$

where Ileakage is the leakage current and tfall is the fall time of the SSR.

Zero-Crossing vs. Instant-On SSR Switching Waveforms A side-by-side comparison of zero-crossing and instant-on switching waveforms in solid-state relays, showing AC voltage, triggering events, and timing delays. Zero-Crossing vs. Instant-On SSR Switching Waveforms 0V Time Zero-Crossing SSR Zero-Crossing Zero-Crossing Vpeak Instant-On SSR td ton Vpeak
Diagram Description: The section discusses voltage waveforms (zero-crossing vs. instant-on switching) and their timing relationships, which are inherently visual concepts.

3. Switching Mechanism

3.1 Switching Mechanism

The switching mechanism of a solid-state relay (SSR) relies on semiconductor devices rather than electromechanical contacts. Unlike traditional relays, SSRs use optocouplers, thyristors, or MOSFETs to achieve isolation and control between input and output circuits. The absence of moving parts eliminates mechanical wear, enabling faster switching speeds and higher reliability.

Optocoupler-Based Isolation

The input side of an SSR typically consists of an infrared LED, which emits light when activated by a control signal. This light is detected by a photodetector (e.g., a photodiode or phototransistor) on the output side, creating an electrically isolated trigger for the switching element. The optocoupler ensures galvanic isolation, often rated for several kilovolts.

Thyristor and Triac Switching

For AC load control, SSRs commonly employ thyristors (SCRs) or triacs. When the optocoupler triggers the gate, the thyristor enters conduction at the next zero-crossing of the AC waveform, minimizing inrush current. The turn-off occurs when the current drops below the holding threshold, typically at the next zero-crossing.

$$ I_{hold} = \frac{V_{peak}}{R_{load}} \sin(2\pi f t) $$

where Ihold is the holding current, Vpeak is the peak voltage, and Rload is the load resistance.

MOSFET-Based DC Switching

In DC applications, power MOSFETs are preferred due to their low on-resistance (RDS(on)) and fast switching. A back-to-back MOSFET configuration blocks current in both directions, essential for bidirectional isolation. The gate is driven by the optocoupler's output, often via an additional amplifier stage for high-current loads.

$$ P_{loss} = I_{load}^2 \cdot R_{DS(on)} $$

where Ploss is the conduction loss and Iload is the load current.

Zero-Crossing vs. Random Turn-On

Zero-crossing SSRs synchronize switching with the AC waveform's zero-voltage point, reducing electromagnetic interference (EMI) and inrush currents. Random-turn SSRs activate immediately upon input signal application, suitable for phase-angle control in dimming or motor speed regulation.

Thermal Considerations

Junction heating in the semiconductor switch must be managed to prevent failure. The thermal resistance (θJA) and maximum junction temperature (TJ(max)) dictate the permissible power dissipation:

$$ T_J = T_A + P_{loss} \cdot \theta_{JA} $$

where TJ is the junction temperature and TA is the ambient temperature.

SSR Internal Architecture and Waveforms Schematic of a solid state relay showing optocoupler isolation, thyristor switching with zero-crossing detection, MOSFET configuration, and synchronized AC waveform. Input Optocoupler Thyristor I_hold R_DS(on) MOSFET Pair Load θ_JA Zero-Crossing Zero-Crossing V_peak AC Waveform SSR Internal Architecture and Waveforms
Diagram Description: The section describes optocoupler isolation, thyristor switching with zero-crossing, and MOSFET configurations—all highly visual concepts requiring spatial representation of components and signal flow.

3.2 Load Compatibility and Voltage Ratings

Load Types and Switching Characteristics

Solid-state relays (SSRs) exhibit distinct performance characteristics depending on the nature of the load. Resistive loads, such as heating elements, present minimal challenges due to their linear current-voltage relationship. However, inductive loads (motors, solenoids) and capacitive loads (power supplies, LED drivers) introduce transient behaviors that must be accounted for in SSR selection.

The inrush current for inductive loads can be derived from the time-domain solution of the RL circuit:

$$ i(t) = \frac{V}{R} \left(1 - e^{-t/\tau}\right) $$

where τ = L/R is the time constant. For a motor with L = 50 mH and R = 10 Ω, the peak inrush current can reach 2-3 times the steady-state value during the first few milliseconds.

Voltage Ratings and Derating Factors

The maximum voltage rating of an SSR is determined by the blocking capability of its output semiconductor devices (typically MOSFETs or thyristors). However, three critical factors necessitate derating:

A practical design guideline is to select an SSR with a voltage rating of at least 2× the RMS line voltage. For 240V AC systems, this implies:

$$ V_{SSR} \geq 2 \times 240V \times 1.1 = 528V $$

Current Handling and Thermal Considerations

The current rating of an SSR is primarily constrained by the power dissipation in the output devices. The total power loss comprises:

$$ P_{total} = I_{RMS}^2 R_{DS(on)} + Q_{rr} V_{block} f_{sw} $$

where Qrr is the reverse recovery charge and fsw the switching frequency. For a 40A SSR with RDS(on) = 25mΩ operating at 30A RMS:

$$ P_{cond} = (30A)^2 \times 0.025Ω = 22.5W $$

This dissipation requires careful thermal management, as the junction-to-case thermal resistance (θJC) of typical power MOSFET packages ranges from 0.5-2°C/W.

AC vs DC Load Switching

AC-output SSRs leverage zero-crossing detection to minimize switching losses and EMI. The turn-on occurs when:

$$ V_{AC}(t) = V_{peak} \sin(2πft) ≈ 0 $$

DC-output SSRs must handle continuous current without the benefit of natural zero crossings. This necessitates:

Surge Protection Requirements

Transient voltage suppressors (TVS diodes) must be sized according to the clamping voltage VC and peak pulse power PPP:

$$ P_{PP} = \frac{V_C^2}{R_{load}} \times t_{surge} $$

For a 100V surge lasting 50μs into a 50Ω load with VC = 150V:

$$ P_{PP} = \frac{(150V)^2}{50Ω} \times 50μs = 22.5mJ $$

This energy handling capability must be derated by 20-40% for high-reliability applications.

SSR Load Switching Characteristics A diagram illustrating SSR load switching characteristics, including inductive load current waveform, AC zero-crossing points, DC switching SOA curve, and TVS diode clamping action. R L i(t) = Iâ‚€(1 - e^(-t/Ï„)) Ï„ = L/R Zero-Crossing Zero-Crossing V_peak Current Voltage Q_rr R_DS(on) V_C
Diagram Description: The section discusses time-domain behaviors of inductive loads and AC/DC switching characteristics, which are best visualized with waveforms and circuit diagrams.

3.3 Thermal Management and Heat Dissipation

Thermal management in solid-state relays (SSRs) is critical due to power dissipation primarily occurring in the semiconductor junction. The total power loss Ploss in an SSR consists of conduction losses, switching losses (in AC SSRs), and leakage losses, given by:

$$ P_{loss} = I_{rms}^2 R_{on} + E_{sw} f_{sw} + I_{leak} V_{block} $$

where Irms is the load current, Ron the on-state resistance, Esw the switching energy, fsw the switching frequency, and Ileak the leakage current under blocking voltage Vblock.

Thermal Resistance Modeling

The junction temperature Tj must be kept below the maximum rated value (typically 125°C–150°C for silicon devices). The thermal path is modeled as a series of thermal resistances:

$$ T_j = T_a + P_{loss} ( heta_{jc} + heta_{cs} + heta_{sa}) $$

where:

Heatsink Design Considerations

Forced air cooling or oversized heatsinks are required for high-current SSRs. The required heatsink thermal resistance is derived by rearranging the thermal equation:

$$ heta_{sa} \leq \frac{T_{j,max} - T_a}{P_{loss}} - ( heta_{jc} + heta_{cs}) $$

For example, a 40A SSR with Ron = 5mΩ dissipating 8W at 50°C ambient with θjc = 1.2°C/W and θcs = 0.5°C/W (using thermal grease) requires:

$$ heta_{sa} \leq \frac{125 - 50}{8} - (1.2 + 0.5) = 7.8°C/W $$

Transient Thermal Analysis

Under pulsed loads, the thermal impedance Zth(j-a)(t) must be considered instead of steady-state θja. The Foster network model approximates this as:

$$ Z_{th}(t) = \sum_{i=1}^n R_i \left(1 - e^{-t/ au_i}\right) $$

where Ri and Ï„i (=RiCi) are extracted from the device datasheet.

Practical Implementation

Junction θjc Case θcs Heatsink θsa Ambient
Thermal Resistance Network in SSR A block diagram illustrating the thermal resistance network from junction to ambient in a Solid State Relay (SSR), showing heat flow through components with labeled thermal resistances. Junction Case Heatsink Ambient θjc θcs θsa Heat Flow Thermal Resistance Network in SSR
Diagram Description: The diagram would physically show the thermal resistance network from junction to ambient, illustrating the sequential path of heat flow through different components.

4. Industrial Automation

4.1 Industrial Automation

Role of Solid State Relays in Industrial Control Systems

Solid state relays (SSRs) are favored in industrial automation for their ability to switch high-voltage AC/DC loads with zero mechanical wear. Unlike electromechanical relays, SSRs employ semiconductor switching elements (typically thyristors, TRIACs, or MOSFETs) optically isolated from the control circuit. This eliminates contact bounce and arcing, critical in environments with explosive gases or frequent cycling.

Key Performance Metrics

The switching efficiency of an SSR in industrial applications is governed by:

$$ P_{loss} = I_{load}^2 R_{on} + V_{off} I_{leakage} $$

where Ron is the on-state resistance (typically 10–100 mΩ for high-current SSRs) and Voff is the blocking voltage. Industrial SSRs achieve thermal stability through:

Noise Immunity and Transient Protection

Industrial SSRs integrate snubber circuits to suppress dV/dt-induced false triggering. A typical RC snubber for a 480VAC system uses:

$$ R_{snub} = \frac{V_{peak}}{0.1 I_{load}},\quad C_{snub} = \frac{I_{load}}{2\pi f V_{peak}} $$

For harsh environments, SSRs incorporate:

Real-World Implementation: Motor Control

In three-phase motor starters, SSRs enable soft-start functionality by phase-angle control. The gate drive timing for a TRIAC-based SSR is derived from:

$$ \alpha = \cos^{-1}\left(\frac{2V_{target}}{V_{supply}} - 1\right) $$

where α is the firing angle delay. Modern industrial SSRs achieve switching times < 100μs, enabling PWM frequencies up to 1kHz for precision torque control.

Case Study: Packaging Line Automation

A high-speed bottling plant replaced electromechanical relays with optically isolated SSRs (Crydom D2425 series), resulting in:

Thermal Management Strategies

Industrial SSRs dissipate heat through:

The maximum junction temperature is constrained by:

$$ T_j = T_a + P_{loss} (θ_{JC} + θ_{CS} + θ_{SA}) $$

where θCS is the thermal interface material resistance and θSA is the sink-to-ambient resistance.

TRIAC Phase-Angle Control & Thermal Resistance Model A diagram showing TRIAC phase-angle control (top) with AC voltage waveform and firing angle delay (α), and thermal resistance model (bottom) with θJC, θCS, θSA components. α Time Voltage TRIAC Phase-Angle Control Gate Signal V_supply θJC θCS θSA T_j T_a Thermal Resistance Model
Diagram Description: The section involves complex voltage waveforms (TRIAC firing angle control) and thermal resistance relationships that are spatial in nature.

4.2 HVAC Systems

Solid State Relay Fundamentals in HVAC Applications

Solid state relays (SSRs) provide superior performance compared to electromechanical relays in HVAC systems due to their lack of moving parts, silent operation, and faster switching speeds. The core mechanism involves optically isolated semiconductor switching elements (typically TRIACs for AC loads or MOSFETs/IGBTs for DC) that are triggered by low-voltage control signals. The absence of contact arcing enables SSRs to achieve >106 switching cycles in typical HVAC duty cycles, compared to 105 cycles for electromechanical relays.

$$ R_{th(j-a)} = R_{th(j-c)} + R_{th(c-h)} + R_{th(h-a)} $$

Where thermal resistance from junction to ambient (Rth(j-a)) determines maximum current handling capacity in HVAC environments. Proper heat sinking is critical as compressor startups can produce transient currents 6-8× rated load.

Load Characteristics and Switching Considerations

HVAC systems present unique SSR challenges due to:

Compressor Load Profile

Advanced Protection Circuitry

Modern HVAC SSRs incorporate multiple protection layers:

$$ V_{TVS} = 1.3 \times \sqrt{2} \times V_{RMS} + 20\% $$

Transient voltage suppressors (TVS diodes) are sized using this relation, while gate drive circuits often implement:

Energy Efficiency Optimization

SSRs contribute to HVAC energy efficiency through:

$$ \eta_{SSR} = \frac{P_{out}}{P_{out} + I_{leakage}^2R_{on} + P_{gate}} \approx 99.8\% $$
HVAC SSR Load Characteristics and Protection Diagram showing compressor load profile with inrush current and inductive kickback, along with protection circuits including snubber RC network, TVS diode, and zero-crossing detector. Time Current Inrush Current (6-8× rated) Inductive Kickback R C Snubber RC Network (t>10μs) TVS Diode (V_{TVS} = V_{BR} + V_{CL}) Zero-Crossing Detector Zero-Crossing Point HVAC SSR Load Characteristics and Protection
Diagram Description: The section discusses complex interactions like inductive kickback, inrush currents, and zero-crossing requirements that involve time-domain behavior and electrical waveforms.

4.3 Medical Equipment

Solid-state relays (SSRs) are indispensable in modern medical devices due to their silent operation, absence of mechanical wear, and immunity to electromagnetic interference (EMI). Unlike electromechanical relays, SSRs eliminate contact bounce and arcing, critical in sensitive environments like operating rooms and diagnostic labs. Their fast switching speeds (typically <1 ms) enable precise control in applications such as defibrillators, infusion pumps, and MRI systems.

Noise-Sensitive Applications

Medical imaging systems, particularly MRI machines, demand ultra-low noise switching to prevent artifacts in acquired images. SSRs with optically isolated MOSFET or thyristor-based outputs achieve this by:

$$ I_{leakage} = \frac{V_{supply}}{R_{isolation}} \leq 10^{-6} \text{A} $$

Patient Safety Considerations

SSRs in life-support equipment must adhere to IEC 60601-1's means of patient protection (MOPP) requirements. Key design parameters include:

Opto-Isolator MOSFET Array Patient Isolation Barrier

Thermal Management in Implantable Devices

For implantable neurostimulators or pacemakers, SSRs must minimize joule heating. Power dissipation is given by:

$$ P_{diss} = I_{load}^2 \cdot R_{DS(on)} + Q_g \cdot V_{drive} \cdot f_{sw} $$

Where RDS(on) is typically <50 mΩ for medical-grade SSRs, and Qg is kept below 10 nC through advanced packaging like wafer-level chip-scale (WLCSP) designs.

Case Study: Electrosurgical Units

In RF ablation systems operating at 300-500 kHz, SSRs replace mechanical relays for:

4.4 Consumer Electronics

Solid-state relays (SSRs) are increasingly favored in consumer electronics due to their silent operation, longevity, and absence of mechanical wear. Unlike electromechanical relays, SSRs leverage semiconductor switching elements (e.g., MOSFETs, TRIACs, or thyristors) to isolate and control loads, making them ideal for noise-sensitive applications like audio equipment, smart home devices, and precision instrumentation.

Key Advantages in Consumer Applications

Circuit Design Considerations

SSRs introduce unique challenges in consumer electronics, such as leakage currents and thermal management. For a TRIAC-based SSR driving a 120V AC load, the leakage current Ileak can be derived from the TRIAC's off-state impedance Zoff:

$$ I_{leak} = \frac{V_{RMS}}{Z_{off}} $$

For a typical Zoff of 10 MΩ, Ileak ≈ 12 µA—sufficient to trigger false activations in high-impedance circuits. Mitigation strategies include:

Thermal Analysis

Power dissipation Pdiss in an SSR stems from conduction losses and switching losses. For a MOSFET-based SSR with RDS(on) = 50 mΩ and Iload = 2A:

$$ P_{diss} = I_{load}^2 \times R_{DS(on)} = (2)^2 \times 0.05 = 0.2 \text{ W} $$

This necessitates thermal derating in compact enclosures. The junction-to-ambient thermal resistance θJA dictates the maximum allowable dissipation:

$$ T_j = T_a + (P_{diss} \times \theta_{JA}) $$

Real-World Implementations

Modern smart thermostats employ SSRs for silent zone control, leveraging zero-crossing detection to minimize EMI. High-end coffee makers use SSRs for precise temperature regulation, exploiting their fast switching (<1 ms) for PID-controlled heating elements.

Optocoupler TRIAC

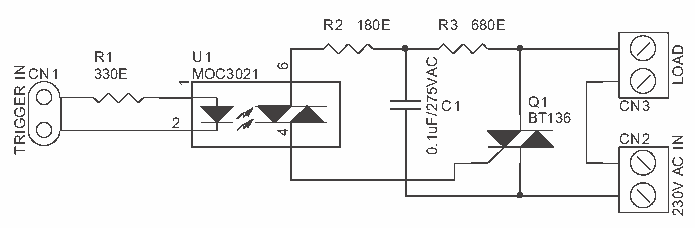
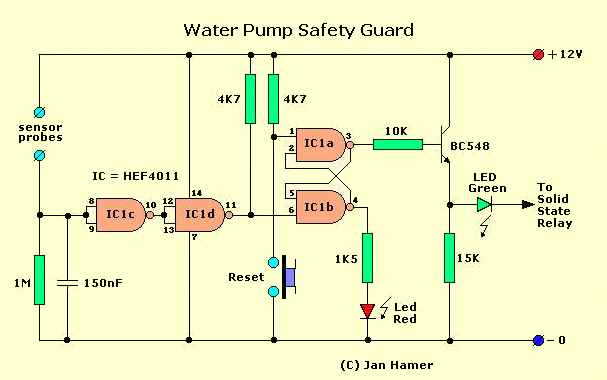
The diagram above illustrates a typical AC load control circuit, where an optocoupler isolates the low-voltage control signal from the high-voltage TRIAC stage.

SSR Optocoupler-TRIAC Isolation Circuit A schematic diagram illustrating the optocoupler-TRIAC isolation circuit in a solid-state relay, showing signal flow from the control input to the load. Optocoupler LED (Input) Photodetector Isolation Barrier TRIAC Main Terminal 1 Main Terminal 2 Gate Control Signal Load
Diagram Description: The diagram would physically show the optocoupler-TRIAC isolation circuit and signal flow path, which is central to understanding SSR operation in consumer electronics.

5. Benefits Over Electromechanical Relays

5.1 Benefits Over Electromechanical Relays

No Moving Parts and Mechanical Wear

Solid-state relays (SSRs) eliminate mechanical contacts, relying instead on semiconductor switching elements such as thyristors, triacs, or MOSFETs. Unlike electromechanical relays (EMRs), which suffer from contact erosion due to arcing during switching, SSRs experience no wear from repeated operation. The absence of moving parts ensures a longer operational lifespan, often exceeding 108 cycles compared to 105–106 cycles for EMRs.

Faster Switching Speeds

SSRs achieve switching times in the microsecond range, whereas EMRs typically require milliseconds due to mechanical inertia. The delay in EMRs arises from the coil magnetization and physical movement of the armature. For high-frequency applications, such as pulse-width modulation (PWM) or rapid load control, SSRs provide superior performance without bounce or contact chatter.

$$ t_{switch} = \frac{L}{R} \ln\left(\frac{V_{coil}}{V_{coil} - I_{pickup} R}\right) $$

where L and R are the coil inductance and resistance, Vcoil is the drive voltage, and Ipickup is the minimum actuation current. SSRs bypass this delay entirely.

Silent Operation and Reduced EMI

Electromechanical relays generate audible noise during contact closure and release, along with electromagnetic interference (EMI) from arcing. SSRs operate silently and produce minimal EMI since switching occurs at zero-crossing (for AC SSRs) or without abrupt current interruptions. This makes them ideal for noise-sensitive environments like medical equipment or laboratory instrumentation.

Higher Reliability in Harsh Environments

SSRs are immune to vibration, shock, and contamination—common failure modes for EMRs. Hermetically sealed optocouplers in SSRs prevent oxidation and degradation in humid or dusty conditions. Industrial applications, such as factory automation or automotive systems, benefit from this robustness.

Lower Power Consumption

EMRs require continuous coil current to maintain contact closure, dissipating power as I2R losses. SSRs only draw minimal gate-drive current, reducing steady-state power dissipation. For battery-powered or energy-efficient designs, this translates to significant savings.

$$ P_{diss} = I_{coil}^2 R_{coil} \quad \text{(EMR)} $$ $$ P_{diss} = V_{f} I_{LED} \quad \text{(SSR)} $$

where Vf is the forward voltage of the SSR's input LED.

Compact Form Factor

With no need for bulky coils or contact assemblies, SSRs occupy less board space. High-density PCBs and modular systems leverage this advantage, particularly in consumer electronics and telecom infrastructure.

5.2 Common Challenges and Mitigation Strategies

Thermal Management and Heat Dissipation

Solid state relays (SSRs) generate heat due to on-state voltage drop (VON) and switching losses. The power dissipation (PD) in an SSR is given by:

$$ P_D = I_{LOAD}^2 \cdot R_{DS(ON)} + (E_{SW} \cdot f_{SW}) $$

where ILOAD is the load current, RDS(ON) is the on-resistance of the MOSFET/thyristor, ESW is the switching energy, and fSW is the switching frequency. Excessive heat reduces reliability and can trigger thermal shutdown. Mitigation strategies include:

Voltage Transients and Surge Protection

SSRs are susceptible to voltage spikes from inductive loads (e.g., motors, solenoids). The dv/dt rating of the SSR must exceed the transient slew rate to prevent false triggering. A common mitigation approach involves:

Leakage Current and Off-State Isolation

In the off state, SSRs exhibit leakage currents (typically 1–10mA) due to parasitic capacitance in the output semiconductor. This can cause:

Solutions include:

Zero-Crossing Artifacts in AC Switching

Zero-crossing SSRs introduce timing jitter (Δt) due to internal comparator delays, causing phase asymmetry in AC waveforms. The resulting DC offset (VDC) is:

$$ V_{DC} = \frac{1}{T} \int_0^T V(t) \, dt \approx \frac{V_{PEAK} \cdot \Delta t}{\pi \cdot T} $$

where T is the AC period. This can saturate transformer-coupled loads. Mitigation involves:

EMI and Radio Frequency Interference (RFI)

Fast switching (especially in DC SSRs) generates broadband EMI. Radiated emissions follow:

$$ E \propto \frac{dI}{dt} \cdot \frac{A \cdot f^2}{r} $$

where A is the loop area, f is the harmonic frequency, and r is the distance. Countermeasures include:

Zero-Crossing SSR Timing Jitter and DC Offset A waveform diagram showing ideal vs. actual zero-crossing switching (top) and the resulting DC offset (bottom). Δt V_PEAK Zero-Crossing SSR Timing Jitter Time (T) Voltage V_DC Resulting DC Offset Time (T) Voltage
Diagram Description: The section involves voltage waveforms and time-domain behavior in AC switching, which is highly visual.

6. Key Parameters for Selection

6.1 Key Parameters for Selection

Load Voltage and Current Ratings

The load voltage (VLOAD) and current (ILOAD) ratings define the operational limits of a solid-state relay (SSR). Exceeding these values risks thermal runaway or dielectric breakdown. For AC applications, the root-mean-square (RMS) voltage must be considered, while for DC, the peak voltage must not surpass the SSR's maximum blocking voltage. The load current must account for inrush conditions, particularly in inductive or capacitive loads, where transient currents can exceed steady-state values by an order of magnitude.

$$ P_{\text{dissipated}} = I_{\text{LOAD}}^2 \cdot R_{\text{ON}} $$

where RON is the on-state resistance of the SSR. This power dissipation must be managed via heatsinking to avoid junction temperature exceedance.

Control Characteristics

The input control parameters include trigger voltage (VTRIG) and current (ITRIG), typically ranging from 3–32 VDC for voltage and 5–20 mA for current. Optically isolated SSRs often require minimal input power, while transformer-coupled variants may demand higher drive currents. The turn-on and turn-off times, typically in the microsecond to millisecond range, are critical for phase-controlled or high-frequency switching applications.

Thermal Management

The junction-to-case thermal resistance (θJC) and maximum junction temperature (TJ) dictate heatsink requirements. Forced air cooling or passive heatsinks may be necessary for high-current SSRs. The derating curve, which plots permissible load current against ambient temperature, must be consulted for reliable operation.

$$ T_J = T_A + (P_{\text{dissipated}} \cdot \theta_{JA}) $$

where TA is ambient temperature and θJA is the junction-to-ambient thermal resistance.

Isolation Voltage

The isolation voltage rating (VISO) specifies the dielectric strength between input and output, typically 2.5–6 kVRMS. This is critical for safety in high-voltage applications, such as industrial motor drives or medical equipment.

Switching Speed and Frequency

Zero-crossing SSRs minimize inrush currents in resistive loads but introduce a delay of up to half a cycle (8.3 ms at 60 Hz). Random-turn-on SSRs are preferred for phase-angle control or PWM applications. The switching frequency limit, often 1–100 Hz for electromechanical relays, can exceed 1 kHz for SSRs with fast semiconductor switches.

Protection Features

Integrated features like overvoltage protection (MOVs or snubber circuits) and overcurrent protection (e.g., I2t fusing) enhance reliability. SSRs driving inductive loads require freewheeling diodes or RC snubbers to suppress voltage transients during turn-off.

Package and Mounting

SSRs are available in PCB-mount (DIP, SMD), panel-mount, or DIN-rail configurations. The choice depends on thermal dissipation needs, creepage/clearance requirements, and mechanical constraints. Industrial-grade SSRs often feature screw terminals for high-current lugs, while compact SSRs prioritize space efficiency.

6.2 Wiring and Mounting Best Practices

Electrical Isolation and Noise Immunity

Solid-state relays (SSRs) provide galvanic isolation between control and load circuits, typically rated between 2.5 kV and 6 kV. However, improper wiring can compromise this isolation. To minimize capacitive coupling and electromagnetic interference (EMI), maintain a minimum clearance of 5 mm between high-voltage and low-voltage traces on PCBs. For chassis-mounted SSRs, use shielded cables with the shield grounded at a single point to avoid ground loops.

$$ C_{stray} = \frac{\varepsilon_0 \varepsilon_r A}{d} $$

Where \( C_{stray} \) is the parasitic capacitance, \( \varepsilon_0 \) is the permittivity of free space, \( \varepsilon_r \) is the relative permittivity of the insulating material, \( A \) is the overlapping area of conductors, and \( d \) is the separation distance.

Thermal Management

SSRs dissipate power as heat during conduction, given by:

$$ P_{diss} = I_{load}^2 R_{on} + V_{drop} I_{load} $$

Where \( I_{load} \) is the load current, \( R_{on} \) is the on-state resistance, and \( V_{drop} \) is the forward voltage drop. For reliable operation, mount the SSR on a heatsink with thermal resistance \( R_{th} \) satisfying:

$$ T_j = T_a + P_{diss} (R_{th,j-c} + R_{th,c-s} + R_{th,s-a}) < T_{j,max} $$

Here, \( T_j \) is the junction temperature, \( T_a \) is ambient temperature, and \( R_{th,j-c} \), \( R_{th,c-s} \), and \( R_{th,s-a} \) are thermal resistances from junction-to-case, case-to-sink, and sink-to-air, respectively.

Wiring Practices

Mechanical Mounting

SSRs should be mounted in an orientation that promotes convective cooling, typically with the heatsink fins vertical. Avoid mounting near heat sources or in enclosed spaces without forced airflow. For DIN rail mounting, ensure proper engagement of the rail clip and use spacers if stacking multiple relays to prevent overheating.

Torque Specifications

Terminal screws must be tightened to the manufacturer's specified torque (typically 0.5–0.6 N·m for M3 screws). Overtightening can damage the internal PCB, while undertightening increases contact resistance, leading to localized heating.

Grounding Considerations

The SSR case must be bonded to the system ground plane using a low-impedance connection. For high-frequency noise suppression, use a star grounding point and avoid daisy-chaining ground wires. The ground wire cross-section should match or exceed the load current rating.

Safety and Compliance

Verify that the SSR's insulation system meets relevant standards (e.g., UL 508, IEC 62314). Double insulation is required for medical or hazardous location applications. Always include a fast-acting fuse or circuit breaker rated at 150% of the SSR's maximum load current.

6.3 Protection Circuits and Safety Measures

Transient Voltage Suppression

Solid-state relays (SSRs) are susceptible to voltage transients, which can originate from inductive load switching, electrostatic discharge (ESD), or lightning-induced surges. A transient voltage suppressor (TVS) diode or metal-oxide varistor (MOV) is typically placed across the SSR output terminals to clamp excessive voltages. The selection criteria for a TVS diode include:

$$ V_C = V_{BR} + R_D \cdot I_{PP} $$

where \( R_D \) is the dynamic resistance of the TVS diode. For inductive loads, an RC snubber circuit is often added in parallel to dampen high-frequency ringing.

Overcurrent Protection

SSRs lack inherent current-limiting capability, making them vulnerable to short-circuit faults. A fast-acting fuse or electronic current limiter must be employed. The fuse's I²t rating must be lower than the SSR's surge withstand capability to ensure timely interruption. For precise protection, a crowbar circuit using a silicon-controlled rectifier (SCR) can be triggered when current exceeds a threshold:

$$ I_{trip} = \frac{V_{gate}}{R_{sense}} $$

where \( V_{gate} \) is the SCR trigger voltage and \( R_{sense} \) is a shunt resistor.

Thermal Management

Junction temperature directly impacts SSR reliability. The thermal resistance (θJA) from junction to ambient must be minimized via:

Zero-Crossing vs. Random Turn-On

For AC loads, zero-crossing SSRs reduce inrush current but are unsuitable for phase-controlled dimming. In such cases, a random-turn SSR with a fast-acting fuse and MOV is preferred. The trade-off between switching losses and EMI must be evaluated.

Isolation and Grounding

Optocoupler-based SSRs provide galvanic isolation, but improper grounding can compromise safety. A Faraday shield between primary and secondary circuits reduces capacitive coupling, while a ground fault interrupter (GFI) detects leakage currents exceeding 5 mA.

MOV TVS Fuse

For high-voltage applications (>1 kV), reinforced isolation with creepage distances ≥8 mm is mandated by IEC 62368-1.

SSR Protection Circuit Configuration Schematic diagram of a Solid State Relay (SSR) with protection components (TVS diode, MOV, fuse) connected in parallel across the output terminals, showing load and power connections. SSR Fuse (I²t) Load TVS (V_BR, V_C) MOV AC Power AC Neutral
Diagram Description: The section covers multiple protection circuits (TVS, MOV, fuse) and their spatial arrangement relative to the SSR, which is easier to understand visually than textually.

7. Recommended Books and Articles

7.1 Recommended Books and Articles

7.2 Technical Datasheets and Manufacturer Guides

7.3 Online Resources and Tutorials