
Two-function-signal-generator
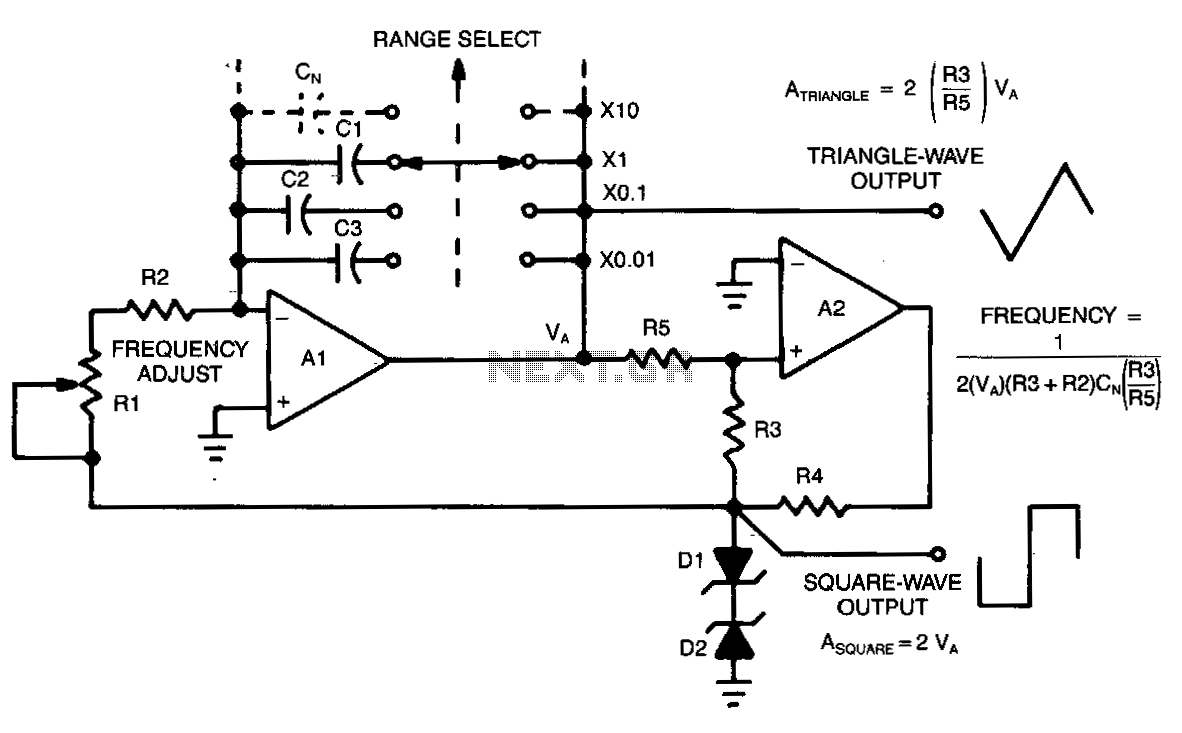
This circuit allows for continuous variation of the frequencies of the triangle and square waves produced, covering a full decade. When the resistance of RS is approximately equal to R3, the amplitudes of the two waveforms will be equal (A_SQUARE = A_TRIANGLE).
The described circuit is likely based on a function generator or oscillator design that utilizes operational amplifiers or comparators to produce triangle and square wave outputs. The frequency variation over a decade indicates a wide range of operational capability, suggesting the use of a variable resistor or a digital potentiometer to fine-tune the frequency settings.
The triangle wave is typically generated through a charging and discharging capacitor connected to a resistor, where the time constant of the RC network defines the frequency of oscillation. The square wave is derived from the triangle wave through a comparator circuit, which flips the output state when the triangle wave crosses a certain threshold.
In the scenario where RS is approximately equal to R3, it indicates a balanced configuration that ensures equal amplitude outputs for both waveforms. This can be critical in applications requiring synchronization of signals, such as in modulation schemes or waveform synthesis.
Additional components may include capacitors for filtering, diodes for clamping, and possibly an op-amp for buffering the output signals. The circuit should also be designed to accommodate load variations without significant distortion to maintain the integrity of the waveforms.
Overall, this circuit's design emphasizes versatility in frequency modulation while ensuring amplitude consistency, making it suitable for various applications in signal processing and waveform generation.You can continuously vary the frequencies of the triangle and square waves produced by this circuit over a full decade. If RS ~ R3, the amplitude of the two waveforms will be equal (A sQUARE= A TRIANGLE). 🔗 External reference
The described circuit is likely based on a function generator or oscillator design that utilizes operational amplifiers or comparators to produce triangle and square wave outputs. The frequency variation over a decade indicates a wide range of operational capability, suggesting the use of a variable resistor or a digital potentiometer to fine-tune the frequency settings.
The triangle wave is typically generated through a charging and discharging capacitor connected to a resistor, where the time constant of the RC network defines the frequency of oscillation. The square wave is derived from the triangle wave through a comparator circuit, which flips the output state when the triangle wave crosses a certain threshold.
In the scenario where RS is approximately equal to R3, it indicates a balanced configuration that ensures equal amplitude outputs for both waveforms. This can be critical in applications requiring synchronization of signals, such as in modulation schemes or waveform synthesis.
Additional components may include capacitors for filtering, diodes for clamping, and possibly an op-amp for buffering the output signals. The circuit should also be designed to accommodate load variations without significant distortion to maintain the integrity of the waveforms.
Overall, this circuit's design emphasizes versatility in frequency modulation while ensuring amplitude consistency, making it suitable for various applications in signal processing and waveform generation.You can continuously vary the frequencies of the triangle and square waves produced by this circuit over a full decade. If RS ~ R3, the amplitude of the two waveforms will be equal (A sQUARE= A TRIANGLE). 🔗 External reference