clock-synchronised multiplexers

This is the second part of the square root algorithm. It was developed during the final stages of finishing this website and reviewing this document for publication. While Part I focused on an empirical discovery for a sequential algorithm to find the square root and its subsequent mathematical proof, Part II addresses a binary search variation that significantly enhances the calculation speed of the root, although the sequential search algorithm remains the smallest available if size is a priority. Both algorithms maintain the same accuracy.

It is important to note that the official address for this document may change without notice. As of August 2000, there is no confirmation of these algorithms being in use, particularly the binary search version. A binary search operates similarly to searching for a word in a dictionary. Instead of starting from the first page, the search takes advantage of the alphabetical order of the words. For example, to find "Green," one would open the dictionary in half, compare the first word found to the target word, and if not a match, divide one of the halves further based on the alphabetical position.

This concept is akin to the childhood game "Simon Says," where one guesses a number between 1 and 100 with limited attempts, using feedback to narrow down possibilities. The optimal strategy mirrors a binary search: beginning with a guess of 50 and halving the range based on whether the guess is too high or too low. This method guarantees finding the number in fewer than eight attempts.

For the square root algorithm, a similar approach is used since both the square root and squaring operations are continuous and ordered. The process begins at half the maximum root that can be calculated. For n-bit numbers, this is represented as follows: for n=16, half of the maximum root is 128. Depending on how the original value (x) compares to the square of 128, one can then halve either the lower or upper section.

For instance, if the lower half is selected, the next comparison would be with the square of 64, while if the upper half is chosen, it would be with the square of 192. The values can be derived by either adding or subtracting one-quarter of the maximum root. As the process continues, one-eighth of the maximum root (32) is used, followed by one-sixteenth (16), and so forth.

The simplest way to determine the next value for comparison is to either add or subtract these maximum root partial values from the current value. For example, if the current value is 192 and x is less than the square of 192, the next comparison would be with the square of 192-32, or 160. This method allows for efficient calculation of the squares of these powers of 2 through right shifts, similarly enabling the calculation of their square roots by halving the maximum root values.

This systematic approach ensures rapid convergence towards the square root, optimizing performance significantly compared to sequential methods. The binary search variation not only maintains accuracy but also enhances computational efficiency, making it a valuable algorithm for applications requiring rapid square root calculations.This is the second part of the square root algorithm. It was developed in one month during the final stages of finishing this web site and reviewing this document for publication. While Part I dealt with an empirical discovery for a sequential algorithm to find the square root, and its subsequent mathematical proof, Part II deals with a binary sea

rch variation that greatly improves the root`s calculation speed (even though the sequential search algorithm is the smallest you`ll find, if size is what matters to you). Both algorithms have the same accuracy. NOTES: The "official" address for this document is. Please do not link directly to the address that shows up in your browser - this may be changed without notice.

Also note that at the time I write this (August 2000) I am not aware of these algorithms being in use (at least the binary search version), but I cannot confirm this. A binary search works pretty much like searching for a word in a dictionary. When looking for "Green", you don`t open the dictionary in the first page and start looking for your word throughout.

Instead you take advantage in the knowledge that the words are ordered alphabetically. Here`s how you would describe the search to someone else: First open the dictionary in half, and look for the first word you find. Compare it to the word you`re looking for. If it`s a match, you found it. Otherwise divide one of the two halves of the dictionary in half again (the right half if the word you`re looking for is after the one you found, the left half if it`s before, alphabetically), and repeat the process.

Remember the game "Simon Says" from childhood "Simon Says: Guess the Number". "I`m thinking of a number between 1 and 100 - guess what it is in under 10 attempts". "I can only tell you if your guess is above or bellow the number I`m thinking of". The best strategy to win at this game is exactly the same. You start by guessing 50, and then go on to guess half of that, then half and so on, based on the answers you get. If you do this you will always get the number in under 8 attempts! This is called a binary search. For the square root algorithm, we can do a similar job (because both the square root and raising to the square are continuous growing operations, and are therefore "ordered"): first start at half the maximum root that can be calculated.

For n-bit numbers, this is For example, for n=16, half of the maximum root is 128. Depending on how the original value to root, x, compares to the square of 128, you cut one of the two halves in half again. One-quarter of the maximum root (or half of 128) is 64, so if you should select the lower half, you compare x with the square of 64, if you select the upper half, you compare x with the square of 192.

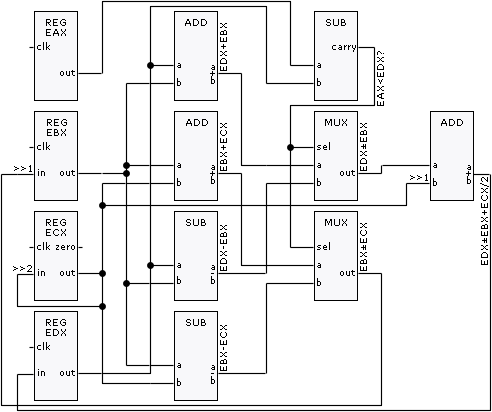
Since 64 is precisely in the middle of the lower half, it can be obtained by either 0+64 or 128-64, and since 192 is precisely in the middle of the upper half, it can be obtained by either 128+64 or 256-64 (i. e. , you get these values by adding one-fourth of the maximum root to the bottom edge of the half, or subtracting it from the top edge of the half, as can be seen in the following graphic).

When you want to split the next quarter in half, you`ll need to use one-eighth of the maximum root (32). On the next step, one-sixteenth (16) and so on. The easiest way to get the value (half of the section you want to move to) from these maximum root partial values, is to add them to the current value (if you want the upper section), or subtract them from it (if you want the lower section).

For instance, if you had moved to 192, and x was now lower than the square of 192, then the next value you want to compare x with is the square of 192-32, or 160. which means that the square of these powers of 2 can be calculated consecutively by shifting the first square twice to the right, just as their square root (the halves of the maximum root) can be calculated by shifting

🔗 External reference