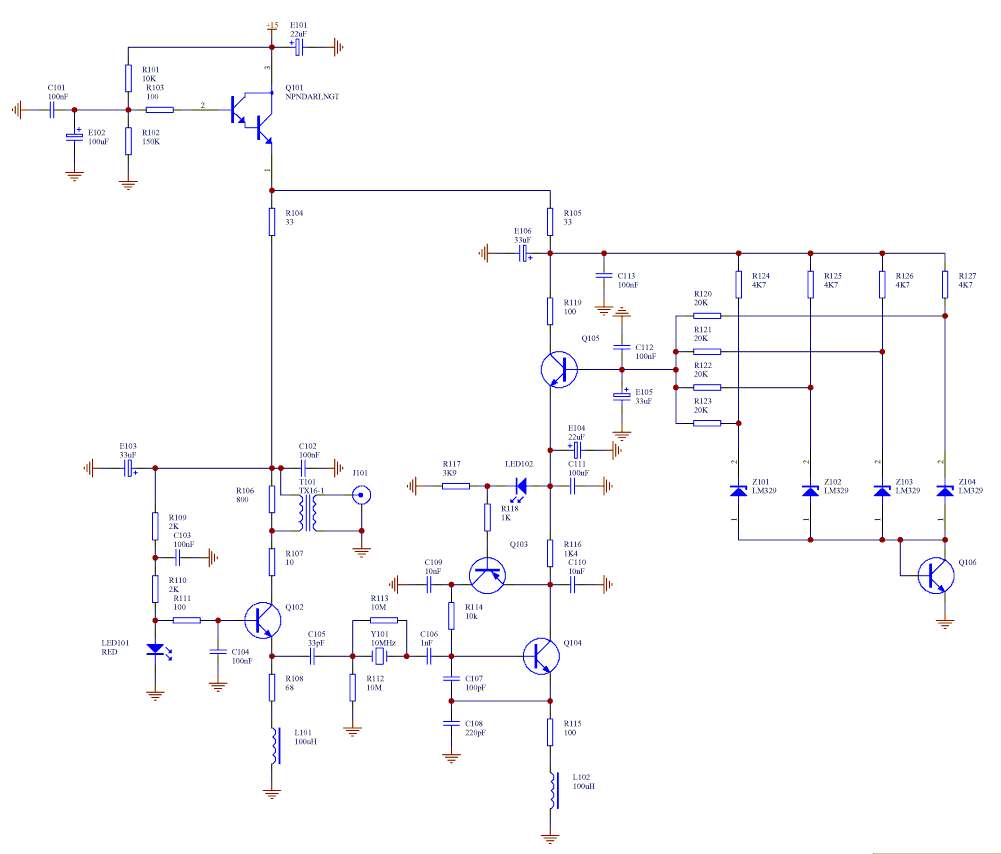
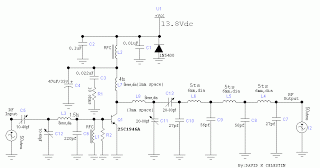
oscillation Oscillator circuit

The first thing to understand is how capacitor C1 is related to the resonance frequency f of the circuit. It appears that selecting a frequency allows for the automatic determination of the necessary value for C1. There are uncertainties regarding whether the circuit functions as a Colpitts or Hartley oscillator, and if the established formulas can be applied, as well as how to implement them in the circuit.

In electronic oscillators, the relationship between capacitance and resonance frequency is crucial. In a Colpitts oscillator, the resonance frequency is determined by the inductance (L) and the equivalent capacitance (Ceq) formed by the capacitors in the circuit, which typically include C1 and another capacitor in series or parallel. The formula for the resonance frequency (f) is given by:

f = 1 / (2π√(L * Ceq))

For a Colpitts oscillator, Ceq can be calculated using the formula:

Ceq = (C1 * C2) / (C1 + C2)

where C2 is the additional capacitor in the circuit. By selecting a desired frequency, the appropriate value for C1 can be derived by rearranging this equation, allowing for the calculation of C1 based on the known values of L and C2.

In contrast, a Hartley oscillator also employs inductors and capacitors to generate oscillations, but it typically uses a tapped inductor and a single capacitor for frequency determination. The resonance frequency for a Hartley oscillator is expressed as:

f = 1 / (2π√(L * C))

where L is the total inductance and C is the capacitance in the circuit. To identify whether the circuit is a Colpitts or Hartley oscillator, one must analyze the configuration of the components. If the circuit features two capacitors in a specific arrangement, it is likely a Colpitts oscillator. If it has a tapped inductor with a single capacitor, it is likely a Hartley oscillator.

Understanding the configuration and applying the appropriate formulas will clarify the relationship between C1 and the resonance frequency, enabling effective design and implementation of the oscillator circuit.The first thing I need to know how C1 is related to resonance frequency f of the circuit. It seems like I can choose a frequency and I automatically get a needed value for C1. I have a lot of doubts I don`t know if the circuit constitutes a Colpitts or Hartley oscillator and if I can use the known formulas and then how I would apply it my circuit. 🔗 External reference