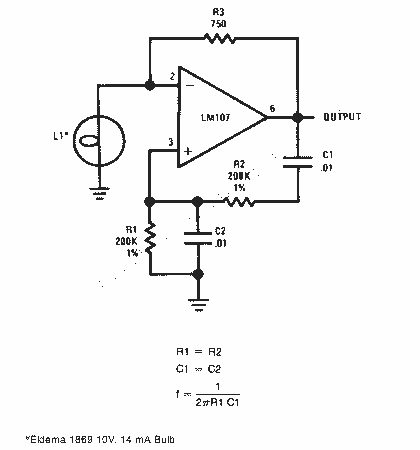
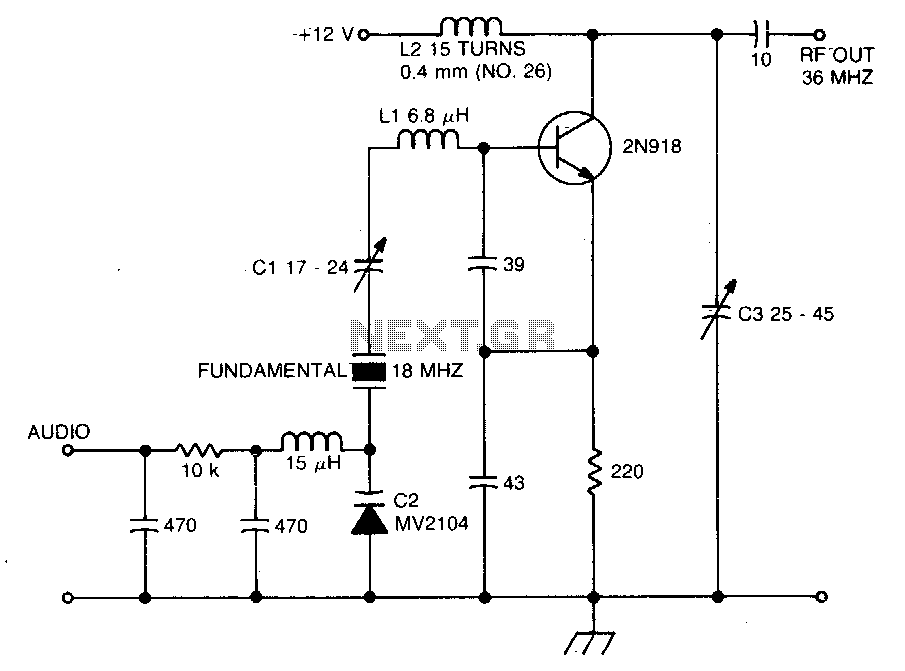
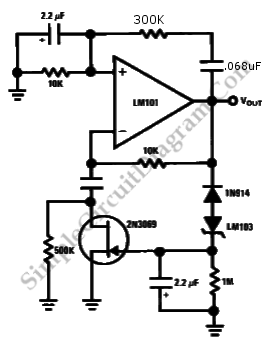
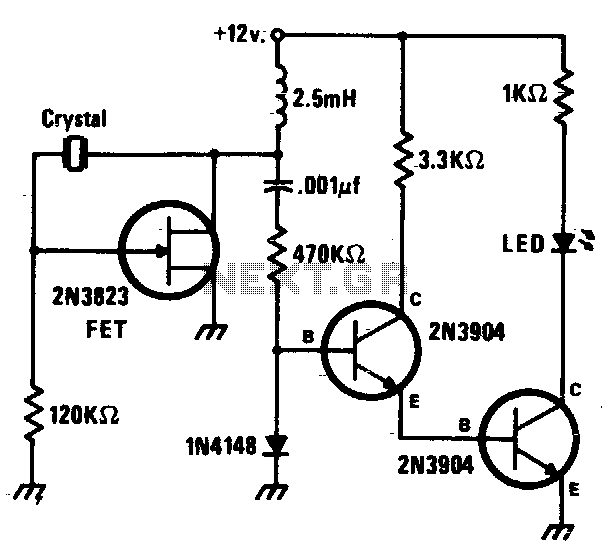
Crystal Oscillator
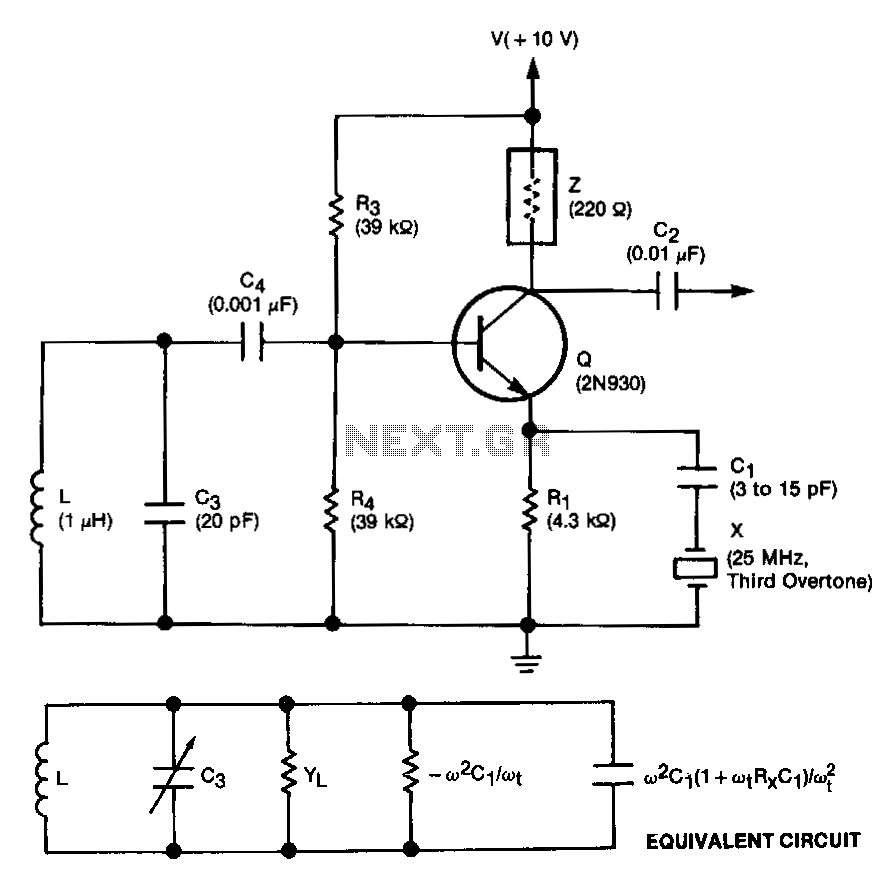
In crystal oscillators, the conventional electrical resonant circuit is substituted by a mechanically vibrating crystal. The crystal, typically made of quartz, maintains a high degree of stability at the frequency for which it is originally cut. Consequently, crystal oscillators are utilized in applications requiring exceptional stability, such as communication transmitters, receivers, and digital clocks. A quartz crystal demonstrates a significant property known as the piezoelectric effect. When mechanical pressure is applied to the crystal's faces, a voltage proportional to the applied pressure is generated across the crystal. Conversely, applying a voltage across the crystal causes it to deform in a manner proportional to the voltage. An alternating voltage applied to the crystal induces vibrations at its natural frequency. Other materials exhibiting the piezoelectric effect include Rochelle salt and tourmaline. While Rochelle salt exhibits the strongest piezoelectric effect, its applications are limited due to its mechanical weakness and sensitivity to moisture and heat. Tourmaline, while more robust, displays the least piezoelectric effect. Quartz strikes a balance between the piezoelectric properties of Rochelle salt and the mechanical strength of tourmaline, making it inexpensive and readily available. It is predominantly used in radio-frequency (RF) oscillators. For electronic oscillator applications, the crystal is precisely cut and mounted between two metal plates. Although the crystal exhibits electro-mechanical resonance, its behavior can be modeled as an electrical resonant circuit. The crystal functions as a series R-L-C circuit in parallel with CM, where CM represents the capacitance of the mounting electrodes. Due to the minimal losses represented by R, the equivalent quality factor (Q) of the crystal is high, typically around 20,000, with values reaching up to 1,000,000 obtainable with specific crystals. The presence of CM results in two resonant frequencies: the series resonant frequency (fs) and the parallel resonant frequency (fp). At fs, the crystal impedance is very low, while at fp, the impedance is very high. The impedance versus frequency characteristics of the crystal illustrate these behaviors. Proper utilization of the crystal requires connecting it in a circuit that selects either its low impedance in the series-resonant operating mode or its high impedance in the anti-resonant or parallel resonant operating mode. The series resonant frequency is given by the expression fs = 1/2π√(LC), while the parallel resonant frequency is described by fp = 1/2π√[1 + C/CM] / √(LC). Although fp is typically higher than fs, the two frequencies are closely spaced due to the small ratio of C to CM. To stabilize the oscillator's frequency, the crystal may operate at either its series or parallel resonant frequency. In the series-resonant mode, the crystal is connected as a series element in a feedback path, resulting in minimal impedance and maximal positive feedback. Resistors R1, R2, and RE form a voltage-divider stabilized DC bias circuit, while capacitor CE provides AC bypass for the emitter resistor R. The radio-frequency coil (RFC) facilitates DC bias while isolating any AC signals on the power lines from influencing the output signal. The voltage feedback signal from the collector to the base is maximized when the crystal impedance is at its lowest.
The crystal oscillator's circuit design is pivotal in achieving frequency stability and performance. The crystal is typically connected in a configuration that allows it to operate in its series-resonant mode, where the impedance is minimized, enhancing the feedback loop's effectiveness. The feedback path is crucial, as it determines the oscillator's gain and stability. The resistors in the biasing network must be carefully selected to ensure that the DC operating point remains stable, preventing drift that could lead to frequency instability.
In addition to the feedback network, careful consideration must be given to the layout of the PCB to minimize parasitic capacitance and inductance, which could affect the oscillator's performance. Shielding may also be necessary to protect the oscillator from external electromagnetic interference, which could influence its frequency stability.
The choice of crystal is also critical; factors such as the cut type (e.g., AT-cut or BT-cut), frequency tolerance, and temperature coefficient need to be evaluated to ensure optimal performance in the intended application. The characteristics of the crystal and the surrounding circuitry ultimately determine the oscillator's ability to maintain a precise frequency over varying environmental conditions.
In summary, the design and implementation of a crystal oscillator require a comprehensive understanding of both the crystal's physical properties and the electrical characteristics of the surrounding circuit. This knowledge is essential for developing reliable and stable oscillators for various electronic applications.In crystal oscillators, the usual electrical resonant circuit is replaced by a mechanically vi brating crystal. The crystal (usually quartz) has a high degree of stability in holding con stant at whatever frequency the crystal is originally cut to operate.
The crystal oscillators are, therefore, used whenever great stability is needed, for examp le, in communication trans mitters, and receivers, digital clocks etc. A quartz crystal exhibits a very important property known as piezo-electric effect. Whena mechanical pressure is applied across the faces of the crystal, a voltage proportional tothe applied mechanical pressure appears across thecrystal. Conversely, when a voltage is applied across the crystal surfaces, the crystal is distorted by an amount proportional to the applied voltage.
An alter nating voltage applied to a crystal causes it to vibrate at its natural frequency. Besides quartz, the other substances that exhibit the piezo-electric effect are Rochelle salt and tourmaline. Rochelle salt exhibits the greatest piezoelectric effect, but its applications are limited to manufacture of microphones, headsets and loudspeakers.
It is because the Rochelle salt is mechanically the weakest and strongly affected by moisture and heat. Tourmaline is most rugged but shows the least piezo-electric effect. Quartz is a compromise between the piezoelectric effect of Rochelle salt and the mechani cal strength of tourmaline.
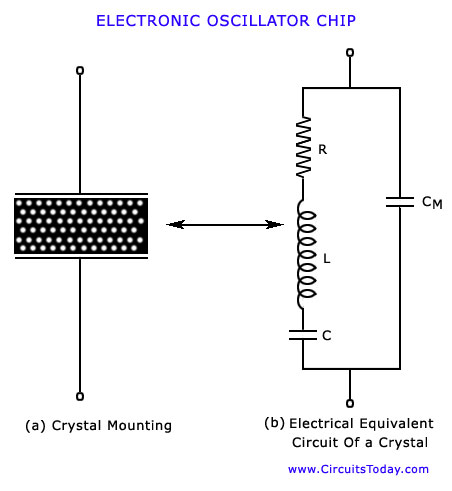
It is inexpensive and readily available in nature. It is mainly the quartz crystal that is used in radio-frequency (RF) oscillators. For use in electronic oscillators, the crystal is suitably cut and then mounted between two metal plates, as shown in fig (a). Although the crystal has electro-mechanical resonance but the crystal action can be represented by an electrical resonance circuit, as shown in fig.
(b). The crystal actually behaves as a series R-L-C circuit in parallel with CM where CM is the capacitance of the mounting electrodes. Because the crystal losses, represented by R, are small the equivalent crystal Q is high-typically 20, 000.
Values of Q upto 106 can be obtained by making use of crystals. Because of presence of CM, the crystal has two resonant fre quencies. One of these is the series resonant frequency fs at which2 fL = 1/2 fCand in this case the crystal impedance is verylow. The other is parallel resonance frequency fp which is dueto parallel resonance of capacitance CM and the reactance of the series circuit.
In this case crystal impedance is very high. The impedance versus frequency curve of the crystal is shown in figure. In order to use the crystal properly it must be connected in a circuit so that its low impedance in the series-resonant op erating mode or high impedance in the anti-resonant or paral lel resonant operating mode is selected. Two resonant frequencies are given by the expressionsSeries resonant frequency, fs = 1/2 LC Parallel resonant frequency, FP = 1/2 [1 + C/CM] / LC It appears that fp is higher than fs but the two frequencies are very close to each other.
It is due to the fact that the ratio C/CM is very small. To stabilize the frequency of an oscillator, a crystal may be operated at either its series or parallel resonant frequency. To excite a crystal for operation in the series-resonant mode it may be connected as a series element in a feedback path, as shown in figure.
In this mode of operation the crystal impedance is the smallest and the amount of positive feedback is the largest. Resistor R1, R2 and RE provide a voltage-divider stabilized dc bias circuit, the capacitor CE provides ac bypass of the emitter resistor R and the radio-frequency coil (RFC) provides for dc bias -while decoupling any ac signal on the power lines from affecting the output signal.
The voltage feedback sigrTal from the collector to the base is maximum when the crystal impedance i 🔗 External reference
The crystal oscillator's circuit design is pivotal in achieving frequency stability and performance. The crystal is typically connected in a configuration that allows it to operate in its series-resonant mode, where the impedance is minimized, enhancing the feedback loop's effectiveness. The feedback path is crucial, as it determines the oscillator's gain and stability. The resistors in the biasing network must be carefully selected to ensure that the DC operating point remains stable, preventing drift that could lead to frequency instability.
In addition to the feedback network, careful consideration must be given to the layout of the PCB to minimize parasitic capacitance and inductance, which could affect the oscillator's performance. Shielding may also be necessary to protect the oscillator from external electromagnetic interference, which could influence its frequency stability.
The choice of crystal is also critical; factors such as the cut type (e.g., AT-cut or BT-cut), frequency tolerance, and temperature coefficient need to be evaluated to ensure optimal performance in the intended application. The characteristics of the crystal and the surrounding circuitry ultimately determine the oscillator's ability to maintain a precise frequency over varying environmental conditions.
In summary, the design and implementation of a crystal oscillator require a comprehensive understanding of both the crystal's physical properties and the electrical characteristics of the surrounding circuit. This knowledge is essential for developing reliable and stable oscillators for various electronic applications.In crystal oscillators, the usual electrical resonant circuit is replaced by a mechanically vi brating crystal. The crystal (usually quartz) has a high degree of stability in holding con stant at whatever frequency the crystal is originally cut to operate.
The crystal oscillators are, therefore, used whenever great stability is needed, for examp le, in communication trans mitters, and receivers, digital clocks etc. A quartz crystal exhibits a very important property known as piezo-electric effect. Whena mechanical pressure is applied across the faces of the crystal, a voltage proportional tothe applied mechanical pressure appears across thecrystal. Conversely, when a voltage is applied across the crystal surfaces, the crystal is distorted by an amount proportional to the applied voltage.
An alter nating voltage applied to a crystal causes it to vibrate at its natural frequency. Besides quartz, the other substances that exhibit the piezo-electric effect are Rochelle salt and tourmaline. Rochelle salt exhibits the greatest piezoelectric effect, but its applications are limited to manufacture of microphones, headsets and loudspeakers.
It is because the Rochelle salt is mechanically the weakest and strongly affected by moisture and heat. Tourmaline is most rugged but shows the least piezo-electric effect. Quartz is a compromise between the piezoelectric effect of Rochelle salt and the mechani cal strength of tourmaline.
It is inexpensive and readily available in nature. It is mainly the quartz crystal that is used in radio-frequency (RF) oscillators. For use in electronic oscillators, the crystal is suitably cut and then mounted between two metal plates, as shown in fig (a). Although the crystal has electro-mechanical resonance but the crystal action can be represented by an electrical resonance circuit, as shown in fig.
(b). The crystal actually behaves as a series R-L-C circuit in parallel with CM where CM is the capacitance of the mounting electrodes. Because the crystal losses, represented by R, are small the equivalent crystal Q is high-typically 20, 000.
Values of Q upto 106 can be obtained by making use of crystals. Because of presence of CM, the crystal has two resonant fre quencies. One of these is the series resonant frequency fs at which2 fL = 1/2 fCand in this case the crystal impedance is verylow. The other is parallel resonance frequency fp which is dueto parallel resonance of capacitance CM and the reactance of the series circuit.
In this case crystal impedance is very high. The impedance versus frequency curve of the crystal is shown in figure. In order to use the crystal properly it must be connected in a circuit so that its low impedance in the series-resonant op erating mode or high impedance in the anti-resonant or paral lel resonant operating mode is selected. Two resonant frequencies are given by the expressionsSeries resonant frequency, fs = 1/2 LC Parallel resonant frequency, FP = 1/2 [1 + C/CM] / LC It appears that fp is higher than fs but the two frequencies are very close to each other.
It is due to the fact that the ratio C/CM is very small. To stabilize the frequency of an oscillator, a crystal may be operated at either its series or parallel resonant frequency. To excite a crystal for operation in the series-resonant mode it may be connected as a series element in a feedback path, as shown in figure.
In this mode of operation the crystal impedance is the smallest and the amount of positive feedback is the largest. Resistor R1, R2 and RE provide a voltage-divider stabilized dc bias circuit, the capacitor CE provides ac bypass of the emitter resistor R and the radio-frequency coil (RFC) provides for dc bias -while decoupling any ac signal on the power lines from affecting the output signal.
The voltage feedback sigrTal from the collector to the base is maximum when the crystal impedance i 🔗 External reference
Related Circuits
Incandescent lamp has been used to reduce harmonic distortion in sine oscillator circuit. The nonlinear resistance characteristic of the lamp filament help the circuit to shape the signal to approximate the ideal sine wave. Here is the classic Wien-bridge...
The crystal operates into a complex load at series resonance. L1, C1, and C2 balance the crystal at zero reactance. Capacitor C1 fine-tunes the center frequency. A tank circuit consisting of L2 and C3 doubles the output frequency, allowing...
Achieving the appropriate amplifier loop gain is a significant challenge in generating a low distortion, constant amplitude sine wave. Nevertheless, this issue can be addressed with... Amplifier loop gain is a critical parameter in the design of audio and signal...
This circuit is a simple Pierce oscillator with an LED go/no-go display. The checker works best with crystals having fundamental frequencies in the seven to eight megahertz range. The Pierce oscillator circuit is a popular choice for generating high-frequency signals,...
This unit is easily tunable and stable, consumes minimal power, and is more cost-effective than other types of oscillators that operate at similar frequencies. This unique combination of features is made possible by a design concept that involves operating...
The Hartley Oscillator is an LC oscillator that derives its feedback from magnetically coupled energy in a tapped coil. Hartley oscillators are inductively coupled variable frequency oscillators. The Hartley Oscillator is a type of electronic oscillator that utilizes an inductor-capacitor...