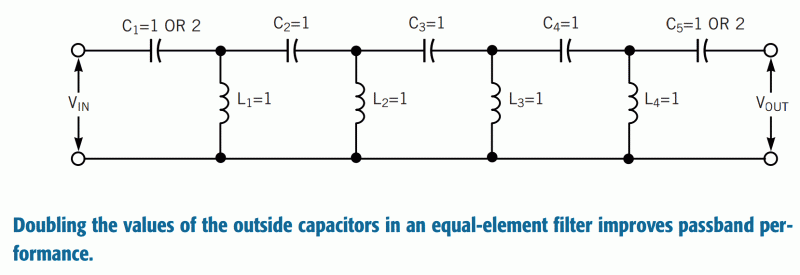
active filters

There is a class of filter known as "all-pass" that does not alter the amplitude response but only the phase. Although this may initially seem insignificant, like many circuits developed over the years, it can be quite useful. Filters also influence the transient response of the signal that passes through them, and extreme filters (high-order types or filters with a high Q factor) can induce ringing (a damped oscillation) at the filter's cutoff frequency. This ringing may not pose a problem if it occurs outside the audio range; however, it can be problematic for filters used in crossover networks, for example. For those unfamiliar with filter concepts, it is advisable to refer to the article "Designing With Opamps - Part 2," which provides some background information, albeit with less detail than presented here. There is some overlap in content, as the original article was written some time ago, and it was deemed beneficial to include basic information in both articles. Filters are utilized at specific frequencies, necessitating recalculation of the filters described here. The frequency setting components have been normalized to 10k for resistors and 10nF for capacitors, yielding a -3dB frequency of 1.59kHz in most cases. Increasing capacitance or resistance lowers the cutoff frequency, while decreasing them raises it. Capacitors employed in filter circuits should be of polyester, Mylar, polypropylene, polystyrene, or similar types. NP0 (C0G) ceramics may be suitable for low values. The choice of capacitor dielectric should be based on the anticipated use of the filter. Multilayer ceramic capacitors should be avoided in filter applications as they can introduce distortion and are typically highly dependent on voltage and temperature. Electrolytic capacitors, including bipolar and particularly tantalum types, should also be avoided if possible. It is important to note that nearly all filter circuits presented are designed to be fed from a low-impedance source, which must sometimes be earth (ground) referenced. Op-amp power connections, supply bypass capacitors, and pin numbers are not depicted. All circuits are functional as illustrated. Additionally, output "stopper" resistors from op-amp outputs must be included for any signal that exits an op-amp and connects to the outside world via a shielded cable. Most op-amps will oscillate if a resistor is not employed in series with the output pin. A value of 100 ohms is convenient, but it can be lower (resulting in less safety margin) or higher (leading to increased output impedance). The following represents a relatively small sample of the various topologies available, selected for their potential utility. Some of the circuits shown are quite common, while others are less frequently encountered. In discussing filter properties, heavy mathematical analysis has been avoided. The provided mathematical formulas are sufficient to enable filter configuration, as few readers are likely to engage in detailed calculations, which are generally not useful outside of academic settings. Common filter terminology describes the pass-band and stop-band, and may refer to the transition-band, where the filter transitions through the design frequency. The Q factor measures "quality," but not in the conventional sense. A high-Q filter is not inherently "better" than a low-Q design and may be less suitable for many applications. In some instances, the term "damping" is used instead, which is simply the inverse of Q (i.e., 1/Q). The -3dB frequency is defined as the point where the output level has decreased by 3dB from the maximum level within the passband. Therefore, if a filter produces a 1dB peak before rolloff, the -3dB point will be 2dB below the average level.

The all-pass filter is a unique topology in the realm of signal processing. Its primary function is to alter the phase of the input signal without affecting its amplitude, making it particularly useful in various applications such as phase correction in audio systems and in digital signal processing where phase relationships are critical. The all-pass filter can be implemented using operational amplifiers (op-amps) in various configurations, such as first-order or higher-order designs, depending on the required phase shift.

The design of an all-pass filter typically involves selecting appropriate resistors and capacitors to achieve the desired phase response across a specified frequency range. The frequency response can be tailored by adjusting component values, allowing for flexibility in design. The phase shift introduced by the filter can be calculated using the formula derived from the transfer function of the circuit, ensuring that the filter meets the specific requirements of the application.

In practical implementations, attention must be given to the choice of components, particularly the capacitors, as their characteristics can significantly influence the performance of the filter. Using high-quality capacitors, such as polyester or polypropylene, ensures minimal distortion and stable operation across varying temperatures and voltages. Additionally, the design should incorporate provisions for low-impedance sources to prevent oscillations and ensure signal integrity.

Overall, while the all-pass filter may appear straightforward, its applications and implications in signal processing are profound, providing essential phase manipulation capabilities without compromising signal strength. This characteristic makes it an invaluable tool in the toolkit of engineers working in audio, telecommunications, and various other fields that rely on precise signal control.There is one class of filter called "all-pass" that does not affect the response, only phase. While at first look this might be thought rather pointless, like all circuits that have been developed over the years it often comes in very handy. Filters also affect the transient response of the signal passing through, and extreme filters (high order types or filters with a high Q)

can even cause ringing (a damped oscillation) at the filter`s cutoff frequency. In some cases, this doesn`t represent a problem if the ringing is outside the audio band, but can be an issue for filters used in crossover networks (for example). If you are not already familiar with the concept of filters, it might be better to read the article Designing With Opamps - Part 2, as this gives a bit more background information but a lot less detail than shown here.

There is some duplication - the original article was written some time ago, and it was considered worthwhile to include some of the basic info in both articles. Filters are used at the frequencies where they are needed, so the filters described here need to be recalculated.

I have normalised the frequency setting components to 10k for resistors, and 10nF for capacitors. This provides a -3dB frequency of 1. 59kHz in most cases. Increasing capacitance or resistance reduces the cutoff frequency and vice versa. Capacitors used in filter circuits should be polyester, Mylar, polypropylene, polystyrene or similar. NP0 (aka C0G) ceramics can be used for low values. Choose the capacitor dielectric depending on the expected use for the filter. Never use multilayer ceramic caps for filters, because they will introduce distortion and are usually highly voltage and temperature dependent.

Likewise, if at all possible avoid electrolytic capacitors - including bipolar and especially tantalum types. Note Carefully: Nearly all filter circuits shown expect to be fed from a low impedance source, which in some cases must be earth (ground) referenced.

Opamp power connections are not shown, nor are supply bypass capacitors or pin numbers. All circuits are functional as shown. Also not shown are output `stopper` resistors from opamp outputs. These must be included for any signal that leaves an opamp and connects to the outside world using a shielded cable. Most opamps will oscillate if a resistor is not used in series with the output pin. 100 ohms is a convenient value, but it can be lower (less safety margin) or higher (higher output impedance).

The following is actually a fairly small sample of all the different topologies, but the examples have been selected based on their potential usefulness. Some of the circuits shown are extremely common, others less so. In the general discussions about filter properties I have avoided heavy mathematical analysis. The maths formulas provided are enough to allow you to configure the filter - few readers will want to perform detailed calculations and they are not generally useful other than for university exams.

The common terminology of filters describes the pass-band and stop-band, and may refer to the transition-band, where the filter passes through the design frequency. Q is a measure of `quality`, but not in the normal sense. A high-Q filter is not inherently `better` than a low-Q design, and may be much worse for many applications.

In some cases, the term `damping` is used instead, which is simply the inverse of Q (i. e. 1/Q). It is generally defined that the -3dB frequency is the point where the output level has fallen by 3dB from the maximum level within the passband. This means that if a filter produces a 1dB peak before rolloff, the -3dB point is then actually 2dB below the average level.

I tend to disagree that this is the most 🔗 External reference