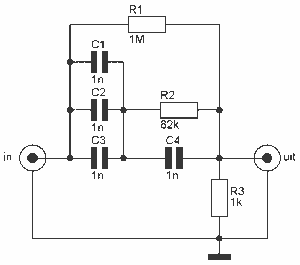
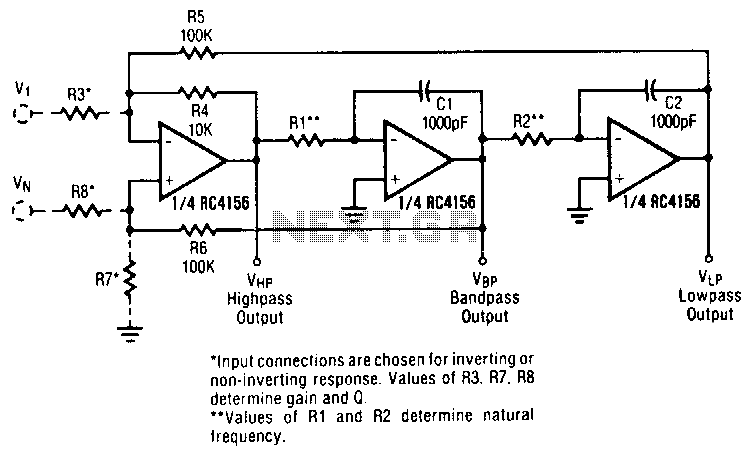
Universal active filter

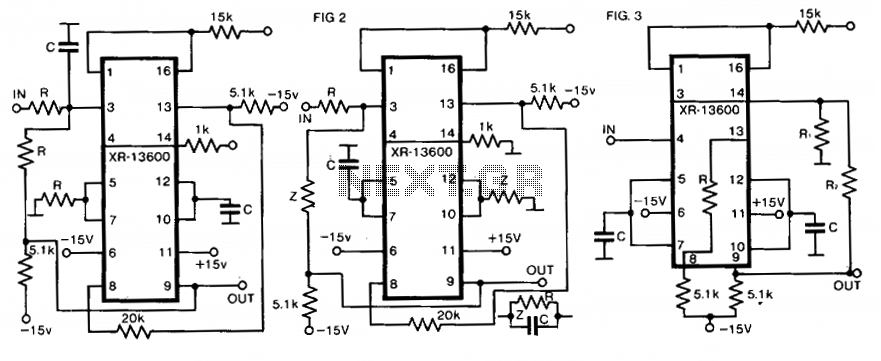
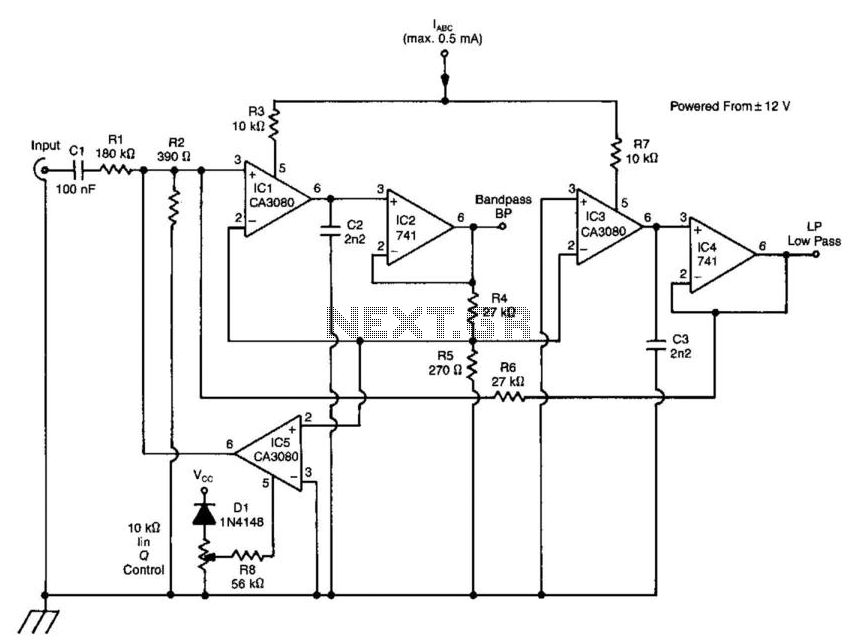
The circuit presented operates as a bandpass filter, with the transfer function derived from FBP(s) = 1 + s/Qo + s²/w₀². The cut-off frequency, denoted as ω₀, and the quality factor (Q-factor) are defined by ω₀ = g/C and Q = gR/2, where g represents the transconductance at room temperature. By swapping the capacitor C with the resistor R at the circuit's input, a high-pass filter operation can be achieved. A low-pass filter configuration can be established by connecting two components in parallel, designated as R and C, as illustrated in Figure 2. The low-pass filter's performance can be significantly enhanced with the circuit design shown in Figure 3. Additionally, the gain and Q-factor can be independently adjusted concerning the cut-off frequency, as indicated by the equations Q = 1/fB = 1 + R₂/R₁, A = Q², and ω₀ = g/C.

The described circuit functions as a versatile filter capable of bandpass, high-pass, and low-pass operations, depending on the configuration of its components. The transfer function highlights the relationship between the input and output signals, revealing how the circuit selectively allows certain frequency ranges to pass while attenuating others.

The cut-off frequency (ω₀) is a critical parameter, determining the point at which the filter begins to attenuate frequencies. It is influenced by the values of the capacitor (C) and the transconductance (g). In practical applications, the transconductance is a measure of how effectively the circuit can convert input voltage changes into output current changes, and it is temperature-dependent.

The Q-factor, a dimensionless parameter, characterizes the selectivity and bandwidth of the filter. A higher Q indicates a narrower bandwidth and more selective filtering, while a lower Q results in a broader bandwidth. The relationship between the Q-factor and the resistor values (R₁ and R₂) allows for fine-tuning of the filter characteristics in real-time applications.

The transition from a bandpass to a high-pass filter by interchanging the capacitor and resistor is a common practice in filter design, allowing for flexibility in circuit applications. The low-pass filter configuration, as indicated in the schematic, emphasizes the role of parallel connections in achieving desired frequency response characteristics.

Overall, the circuit's design can be adapted for various applications, including audio processing, communication systems, and signal conditioning, where control over frequency response is essential. The ability to independently adjust gain and Q-factor provides enhanced control over the circuit's performance, making it suitable for a wide range of electronic applications.The circuit as shown gives the bandpass operation the transfer function calculated from FBP(s) = where = 1 + s/Qo>0 + s2/w02. The cut-off frequency, 0, and the Q-factor are given by 0 = g/C and Q = gR/2 where g is the transconductance at room temperature.

Interchanging the capacitor C with the resistor R at the input of the circuit high-pass operation is obtained. A low-pass filter is obtained by applying two parallel connections ctf R and C as shown in Fig. 2. The low-pass operation may be much improved with the circuit as given in Fig. 3. Here the gain and Q may be set up separately with respect to the cut-off frequency according to the equations Q = 1/fB = 1 + R2/R!, A = Q2 and 0 = g ffi/C.