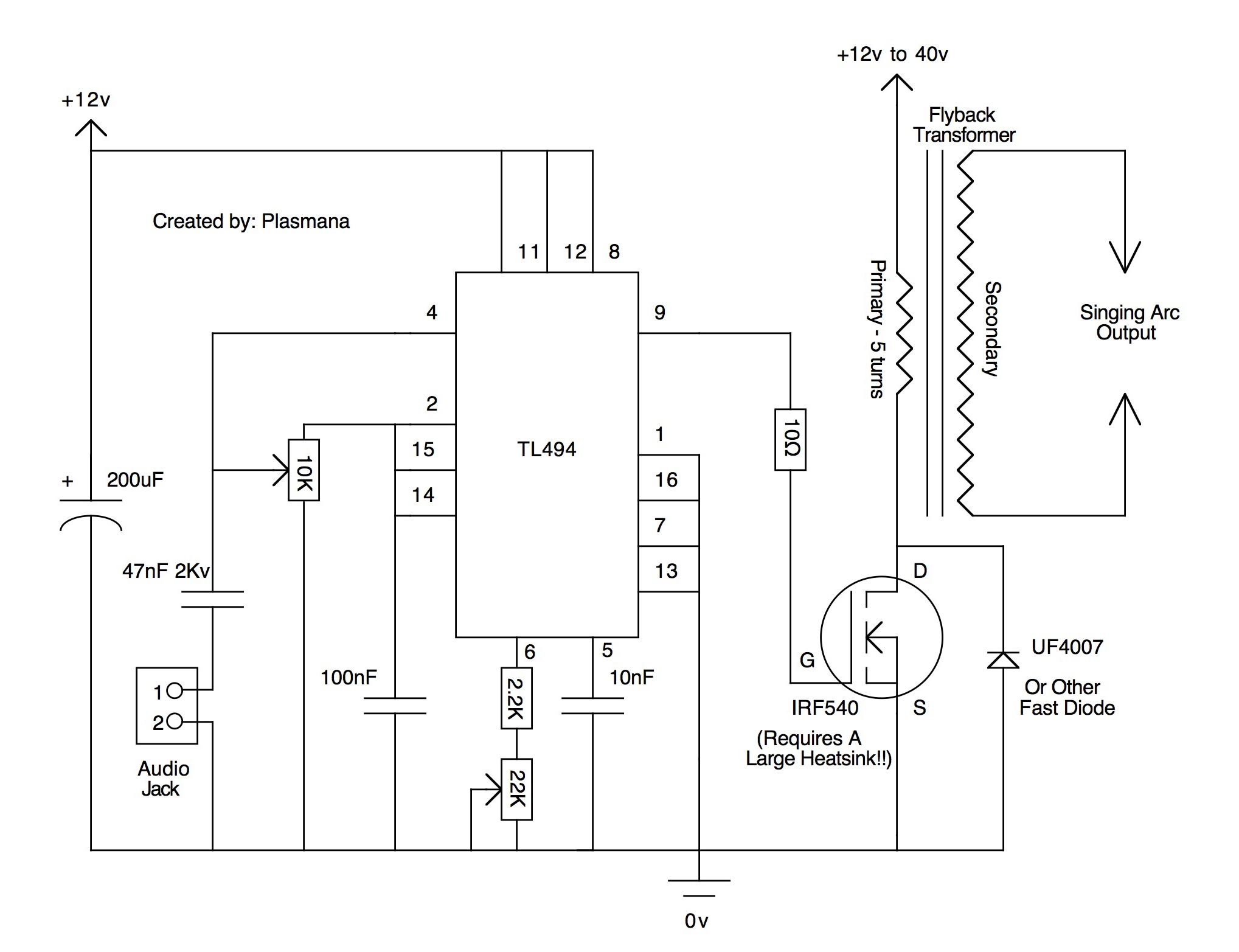
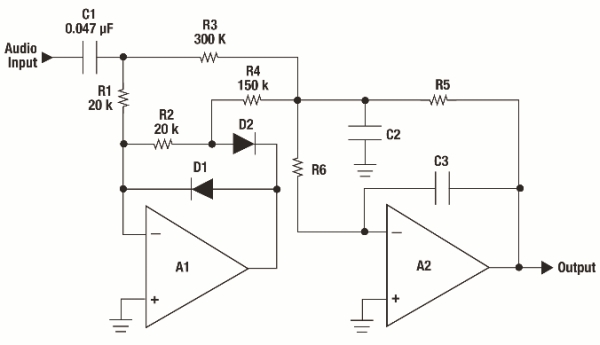
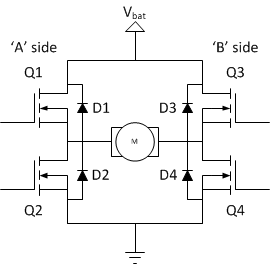
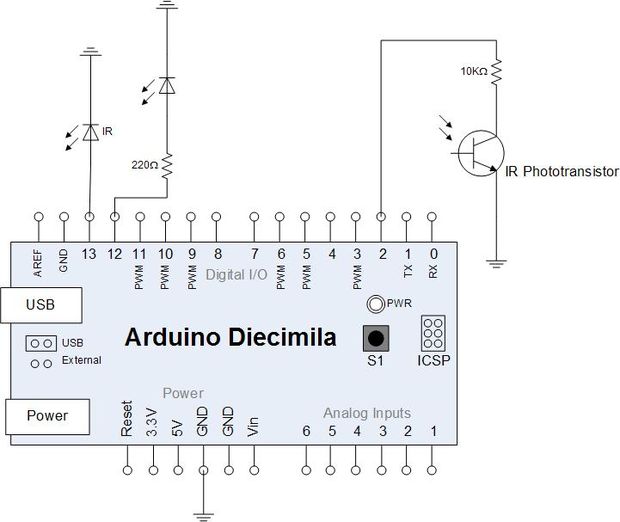
basics of electricity
The study of electricity involves several key terms that explain the behavior of electrical charge. Electrical charge and its related phenomena are fundamental to the world we inhabit. The understanding and application of electricity have significantly contributed to the advanced technologies we enjoy today, including electric light, heating, digital computers, television, CDs, DVDs, radar, microwaves, and mobile phones. The earliest recorded investigations into natural attractive phenomena occurred over 2,500 years ago among the ancient Greeks. In the past few centuries, especially the last century, this understanding has expanded dramatically. Notably, significant advancements were made between 1785 and 1826. The fundamental unit of electric charge is the coulomb, named after French physicist Charles Augustin de Coulomb. A single electron, a subatomic particle, carries a minuscule amount of charge, approximately 1.6 x 10^-19 coulombs. Consequently, one coulomb of electric charge corresponds to about 6.25 x 10^18 electrons. To illustrate, if each electron were the size of a marble, they could stretch from the Earth to the moon and back over 100 million times.
A collection of stationary electric charges signifies stored or potential electrical energy, which can be quantified by voltage. The unit of electrical potential is the volt, named after Italian physicist Alessandro Volta. Discussions of electric charge movement are typically framed from the perspective of positive charges. It is essential to note that while individual electrons possess a negative charge, most electronic manuals and instruments indicate positive charge concentrations or flows. Electric charges move from higher to lower voltage, akin to marbles rolling down a hill. The movement of charge is governed by the electrical potential and the resistance of the conductive path. The unit of resistance is the ohm, named after German physicist George Simon Ohm. When electric charge moves, it generates an electric current, which is the most familiar form of electricity. The size of the electric current, measured in amperes, corresponds to the quantity of charge passing a reference point over time.
The relationship between volts, amps, and ohms is vital for understanding electricity. An electric circuit, which comprises conductive paths, allows charge movement when closed, while an open circuit does not. Voltage, essential for driving charge through a circuit, must be sufficient and correctly polarized. Ohm's Law defines the relationship between current, voltage, and resistance, expressed mathematically as I = V/R. Kirchoff's laws further govern voltage and current distribution in complex circuits.
To understand electrical potential and charge motion, analogies to gravitational potential and fluid motion can be useful, though they have limitations. The speed of charge movement is nearly constant, approaching the speed of light. In typical circuits, all components become energized almost instantaneously. The analogy of fluid motion can be employed to compare water pressure with voltage, although it can be misleading in certain contexts.
In terms of circuit representation, batteries are depicted with long and short horizontal lines indicating individual cells, with pairs of lines representing the voltage of the battery.
In summary, the study of electricity encompasses the exploration of charge behavior and its implications for technology, governed by fundamental principles such as Ohm's Law and Kirchoff's laws. Understanding these concepts is crucial for the design and analysis of electrical circuits and systems.The study of electricity revolves around a few common terms that describe the behavior of electrical charge. Electrical charge and its associated phenomena are a fundamental part of the world that we live in. The understanding and use of electricity is largely responsible for the advanced technology that we enjoy today: electric light, heat, digit
al computers, television, music on CD, DVD video, radar, microwave ovens, cell phones, and on and on and on. The first recorded studies of natural attractive phenomena occurred among the ancient Greeks over 2, 500 years ago.
That`s right, over 2 thousand 5 hundred years ago. Over the last 2 or 3 hundred years, and particularly in the last century, that understanding has grown tremendously. In fact, some of the most interesting work relative to this limited discussion was done over a 40-year span between 1785 and 1826.
The fundamental unit of electric charge is the COULOMB, named for Charles Augustin de Coulomb, a French physicist (1736-1806). The smallest concentration of charge is contained in a single electron, a subatomic particle. The Coulomb is an extremely large amount of charge, or stated more precisely, an electric charge equal to 1 Coulomb requires an extremely large number of electrons.
The charge of a single electron is 0. 00000000000000000016 Coulombs. That`s 18 zeros in front of the 16. Stated in the notation that scientists prefer, called coincidentally, scientific notation, that amount of charge would be 1. 6 x 10-19 Coulombs. So 1 Coulomb of electric charge represents 6. 25 x 1018 electrons or 6, 250, 000, 000, 000, 000, 000 electrons. That`s a whole bunch of electrons (6. 25 billion billion or if you prefer 6. 25 million trillion). In fact, if each electron was a large as a marble, with a ½ inch diameter, you could line them up end to end in a straight line and reach from the earth to the moon and back over 100 million times.
So what do we know about electric charge except that the charge on a single electron is pretty small A collection of electric charges standing still represents an amount of stored, or potential electrical energy. A more convenient way to look at the stored electrical energy within a collection of electric charges standing still is the potential ability for the electric charges to move.
In this context we speak about an electrical potential , described numerically or quantified by an amount of voltage. The fundamental unit of electrical potential is the VOLT, named for Alessandro Volta, an Italian physicist (1745-1827).
To avoid the inevitable confusion resulting from trying to keep track of charge polarity, all discussions of electric charge movement will be described from the perspective of positive charges. Do not be frustrated if you look in either a basic physics or fundamental electronics book and find out that the polarity of in individual electron is negative.
Virtually all electronic product application manuals and most electronic instruments indicate either a concentration of positive charge (voltage) or the flow of positive charge (current). This no doubt stems from the historical representations of these phenomena by mathematicians. If given the opportunity, the positive electrical charge will begin to move in a direction from a higher voltage to a lower voltage.
This is just like a ball, or a whole bunch of marbles, rolling down a hill. They will roll from a high point to a low point under the influence of gravity. They will only stop when the ground changes shape to block their motion. This concept is very important to the operation of all electrical appliances, including every piece of high technology equipment mentioned earlier. This fact is also very important when considering how to charge a battery. What controls the movement of the charge along a path suitable to conduct electricity is two things. First, how much electrical potential is there to force the charge to move and second, how much resistance does the path offer to the movement of electric charge.
The resistance of the path is like the shape of the ground. By cleverly constructing the conductive path for electron movement and altering the resistance of that path at strategic locations, a wide variety of interesting electron motions can be produced, resulting in a great number of useful work functions. The fundamental unit of resistance to electric charge movement is the OHM, named for George Simon Ohm, a German physicist (1787 to 1854).
Once the electric charge begins to move, an electric current results. This is probably the most familiar form of electricity to everyone who uses electrical power. Truthfully, it is only when electric charge is in motion that we can extract any useful work or information from the machines that control both the paths through which the electric charge moves and the size of the electric current. The size (or amplitude) of the electric current is described by the quantity of electric charge that moves past a reference point along a reference conductive path during a fixed reference time period.
The fundamental unit of electrical current is the AMPERE, named for Andre Marie Ampere, a French physicist (1775 to 1836). To give you some perspective on the size of an Ampere (or Amp for short), 1 Amp = 1 Coulomb of electric charge moving every second.
In more concise mathematical terms, 1 Amp = 1 Coulomb / Second. There are a lot of electrons that make up 1 Amp of electric current (remember 100 million round trips to the moon). That also means that 6. 25 billion billion electrons must pass by the reference point every second. So now that we know the basic parts of electricity, what does this have to do with batteries and battery chargers First we should talk about how the Volts, Amps, and Ohms are related.
Remember, Volts result from charge (Coulombs) sitting still and Amps result from charge moving. So by talking about Volts and Amps, we`ve covered charge also. Another thing that George S. Ohm figured out is that the sizes or amplitudes of Volts, Amps, and Ohms are related. There is something called an electric circuit which is also very important when figuring out how to control Volts, Amps, an Ohms. An electric circuit is a collection of conductive paths that could possibly allow electric charge to move.
A CLOSED electric circuit will allow charge to move; an OPEN electric circuit will not. But having a closed path to move through is not enough. There has to be something to push or pull the electric charge through the closed path. That something is voltage (electric potential), in sufficient quantity and with the correct polarity to cause the charge not only to move, but also to move in the correction direction. Here is where Mr. Ohm made himself famous, or at least it is what he is most remembered for. Ohm`s Law defines how the electric charge moves by a very simple relationship. The size of an electric current is directly proportional to the size of the voltage pushing it and inversely proportional to the size of the resistance trying to stop it or slow it down, in the same closed electric circuit.
Mathematically, if we use the letter I to represent current (Amps) and V to represent voltage (Volts) and R to represent resistance (Ohms), then the equation looks like this: I = (V/R). This is the fundamental form of Ohm`s Law. Another German physicist Gustav Robert Kirchoff (1824 to 1887) established the laws governing the voltage and current distribution in complex circuit arrangements.
Most electric circuit analysis textbooks refer to Kirchoff`s laws with about the same regularity as Ohm`s law. Without belaboring the point too much, please don`t be to mystified by the use of the letter I to represent electric current.
In some texts you will see the letter E used to represent voltage. In that case the reasoning is because voltage is equal to Electric potential. Often times the particular symbol used simply result from a limited English alphabet used to represent more than 26 variables. Also, there are foreign language or proper name considerations. The R used for resistance could have just as easily been an O , in honor of Mr. Ohm, or an A could have been used for electric current in honor of Mr. Ampere. You get the picture. To try to get a better understanding of electrical potential and charge motion, consider the analogy between electrical potential and gravitational potential as illustrated by Figures 1 & 2.
The direct analogy between distance and voltage potential breaks down in any context other than stored charge separated by conductive plates. In the most general sense, the voltage potential due to the accumulation of electric charge is directly proportional to the amount of charge and inversely proportional to the distance from the charge when making the voltage measurement.
But for the purposes of this discussion, the parallel plate capacitor analogy is adequate. Notice the comparison between Figures 1 & 2. The mechanical gate and the electrical switch are physically represented in the same manner. And yet, the context of the words OPEN and CLOSED are identically reversed. The mechanical system context is the one with which we are most familiar. The electrical circuit context is opposite in the sense that closed means to complete a conductive path for charge movement (current flow) and open means that the conductive path has been interrupted. Now let`s take the next step and see what happens when things start to move. In Figure 3, it is clear that the amount of objects flowing past the reference point during a fixed period of time is determined by both the quantity of objects at rest prior to the mechanical gate opening and by the speed at which they move past the reference point.
The slope of the path connecting the original rest position plane and the mechanical ground plane determines the speed. An interesting fact is that the time it will take an object to reach the ground will be identical whether it travels in a straight, vertical line or along a sloped line.
However, the sloped path is physically longer than the straight, vertical line, so that the speed along the sloped is greater than the speed along the straight, vertical line. Remember that speed = distance divided by time. So if the time is the same and the distance is larger, then the speed is larger. All of the relationships dealing with speed and motion in the mechanical system assume that there is no friction.
We`ve taken a little literary license with the use of speed in Figure 4. As it turns out, the speed of charge movement is very fast, all the time. Actually in all but the most bizarre conductive path configurations, the speed of charge movement is at or very near the speed of light, a mere 186, 000 or so miles per second. So on a typical electric circuit board, measuring less than 1 foot in any direction, all parts of the circuit will be energized in a small (very, very small) fraction of a second.
Truthfully, it is difficult to come up with a complete, simple analogy to illustrate the behavior of electric charge in motion. Another popular analogy is that of fluid motion. The intuitive comparison between water pressure and voltage is appealing. But when it comes to describing the cause and effect relationships that determine the amplitude of electric current, that analogy breaks down too.
Continuing with the sloped path mechanical analogy, in Figure 3, it is more correct to say that the speed of the marbles is inversely proportional to the slope of the path. The more gradual slope represents a longer distance, and therefore a larger speed. In Figure 4, the true speed of the charge nearly constant everywhere, but for the sake of argument, let`s try to relate the slope of the path to the RESISTANCE to charge motion along the path.
Again, beginning with the slope of the mechanical path in Figure 3, the smaller, or more gradual the slope between the initial rest plane and the ground plane, the greater the speed, and therefore the larger the mechanical current. In electrical terms, considering Ohm`s Law, a larger current results from a smaller resistance. So the mechanical slope is directly proportional to the electrical resistance. You really don`t want to think about this too much, because there are many conditions where the analogy breaks down, but hopefully it gives you some perspective on how to relate electrical charge and its motion to something more familiar.
The last symbol on the right is also used for a battery. The long and short horizontal lines are used to indicate individual cells. So technically, 6 pairs of large and small horizontal lines would represent a 12 Volt battery. But practically, only 2 pairs of horizontal lines are usual by just dividing two numbers: 🔗 External reference
A collection of stationary electric charges signifies stored or potential electrical energy, which can be quantified by voltage. The unit of electrical potential is the volt, named after Italian physicist Alessandro Volta. Discussions of electric charge movement are typically framed from the perspective of positive charges. It is essential to note that while individual electrons possess a negative charge, most electronic manuals and instruments indicate positive charge concentrations or flows. Electric charges move from higher to lower voltage, akin to marbles rolling down a hill. The movement of charge is governed by the electrical potential and the resistance of the conductive path. The unit of resistance is the ohm, named after German physicist George Simon Ohm. When electric charge moves, it generates an electric current, which is the most familiar form of electricity. The size of the electric current, measured in amperes, corresponds to the quantity of charge passing a reference point over time.
The relationship between volts, amps, and ohms is vital for understanding electricity. An electric circuit, which comprises conductive paths, allows charge movement when closed, while an open circuit does not. Voltage, essential for driving charge through a circuit, must be sufficient and correctly polarized. Ohm's Law defines the relationship between current, voltage, and resistance, expressed mathematically as I = V/R. Kirchoff's laws further govern voltage and current distribution in complex circuits.
To understand electrical potential and charge motion, analogies to gravitational potential and fluid motion can be useful, though they have limitations. The speed of charge movement is nearly constant, approaching the speed of light. In typical circuits, all components become energized almost instantaneously. The analogy of fluid motion can be employed to compare water pressure with voltage, although it can be misleading in certain contexts.
In terms of circuit representation, batteries are depicted with long and short horizontal lines indicating individual cells, with pairs of lines representing the voltage of the battery.
In summary, the study of electricity encompasses the exploration of charge behavior and its implications for technology, governed by fundamental principles such as Ohm's Law and Kirchoff's laws. Understanding these concepts is crucial for the design and analysis of electrical circuits and systems.The study of electricity revolves around a few common terms that describe the behavior of electrical charge. Electrical charge and its associated phenomena are a fundamental part of the world that we live in. The understanding and use of electricity is largely responsible for the advanced technology that we enjoy today: electric light, heat, digit
al computers, television, music on CD, DVD video, radar, microwave ovens, cell phones, and on and on and on. The first recorded studies of natural attractive phenomena occurred among the ancient Greeks over 2, 500 years ago.
That`s right, over 2 thousand 5 hundred years ago. Over the last 2 or 3 hundred years, and particularly in the last century, that understanding has grown tremendously. In fact, some of the most interesting work relative to this limited discussion was done over a 40-year span between 1785 and 1826.
The fundamental unit of electric charge is the COULOMB, named for Charles Augustin de Coulomb, a French physicist (1736-1806). The smallest concentration of charge is contained in a single electron, a subatomic particle. The Coulomb is an extremely large amount of charge, or stated more precisely, an electric charge equal to 1 Coulomb requires an extremely large number of electrons.
The charge of a single electron is 0. 00000000000000000016 Coulombs. That`s 18 zeros in front of the 16. Stated in the notation that scientists prefer, called coincidentally, scientific notation, that amount of charge would be 1. 6 x 10-19 Coulombs. So 1 Coulomb of electric charge represents 6. 25 x 1018 electrons or 6, 250, 000, 000, 000, 000, 000 electrons. That`s a whole bunch of electrons (6. 25 billion billion or if you prefer 6. 25 million trillion). In fact, if each electron was a large as a marble, with a ½ inch diameter, you could line them up end to end in a straight line and reach from the earth to the moon and back over 100 million times.
So what do we know about electric charge except that the charge on a single electron is pretty small A collection of electric charges standing still represents an amount of stored, or potential electrical energy. A more convenient way to look at the stored electrical energy within a collection of electric charges standing still is the potential ability for the electric charges to move.
In this context we speak about an electrical potential , described numerically or quantified by an amount of voltage. The fundamental unit of electrical potential is the VOLT, named for Alessandro Volta, an Italian physicist (1745-1827).
To avoid the inevitable confusion resulting from trying to keep track of charge polarity, all discussions of electric charge movement will be described from the perspective of positive charges. Do not be frustrated if you look in either a basic physics or fundamental electronics book and find out that the polarity of in individual electron is negative.
Virtually all electronic product application manuals and most electronic instruments indicate either a concentration of positive charge (voltage) or the flow of positive charge (current). This no doubt stems from the historical representations of these phenomena by mathematicians. If given the opportunity, the positive electrical charge will begin to move in a direction from a higher voltage to a lower voltage.
This is just like a ball, or a whole bunch of marbles, rolling down a hill. They will roll from a high point to a low point under the influence of gravity. They will only stop when the ground changes shape to block their motion. This concept is very important to the operation of all electrical appliances, including every piece of high technology equipment mentioned earlier. This fact is also very important when considering how to charge a battery. What controls the movement of the charge along a path suitable to conduct electricity is two things. First, how much electrical potential is there to force the charge to move and second, how much resistance does the path offer to the movement of electric charge.
The resistance of the path is like the shape of the ground. By cleverly constructing the conductive path for electron movement and altering the resistance of that path at strategic locations, a wide variety of interesting electron motions can be produced, resulting in a great number of useful work functions. The fundamental unit of resistance to electric charge movement is the OHM, named for George Simon Ohm, a German physicist (1787 to 1854).
Once the electric charge begins to move, an electric current results. This is probably the most familiar form of electricity to everyone who uses electrical power. Truthfully, it is only when electric charge is in motion that we can extract any useful work or information from the machines that control both the paths through which the electric charge moves and the size of the electric current. The size (or amplitude) of the electric current is described by the quantity of electric charge that moves past a reference point along a reference conductive path during a fixed reference time period.
The fundamental unit of electrical current is the AMPERE, named for Andre Marie Ampere, a French physicist (1775 to 1836). To give you some perspective on the size of an Ampere (or Amp for short), 1 Amp = 1 Coulomb of electric charge moving every second.
In more concise mathematical terms, 1 Amp = 1 Coulomb / Second. There are a lot of electrons that make up 1 Amp of electric current (remember 100 million round trips to the moon). That also means that 6. 25 billion billion electrons must pass by the reference point every second. So now that we know the basic parts of electricity, what does this have to do with batteries and battery chargers First we should talk about how the Volts, Amps, and Ohms are related.
Remember, Volts result from charge (Coulombs) sitting still and Amps result from charge moving. So by talking about Volts and Amps, we`ve covered charge also. Another thing that George S. Ohm figured out is that the sizes or amplitudes of Volts, Amps, and Ohms are related. There is something called an electric circuit which is also very important when figuring out how to control Volts, Amps, an Ohms. An electric circuit is a collection of conductive paths that could possibly allow electric charge to move.
A CLOSED electric circuit will allow charge to move; an OPEN electric circuit will not. But having a closed path to move through is not enough. There has to be something to push or pull the electric charge through the closed path. That something is voltage (electric potential), in sufficient quantity and with the correct polarity to cause the charge not only to move, but also to move in the correction direction. Here is where Mr. Ohm made himself famous, or at least it is what he is most remembered for. Ohm`s Law defines how the electric charge moves by a very simple relationship. The size of an electric current is directly proportional to the size of the voltage pushing it and inversely proportional to the size of the resistance trying to stop it or slow it down, in the same closed electric circuit.
Mathematically, if we use the letter I to represent current (Amps) and V to represent voltage (Volts) and R to represent resistance (Ohms), then the equation looks like this: I = (V/R). This is the fundamental form of Ohm`s Law. Another German physicist Gustav Robert Kirchoff (1824 to 1887) established the laws governing the voltage and current distribution in complex circuit arrangements.
Most electric circuit analysis textbooks refer to Kirchoff`s laws with about the same regularity as Ohm`s law. Without belaboring the point too much, please don`t be to mystified by the use of the letter I to represent electric current.
In some texts you will see the letter E used to represent voltage. In that case the reasoning is because voltage is equal to Electric potential. Often times the particular symbol used simply result from a limited English alphabet used to represent more than 26 variables. Also, there are foreign language or proper name considerations. The R used for resistance could have just as easily been an O , in honor of Mr. Ohm, or an A could have been used for electric current in honor of Mr. Ampere. You get the picture. To try to get a better understanding of electrical potential and charge motion, consider the analogy between electrical potential and gravitational potential as illustrated by Figures 1 & 2.
The direct analogy between distance and voltage potential breaks down in any context other than stored charge separated by conductive plates. In the most general sense, the voltage potential due to the accumulation of electric charge is directly proportional to the amount of charge and inversely proportional to the distance from the charge when making the voltage measurement.
But for the purposes of this discussion, the parallel plate capacitor analogy is adequate. Notice the comparison between Figures 1 & 2. The mechanical gate and the electrical switch are physically represented in the same manner. And yet, the context of the words OPEN and CLOSED are identically reversed. The mechanical system context is the one with which we are most familiar. The electrical circuit context is opposite in the sense that closed means to complete a conductive path for charge movement (current flow) and open means that the conductive path has been interrupted. Now let`s take the next step and see what happens when things start to move. In Figure 3, it is clear that the amount of objects flowing past the reference point during a fixed period of time is determined by both the quantity of objects at rest prior to the mechanical gate opening and by the speed at which they move past the reference point.
The slope of the path connecting the original rest position plane and the mechanical ground plane determines the speed. An interesting fact is that the time it will take an object to reach the ground will be identical whether it travels in a straight, vertical line or along a sloped line.
However, the sloped path is physically longer than the straight, vertical line, so that the speed along the sloped is greater than the speed along the straight, vertical line. Remember that speed = distance divided by time. So if the time is the same and the distance is larger, then the speed is larger. All of the relationships dealing with speed and motion in the mechanical system assume that there is no friction.
We`ve taken a little literary license with the use of speed in Figure 4. As it turns out, the speed of charge movement is very fast, all the time. Actually in all but the most bizarre conductive path configurations, the speed of charge movement is at or very near the speed of light, a mere 186, 000 or so miles per second. So on a typical electric circuit board, measuring less than 1 foot in any direction, all parts of the circuit will be energized in a small (very, very small) fraction of a second.
Truthfully, it is difficult to come up with a complete, simple analogy to illustrate the behavior of electric charge in motion. Another popular analogy is that of fluid motion. The intuitive comparison between water pressure and voltage is appealing. But when it comes to describing the cause and effect relationships that determine the amplitude of electric current, that analogy breaks down too.
Continuing with the sloped path mechanical analogy, in Figure 3, it is more correct to say that the speed of the marbles is inversely proportional to the slope of the path. The more gradual slope represents a longer distance, and therefore a larger speed. In Figure 4, the true speed of the charge nearly constant everywhere, but for the sake of argument, let`s try to relate the slope of the path to the RESISTANCE to charge motion along the path.
Again, beginning with the slope of the mechanical path in Figure 3, the smaller, or more gradual the slope between the initial rest plane and the ground plane, the greater the speed, and therefore the larger the mechanical current. In electrical terms, considering Ohm`s Law, a larger current results from a smaller resistance. So the mechanical slope is directly proportional to the electrical resistance. You really don`t want to think about this too much, because there are many conditions where the analogy breaks down, but hopefully it gives you some perspective on how to relate electrical charge and its motion to something more familiar.
The last symbol on the right is also used for a battery. The long and short horizontal lines are used to indicate individual cells. So technically, 6 pairs of large and small horizontal lines would represent a 12 Volt battery. But practically, only 2 pairs of horizontal lines are usual by just dividing two numbers: 🔗 External reference
Related Circuits
Observing the bottom of a valve reveals the wires connected to each electrode and the valve base pins. Therefore, specific valve data or pin-outs will not be provided, as this information is widely accessible from various sources, and most...
Fluorescent lamps, despite their long presence, remain enigmatic to many individuals due to their complex operational mechanisms. The lamp consists of a gas mixture, primarily containing mercury, which, when energized as an arc, produces a significant amount of short-wave...
This is a programmable frequency multiplier that typically utilizes digital logic integrated circuits. The synthesizer is designed to multiply a reference frequency by a programmable factor to achieve virtually any desired frequency. For instance, with a reference frequency of...
Capacitive proximity sensing has gained significant interest among audiences over the past year. At the end of this article, a list of related articles published at Planet Analog is provided for further reading. A simple proximity sensor is designed...
The ladder logic programming method is a widely utilized approach in the programming of electrical simulation schematic control systems. This method primarily serves to make decisions regarding whether specific load circuits should be opened or closed. To comprehend ladder...
FM receivers are primarily of the superheterodyne type. To understand FM radio receivers, it is essential to consider the key differences between AM and FM signals. While it may seem obvious, these differences are significant. An AM receiver depends...