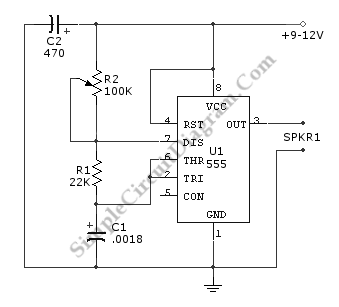
a better sine wave

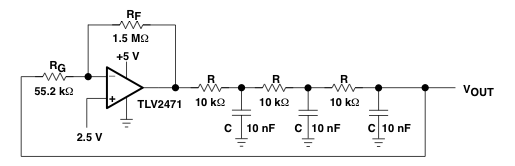
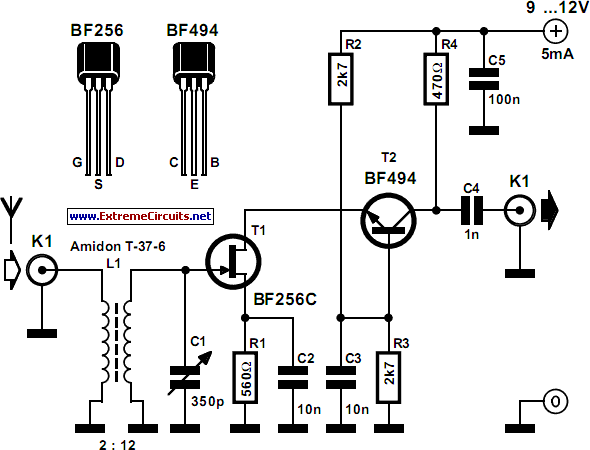
The operational amplifier (op-amp) is configured for 50x amplification, functioning similarly to a comparator. With this setup, a 50 mV deviation from the 2.5V reference will push the output to its limits. The output signal resembles a heavily clipped sine wave due to the presence of three resistors and three capacitors, which create three RC low-pass filters in series. These filters eliminate higher frequencies, resulting in a cleaner sine wave output. The frequency is influenced by phase shifts, with each RC filter introducing a 60° phase shift at a specific frequency. Consequently, three filters in series will produce a total phase shift of 180°. The feedback to the inverting pin of the op-amp generates an output that is 180° out of phase with the input signal. Selecting appropriate resistor (R) and capacitor (C) values is essential for achieving the desired frequency, and it is recommended to use identical values for consistency. In this case, 0.1 µF capacitors were utilized, which are ten times larger than the original 10 nF capacitors. This configuration results in oscillation at approximately 440 Hz, corresponding to a pure musical A tone. To induce oscillation, an increased gain was necessary, with resistor values of RF set to 1 MΩ and RG to 22 kΩ, yielding a gain of 47. The RG value may be slightly low, which could load the last RC section. This circuit exemplifies a negative feedback loop, stabilizing oscillation due to a delay of about 2.27 ms through the RC chain. The op-amp oscillates around its midpoint (2.5V at the non-inverting input) in a controlled manner. The amplitude is capped by clipping at the op-amp's limits, while the gain sufficiently maintains the signal swing. Upon power-up, a clean signal is observed, with the second harmonic being approximately 42 dB below the fundamental frequency, resulting in about 0.8% harmonic distortion. This sine wave circuit can be further enhanced with an additional op-amp stage to achieve the desired output level, especially if significant current is required.

The operational amplifier circuit described operates effectively as an oscillator, utilizing a combination of RC low-pass filters to shape the output waveform. The configuration allows for a significant amplification factor, which is critical in achieving the desired output characteristics. The inclusion of three RC filters not only serves to filter out unwanted high-frequency components but also plays a pivotal role in phase manipulation, which is essential for sustaining oscillation. Each RC stage introduces a phase shift that is cumulative, ensuring that the feedback mechanism aligns correctly to maintain stable oscillation.

The choice of capacitors and resistors is crucial; using larger capacitors such as 0.1 µF allows for lower frequency oscillation, which is suitable for audio applications. The resistor values are also carefully selected to maintain the necessary gain while ensuring that the circuit remains stable and does not introduce excessive loading on the output. The gain adjustment via RF and RG is a common practice in op-amp circuits, allowing for fine-tuning of the output characteristics based on the specific application requirements.

The negative feedback mechanism employed in this circuit is a foundational principle in analog electronics, promoting stability and precision in the output signal. By delaying the feedback through the RC network, the circuit can effectively control the oscillation, preventing runaway conditions that could lead to distortion or instability. The observed startup ramp and stabilization indicate a well-designed circuit that efficiently transitions to its steady-state operation.

Overall, this op-amp oscillator circuit exemplifies the practical application of feedback and filtering in generating a clean sine wave output, suitable for various electronic applications, including signal generation and audio processing. The ability to modify the output level with additional amplification stages further enhances its versatility, making it a valuable component in analog circuit design.This one is actually a bit simpler to explain: the op-amp is set up with 25. 50x amplification, i. e almost a comparator (with 50x amplification, a 50 mV input above or below the 2. 5V will drive the output to its limit). And indeed, the output signal of the op-amp looks somewhat like a heavily clipped sine wave: The 3 resistors and 3 capacitors crea te 3 RC low-pass  filters in series, removing all the higher frequencies, i. e. harmonics. A fairly clean sine wave comes out at the end, as you can see here: The frequency is determined by phase shifts . Each RC filter changes the phase of its input signal, and it will be by 60 ° at a certain frequency, so that 3 of them in series will then shift it by 180 °.

Since the signal is fed back to the -  pin of the op-amp, that`s exactly the proper signal to generate the opposite output, i. e. shifted 180 ° out of 360 °. This analog stuff gets complicated don`t worry too much about it: just pick R and C values to get the right frequency, and make all of them the same.

I used 0. 1 µF caps i. s. o. 10 nF caps, i. e. 10x larger than the original circuit. With these values, the oscillation in my setup turned out to occur at just about 440 Hz, i. e. a pure musical A  tone! I did have to increase the gain (1. 5 M © / 55. 2 k © = 27 in the above setup) to force oscillation. I changed RF to 1 M © and RG to 22 k ©, for a gain of 47. This RG value is a bit low, it loads down the last RC section quite a bit. What you`re seeing here is a classical example of a negative feedback loop, which ends up in a very stable state of oscillation. It oscillates because we`re delaying the feedback signal by about 2. 27 ms through the RC chain. So the op-amp constantly overshoots around its mid-point (the 2. 5V applied to the +  input), but does so in a very controlled way. The amplitude can`t increase any further, since the op-amp is clipping at its limits already, and the amplification factor is large enough to keep boosting the swing up to that limit.

You can see the startup ramp and stabilization when powering up: A clean signal compared to the previous experiment. The 2nd harmonic is ‰ 42 dB below the fundamental wave, the rest is even lower. Using this calculator, we can see that this represents about 0. 8% harmonic distortion. Glad you got a working sinewave circuit! It seems easy enough to use another opamp stage to get whatever level output you need, I assume you`ll be using a separate driver anyway if you need significant current.

🔗 External reference