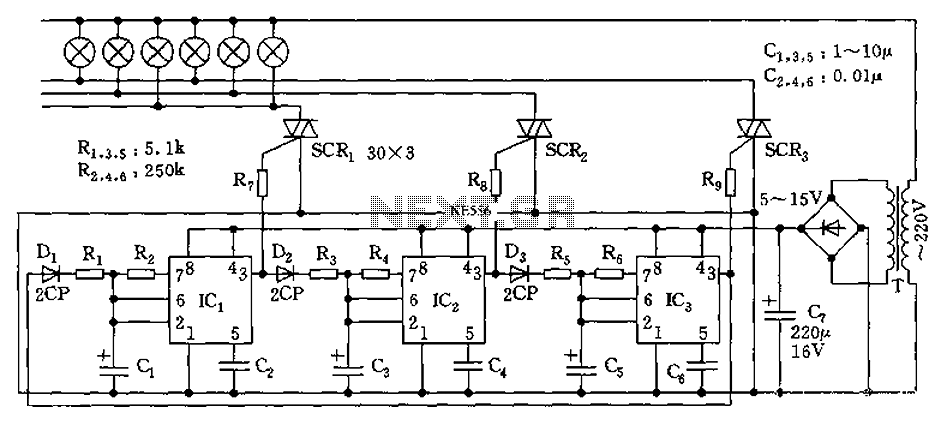
bassman tonestack low frequency

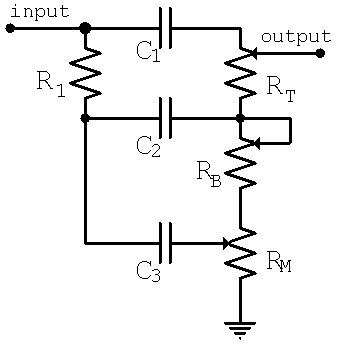
Bass and midrange frequencies are significantly influenced by Marshall's considerable adjustment of R1 and are somewhat affected by the 10-percent increase in C2 and C3. The following paragraphs will explain how the circuit responds to bass and midrange frequencies, calculating gain and transition frequencies for optimal bass and midrange settings. Once these essential characteristics are established, the impact of Marshall's modifications will be evident. The analysis will conclude with an overview of the low and midrange frequency effects resulting from Marshall's changes to the 5F6-A tone stack. A traditional approach to analyzing tone stacks involves the magnitude plots of Hendrik Wade Bode, which gained popularity in the 1950s and 1960s. This analysis will examine the 5F6-A tone stack and Marshall's modifications in the context of that era. The analysis begins by considering bass and midrange frequencies with the bass control set to minimum and the midrange control set to maximum. At these frequencies, C1 behaves as an open circuit. Due to the high input impedance of the long-tailed-pair phase inverter, there is minimal current flowing through the treble control, rendering its setting inconsequential. According to Ohm's Law, the voltage across the control remains essentially the same for midrange and bass frequencies. With the bass control at minimum and the midrange control at maximum, capacitors C2 and C3 are in parallel. The circuit can be described as follows: The frequency response as a function of s has a pole at p if the denominator equals zero when s = p. The response has a zero at z if the numerator equals zero when s = z. Poles and zeros are critical transition points in the frequency response. By deriving an equation for one of the poles as a function of two or three component values, the effect of these component values on the transition point can be understood. Analyzing the extremes of frequency, at DC (s = 0), H(s) = 0, resulting in zero output. At very high frequencies (s approaching infinity), the response becomes dominated by a, leading to a specific output behavior. These observations align with expectations, as at DC, C2+3 acts as an open circuit, yielding zero output, while at high frequencies, it behaves as a short circuit, forming a simple attenuator from the voltage divider of R1 and RM. Consequently, this configuration functions as a high-pass filter. Beyond a certain cutoff frequency, the gain remains relatively constant, while below this frequency, attenuation increases as frequency decreases. In decibels, audio attenuation with the midrange control set to maximum is observed. With R1 at 56k and RM at 25k, a gain of -10dB is achieved. The Marshall JMP50 Model 1987 reduces R1 to 33k, resulting in -7dB of gain. Thus, the output signal at midrange frequencies with the midrange control at maximum is 3dB higher in the Marshall configuration. Utilizing the 5F6-A component values, the cutoff frequency is calculated to be f-3dB = 49Hz. In the Marshall configuration, with C2+3 increased by 10 percent and R1+RM decreased by 28 percent, the cutoff frequency rises to f-3dB = 62Hz. For plotting purposes, the overall gain in dB can be decomposed into two components: one associated with the gain constant and the zero, and the other with the pole. For frequencies below 49Hz, a straight line at 0dB is plotted. At 49Hz, a line is extended that decreases at a rate of 20dB per decade. The approximate gain is the sum of the two components plotted. Below 49Hz, it is a straight line declining at a rate of 20dB per decade until it reaches -10dB at 49Hz. Above 49Hz, the gain remains constant at -10dB. The actual gain at the breakpoint is 3dB lower, as illustrated in the figure. At frequencies significantly higher or lower than 49Hz, the described behavior continues.

The circuit described pertains to a tone stack configuration used in guitar amplifiers, particularly the 5F6-A and its modified version by Marshall. The tone stack serves to shape the tonal characteristics of the audio signal by adjusting the bass and midrange frequencies. The component values, including resistors R1 and RM and capacitors C2 and C3, play a crucial role in determining the frequency response and gain of the circuit.

In practical terms, the adjustments made by Marshall to the component values are aimed at enhancing the amplifier's tonal response, particularly in the midrange frequencies, which are critical for achieving a rich and full sound. The reduction of R1 and the increase in capacitance values for C2 and C3 lead to a shift in the cutoff frequency, allowing for greater emphasis on the desired frequency ranges.

The analysis utilizes Bode plots to visualize the frequency response of the circuit, providing insight into how the different components interact to affect gain and attenuation across the audio spectrum. Understanding these dynamics is essential for engineers and technicians working with guitar amplifiers, as it enables them to optimize tonal characteristics based on player preferences and musical styles.

Overall, the modifications introduced by Marshall to the 5F6-A tone stack exemplify the ongoing evolution of amplifier design, where small changes in component values can lead to significant alterations in sound quality and performance. This understanding of frequency response and gain characteristics is vital for anyone involved in the design, modification, or repair of guitar amplifiers.Bass and midrange frequencies are greatly affected by Marshall`s substantial adjustment of R1 and somewhat influenced by the 10-percent increase in C2 and C3. In the paragraphs that follow we will describe how the circuit reacts to bass and middle-range frequencies, computing gain and transition frequencies for maximum bass and maximum midrange se

ttings. Once these key characteristics are known, the effects of Marshall`s modifications will be clearly evident. Finally we wrap up our analysis by drawing some overall conclusions on the low and midrange-frequency effects of Marshall`s modifications to the 5F6-A tone stack.

The classic way to analyze tone stacks is by using the magnitude plots of Hendrik Wade Bode, which were very popular in the 1950s and 1960s. So in the spirit of the time, I`m going analyze the 5F6-A tone stack and Marshall`s modifications in the way they were understood back then.

To begin our analysis, let`s look at bass and midrange frequencies when the bass control is at minimum and the midrange control is at maximum. At bass and middle-range frequencies C1 acts as an open circuit. Because of the high input impedance of the long-tailed-pair phase inverter, there is almost no current flowing through the treble control, thus making its particular setting irrelevant.

According to Ohm`s Law, the voltage at the top and bottom of the control is essentially the same at midrange and bass frequencies. With the bass control at minimum and the midrange control at maximum, the capacitors C2 and C3 are in parallel.

Putting all of this together, the circuit looks like this: The frequency response as a function of s has a pole at p if the denominator of the response equals zero when s = p. (If the variable "s" looks unfamiliar, please see our tutorial on Laplace notation. ) The response has a zero at z if the numerator equals zero when s = z. Poles and zeros represent key transition points in the frequency response. If we can derive an equation for one of the poles as a function of two or three component values, for example, then we know how these part values affect this particular transition point.

Let`s take a look at the extremes of frequency. At DC, where s = 0 we note that H(s) = 0 and there is zero output. At extremely high frequencies, where s approaches infinity, it becomes much larger than a and the response is Both of these conditions make sense, because at DC C2+3 is an open circuit, producing zero output, and at very high frequencies it acts as a short circuit, producing a simple attenuator formed by the voltage divider of R1 and RM. So we essentially have a simple high-pass filter. Above a certain cutoff frequency the gain is fairly constant. Below it there is increasing attenuation as the frequency decreases. In terms of dB, audio attenuation with the middle-range control set to maximum is With R1 = 56k and RM = 25k we get a gain of -10dB.

The Marshall JMP50 Model 1987 lowers the value of R1 to 33k, which provides -7dB of gain. We conclude that the output signal at middle-range frequencies, middle-range control at maximum, is 3dB higher in the Marshall. Using 5F6-A parts values we get f-3dB = 49Hz. In the Marshall, C2+3 is 10-percent higher but R1+RM is 28 percent lower, so the cutoff frequency rises to f-3dB = 62Hz.

To plot it we note that the overall gain in dB can be separated into the sum of two parts: one due to the gain constant and the zero and the other due to the pole: so for frequencies below 49Hz we plot a straight line at 0dB. At 49Hz we extend a line that decreases at a rate of 20dB per decade. The approximate gain is the sum of the two components that we have just plotted. Below 49Hz it is a straight line rising at the rate of 20dB per decade until it reaches -10dB at 49Hz.

Above 49Hz it remains a constant -10dB. The actual gain is 3dB lower at the break point, as shown in the figure. At frequencies much higher or much lower than 49H 🔗 External reference