Four-Output Filter Circuit

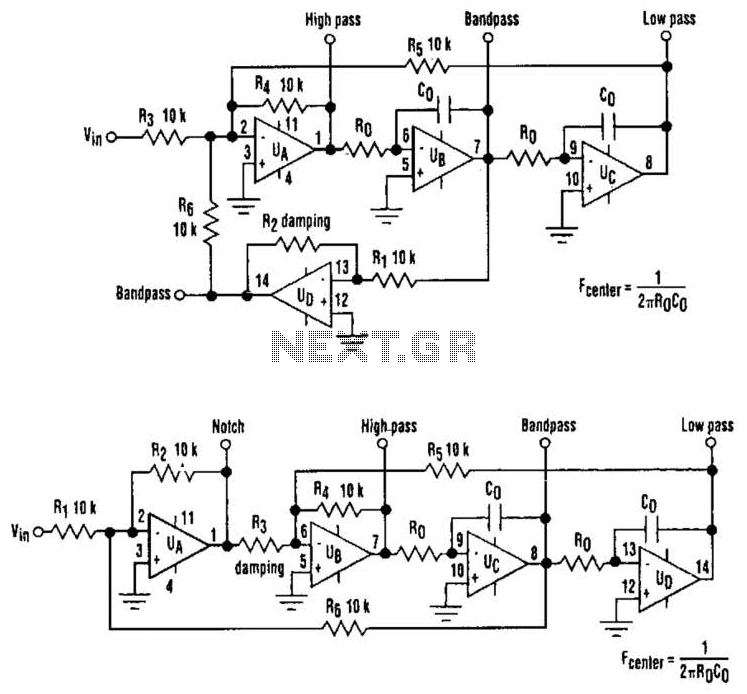
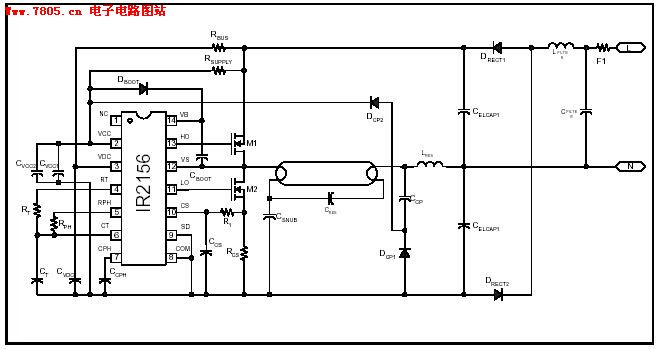
The classic state-variable (two-integrator) filter is well-known for its insensitivity to device parameter tolerances and its capability to provide three simultaneous separate outputs: high pass, bandpass, and low pass. These advantages often outweigh the requirement of a quad operational amplifier to implement the circuit. A modification of the classic design applies the input voltage via amplifier UD instead of UA, resulting in a bandpass output with a fixed peak gain that does not depend on the filter's Q factor. This configuration can yield a fourth notch-filter output if -R6 is utilized. If R, -R^ = R2, the gains of both the notch and bandpass outputs remain unity, irrespective of the Q factor, as determined by resistors R3, R1, R2, R4, R5, and R6. The resonant (or cutoff) frequency is defined by -1/R0 x CQ. Depending on the capacitor values and frequency, resistance R0 may also be incorporated into the same monolithic network for optimal space efficiency. Similar to the classic configuration, the resonant frequency can be electrically controlled by switching resistors R0 or by employing analog multipliers in series with the integrators.

The state-variable filter design employs a dual integrator configuration that enhances flexibility in signal processing applications. The three outputs—high pass, bandpass, and low pass—are achieved through the careful selection of feedback and feedforward components, enabling precise control over the filter characteristics. The modification that uses amplifier UD allows for a bandpass output that maintains a consistent peak gain, which is particularly beneficial in applications where gain stability is critical, such as audio processing or communication systems.

The notch filter output, achieved through the specific configuration of resistor R6, introduces additional utility by allowing unwanted frequency components to be attenuated without affecting the desired signal paths. This feature is advantageous in scenarios where noise suppression is necessary.

The relationship between the Q factor and the gains of the notch and bandpass outputs is crucial for achieving the desired filter response. The unity gain condition simplifies the design process, ensuring predictable behavior across various operational conditions. The resonant frequency, determined by the product of resistance R0 and capacitance CQ, can be adjusted dynamically, allowing for real-time tuning of the filter's response. The use of a monolithic network for resistance R0 not only conserves board space but also enhances reliability by minimizing the number of discrete components.

Incorporating analog multipliers in series with the integrators offers further versatility, enabling the implementation of complex filter responses and adaptive filtering techniques. This capability is particularly relevant in modern signal processing applications, where the ability to adjust filter parameters on-the-fly can significantly improve performance. Overall, the state-variable filter's architecture provides a robust solution for a wide range of electronic filtering needs, balancing performance, stability, and flexibility. The classic state-variable (two-integrator) filter (see Fig. A) is famous for its insensitivity to device parameter tolerances, as well as its ability to provide three simultaneous separate outputs: high pass, bandpass, and low pass. These advantages often offset the fact that a quad operational amplifier is needed to implement the circuit.

A modification of the classic scheme that applies the input voltage via amplifier UD, rather than UA provides a bandpass output with a fixed peak gain that doesn`t depend on the Q of the filter. It was found by using that configuration, a fourth notch-filter output can be obtained if - R6 (see Fig.

B). If R, -R^ = R2, the gains of both the notch and bandpass outputs are unity, regardless of the Q factor, as determined by R3, Rl, R2, R4, R5, and R6. The resonant (or cutoff) frequency is given by, - 1/R0 x CQ. Depending on the capacitor values and frequency, resistance R0 might also share the same monolithic network for maximum space economy.

As with the classic configuration, resonant frequency can be electrically controlled by switcliing resistors R0, or by using analog multipliers in series with the integrators. 🔗 External reference