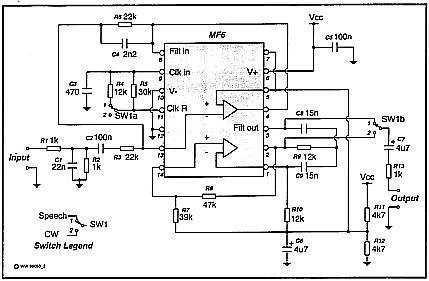
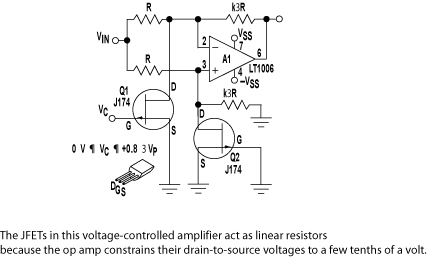
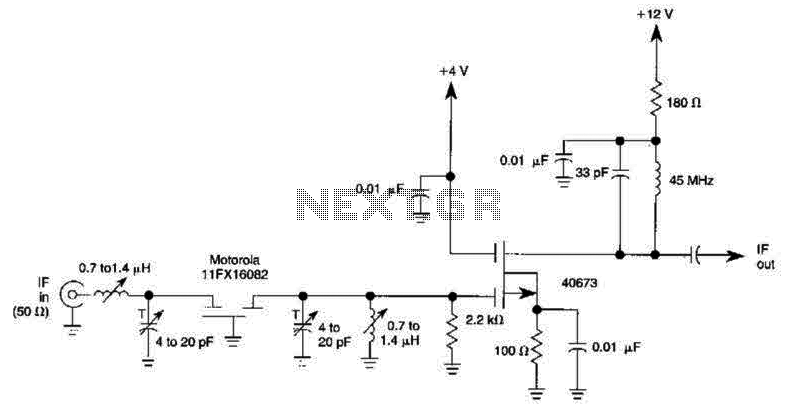
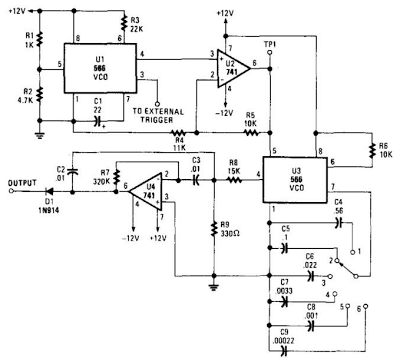
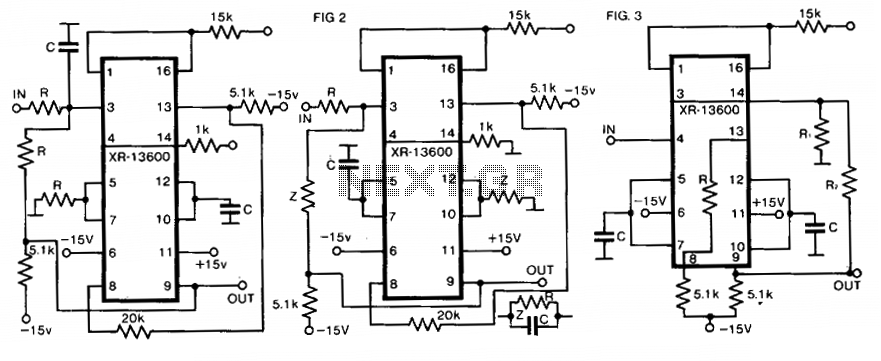
Multiple-feedback bandpass filter
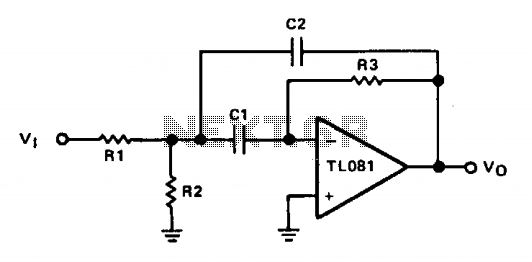
The operational amplifier (op amp) is configured in inverting mode. Resistor R3 connects the output to the inverting input, establishing the gain and the current through the frequency-determining capacitor, C1. Capacitor C2 provides feedback from the output to the junction of resistors R1 and R2. Capacitors C1 and C2 are always of equal value. Resistor R2 can be made adjustable to fine-tune the center frequency, which is calculated using the formula: f0 = 1 / (2π(R1 + R2)R3C). When designing a filter of this type, it is advisable to select values for C1 and C2 that are equal.
Typical audio filters utilize capacitor values ranging from 0.01 µF to 0.1 µF, which leads to reasonable values for the resistors.
The described circuit employs an operational amplifier in an inverting configuration, which is a common topology for implementing active filters. In this arrangement, the gain is primarily determined by the feedback resistor R3 and the input resistors R1 and R2. The relationship between these resistors directly influences the frequency response of the circuit.
The frequency-determining capacitor C1 plays a crucial role in setting the cutoff frequency of the filter. The feedback capacitor C2, which is equal in value to C1, ensures that the phase shift and frequency response remain consistent. This equality is vital for maintaining the desired filter characteristics.
The adjustable resistor R2 allows for fine-tuning of the center frequency, enabling the designer to optimize the filter for specific audio applications. The formula provided for the center frequency, f0, indicates that it is inversely proportional to the product of the resistors and the capacitance. Therefore, careful selection of R1, R2, and C1/C2 values is essential for achieving the desired filtering effect.
In practical applications, the capacitor values typically range from 0.01 µF to 0.1 µF. This range is standard for audio filters, as it provides a good balance between frequency response and component size. The chosen capacitor values will dictate the values of the resistors R1 and R2, ensuring that the filter operates effectively within the desired frequency range.
Overall, this op amp-based filter circuit provides a versatile solution for audio signal processing, with the ability to adjust the center frequency and maintain consistent performance through the careful selection of component values.The op amp is connected in the inverting mode. Resistor R3 from the output to the inverting input sets the gain and current through the frequency-determining capacitor, CI. Capacitor C2 provides feedback from the output to the junction of Rl and R2. CI and C2 are always equal in value. Resistor R2 may be made adjustable in order to adjust the center frequency which is determined from: 1 1 Rl + R2 a fo = 2TTC R3 R1 R2 When designing a filter of this type.it is best to select a value for CI and C2, keeping them equal.
Typical audio filters have capacitor values from 0.01 µf to 0.1 /µf which will result in reasonable values for the resistors. 🔗 External reference
Typical audio filters utilize capacitor values ranging from 0.01 µF to 0.1 µF, which leads to reasonable values for the resistors.
The described circuit employs an operational amplifier in an inverting configuration, which is a common topology for implementing active filters. In this arrangement, the gain is primarily determined by the feedback resistor R3 and the input resistors R1 and R2. The relationship between these resistors directly influences the frequency response of the circuit.
The frequency-determining capacitor C1 plays a crucial role in setting the cutoff frequency of the filter. The feedback capacitor C2, which is equal in value to C1, ensures that the phase shift and frequency response remain consistent. This equality is vital for maintaining the desired filter characteristics.
The adjustable resistor R2 allows for fine-tuning of the center frequency, enabling the designer to optimize the filter for specific audio applications. The formula provided for the center frequency, f0, indicates that it is inversely proportional to the product of the resistors and the capacitance. Therefore, careful selection of R1, R2, and C1/C2 values is essential for achieving the desired filtering effect.
In practical applications, the capacitor values typically range from 0.01 µF to 0.1 µF. This range is standard for audio filters, as it provides a good balance between frequency response and component size. The chosen capacitor values will dictate the values of the resistors R1 and R2, ensuring that the filter operates effectively within the desired frequency range.
Overall, this op amp-based filter circuit provides a versatile solution for audio signal processing, with the ability to adjust the center frequency and maintain consistent performance through the careful selection of component values.The op amp is connected in the inverting mode. Resistor R3 from the output to the inverting input sets the gain and current through the frequency-determining capacitor, CI. Capacitor C2 provides feedback from the output to the junction of Rl and R2. CI and C2 are always equal in value. Resistor R2 may be made adjustable in order to adjust the center frequency which is determined from: 1 1 Rl + R2 a fo = 2TTC R3 R1 R2 When designing a filter of this type.it is best to select a value for CI and C2, keeping them equal.
Typical audio filters have capacitor values from 0.01 µf to 0.1 /µf which will result in reasonable values for the resistors. 🔗 External reference