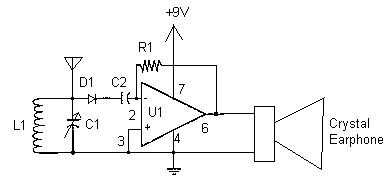
Op Amp based Hartley oscillator

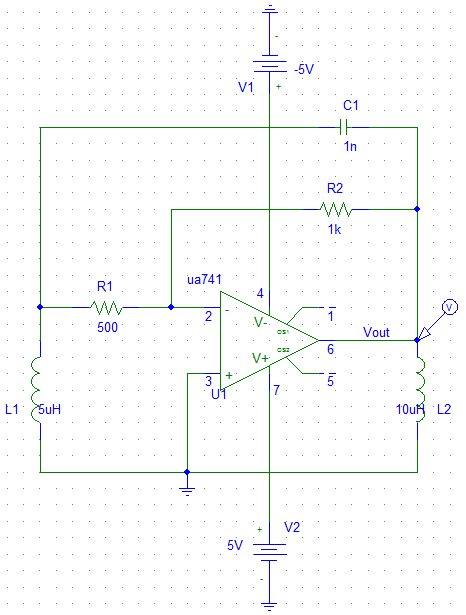
Construct an oscillator that meets several specifications. The primary requirement is to incorporate exactly one capacitor. Another requirement is to achieve a high quality factor (Q) and produce a sine wave output. The design under consideration is Hartley’s oscillator, which utilizes a single capacitor. There is a need to develop a biasing network and select an appropriate transistor to fulfill the oscillator's requirements. Additionally, it has been proposed to implement Hartley’s oscillator using an operational amplifier, as illustrated in the accompanying figure. A simulation has been conducted, indicating that the circuit should oscillate since the gain of the operational amplifier's negative feedback loop exceeds the ratio of L1 to L2. However, the oscillations begin and then diminish. The frequency of the decaying oscillations appears correct, but they do not persist. Attempts to increase the gain to excessive levels have not resolved the issue.

The Hartley oscillator is a type of LC oscillator that is known for its simplicity and effectiveness in generating sine wave outputs. In this design, the oscillator utilizes a single capacitor and two inductors (L1 and L2), which are critical in determining the oscillation frequency. The operational amplifier (Op-Amp) serves as the active element, providing the necessary gain to initiate and sustain oscillations.

In the proposed configuration, the Op-Amp is connected in a feedback loop that includes the single capacitor and the inductors. The feedback network is designed such that the phase shift around the loop is 360 degrees, which is essential for oscillation. The gain of the Op-Amp must be sufficiently high to compensate for any losses in the circuit and to satisfy the Barkhausen criterion for sustained oscillations. This criterion states that the product of the gain and the feedback factor must equal one at the frequency of oscillation.

The oscillation frequency can be calculated using the formula:

\[ f = \frac{1}{2\pi\sqrt{L1 \cdot L2 \cdot C}} \]

Where \( C \) is the capacitance of the single capacitor used in the design. The quality factor (Q) of the oscillator is determined by the ratio of the resonant frequency to the bandwidth of the oscillator. A high Q factor indicates a narrow bandwidth and sharper resonance, which is desirable for a clean sine wave output.

If the oscillations are observed to decay, it may indicate that the gain of the Op-Amp is not sufficient to maintain the oscillation. This could be due to several factors, including the selection of components, the configuration of the feedback network, or the characteristics of the Op-Amp itself. It is crucial to ensure that the Op-Amp used has low noise and sufficient bandwidth to support the desired frequency of oscillation.

In conclusion, the successful implementation of a Hartley oscillator using an operational amplifier hinges on careful selection of components, precise tuning of the feedback network, and ensuring that the operational amplifier provides adequate gain to sustain oscillations. Further analysis of the circuit parameters and component values may be necessary to achieve stable and continuous oscillation.Build an oscillator that will satisfy a few requirements. The main requirement is to have exactly one capacitor. Another one is to have high Q and sine wave output. I am considering Hartley`s oscillator design. Since it has only one cap. I don`t what to built the biasing network and select a transistor that will suit the oscillator`s needs, so I figured that there must be a way to build Hartley`s oscillator around an operational amplifier as shown on the figure below. I have made the simulation as shown above, and I believe it should oscillate, since the gain of the Op Amp negative feedback loop is greater than $frac{L1}{L2}$ ratio.

But the oscillations start and die. I can see that the frequency of the decaying oscillations is correct, but they would not sustain. I event tried to crack the gain up to some unreasonable number, but this doesn`t help at all. 🔗 External reference