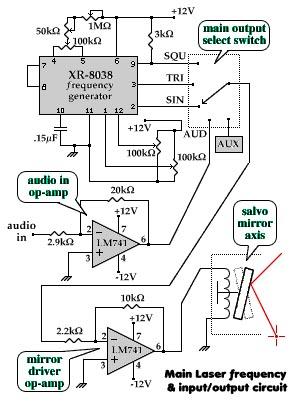
The same capacitance parameters easy to change the cutoff frequency of the low pass filter 24dB-oct

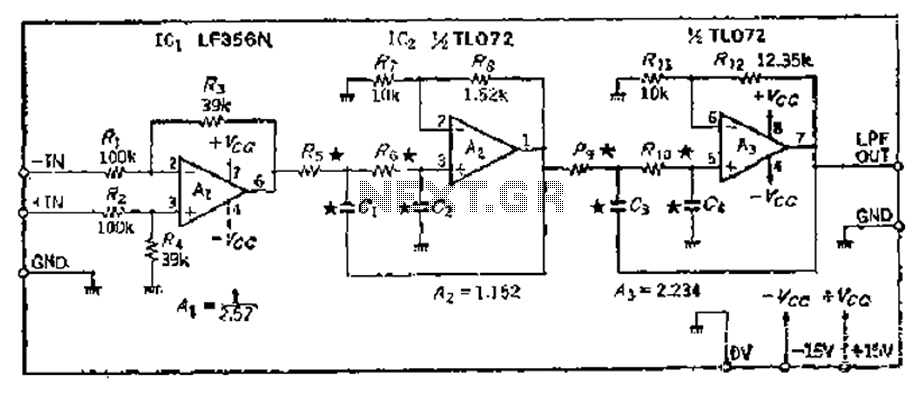
A 24 dB/octave Butterworth filter with a maximally flat characteristic is constructed using two filters, each capable of providing a 12 dB/octave response. This configuration allows for a 3 dB point adjustment. To achieve the desired cutoff frequency, adjustments are made to the gain, which is normalized to two units in the soil. The necessary adjustments are made using specific values: the first and second stages require adjustments of 0.541 and 1.306, respectively, to enhance the output gain according to the specified formula. The resistance path to ground is connected via a Phoenix connector, and the cutoff frequency is determined based on the provided calculations for feedback resistors. The library values for resistors are R1 at 2 kΩ and R2 at 12.35 kΩ. Since the filter has a passband gain, the input stage requires an attenuation of 1/2.53.

A 24 dB/octave Butterworth filter is a well-known design in analog signal processing, characterized by its maximally flat frequency response in the passband. This particular design employs two cascaded filters, each contributing a 12 dB/octave slope, resulting in a total of 24 dB/octave. The filters are designed to ensure a smooth transition between the passband and the stopband, minimizing ripple and phase distortion.

The 3 dB cutoff frequency is a critical parameter in filter design, marking the frequency at which the output power drops to half of its maximum value. In this case, the cutoff frequency can be fine-tuned through the adjustments made to the gain settings, which are normalized to two units in the soil context. The adjustments of 0.541 and 1.306 for the first and second stages, respectively, are essential for optimizing the filter's performance and achieving the desired frequency response.

The feedback mechanism in the circuit is vital for stabilizing the filter's response. The feedback resistors are calculated based on the specified parameters, with R1 set at 2 kΩ and R2 at 12.35 kΩ. These resistors help define the gain of the filter, ensuring that the output signal remains within the desired amplitude range while maintaining the filter's characteristic response.

Additionally, the connection to ground through a Phoenix connector ensures reliable performance and easy integration into larger systems. The calculated feedback path, as indicated, plays a crucial role in determining the overall behavior of the filter, particularly in managing the gain and stability of the output signal.

Overall, this filter design is suitable for applications requiring precise frequency selection and signal integrity, making it a valuable component in various electronic systems, including audio processing, communications, and instrumentation. The careful selection of component values and the attention to gain adjustments contribute to the robustness and effectiveness of the filter in practical applications.24dB/oc seven times Butterworth (maximally flat characteristic) constituted by the two filters, each box has two books enough filter (12dB/oct), in order to make a 3dB point tw o units into soil cutoff frequency normalized, must first and second mouth enough baskets at sub-cut adjustment thistle 0.541 and 1.306 fold to take the gain to improve port by value according to A. 3 a (l/mouth.) (Taboo for the series 1, 2) calculate the required gain.. Jic resistance path to ground is fed Phoenix iok0 time, cut off the feet according to B. (A.-1) x IO 10I calculate the feedback resistor hall., Library lI, R. 1. S2k mouth, R1. 12.35 ka Since the filter with passband gain, so the input stage 4. Attenuation of 1/2. 53.