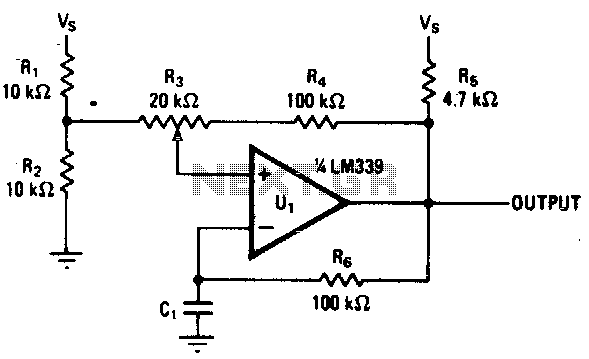
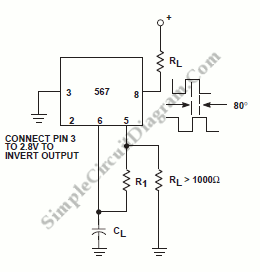
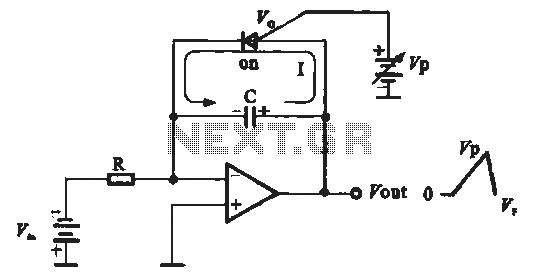
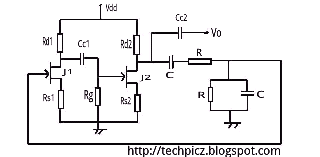
Colpitts Crystal Oscillator

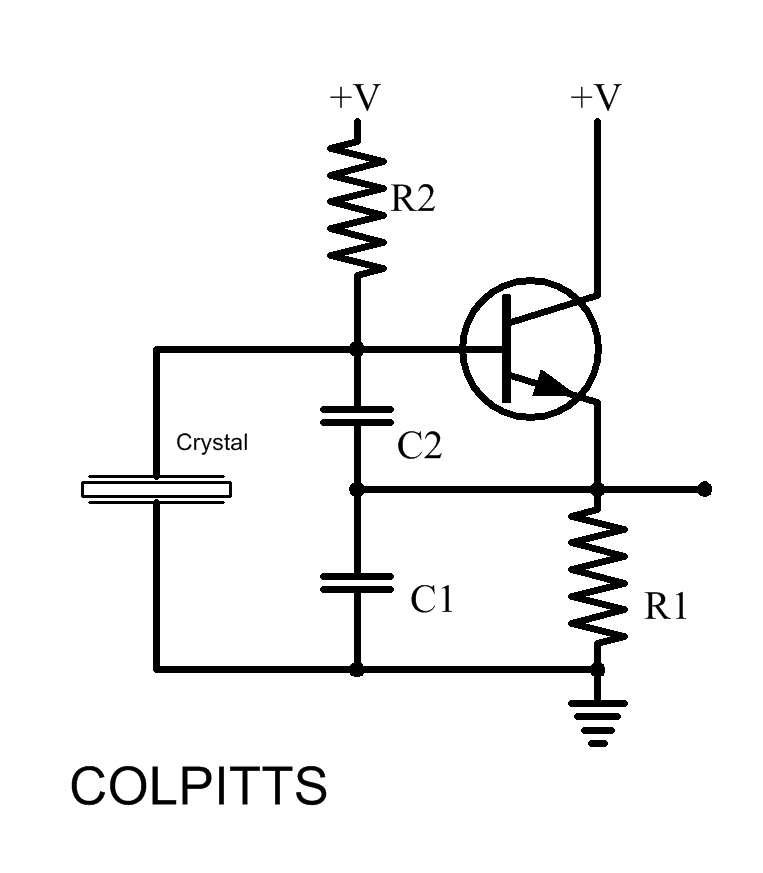
Inquiries about selecting the L, C, and R values to achieve a desired frequency are common. It is essential to understand the relationship between these components and the frequency they produce. The desired frequency can be calculated using the formula f = 1 / (2π√(LC)) for a resonant circuit, where f is the frequency in hertz, L is the inductance in henries, and C is the capacitance in farads. The resistance (R) can also affect the quality factor and bandwidth of the circuit, but it does not directly influence the resonant frequency.

To design a resonant circuit that achieves a specific frequency, the following steps can be employed:

1. **Determine the Desired Frequency**: Clearly define the target frequency (f) in hertz. This will serve as the basis for selecting the L and C values.

2. **Calculate Inductance and Capacitance**: Rearranging the resonant frequency formula allows for the calculation of either L or C when the other component is known. For example, if a specific inductance value is chosen, the corresponding capacitance can be calculated using C = 1 / (4π²f²L).

3. **Select Component Values**: Choose standard values for L and C that are readily available in the market. It is advisable to consider the tolerance and ratings of the components based on the application's requirements.

4. **Incorporate Resistance**: While resistance does not affect the resonant frequency directly, it is important to include it in the design to manage the circuit's bandwidth and quality factor (Q). The Q factor can be calculated using Q = f / Δf, where Δf is the bandwidth. Select R values that will provide the desired Q for the application.

5. **Simulation and Testing**: Before finalizing the design, it is prudent to simulate the circuit using software tools to verify the frequency response and make adjustments as necessary. Prototyping the circuit will also help in confirming the theoretical calculations.

By following these guidelines, a suitable combination of L, C, and R can be determined to achieve the desired frequency in a resonant circuit while ensuring optimal performance.Hey, Just wondering how to choose my L,C,R variables to achieve a desired frequency. Do I just choose any combination that yields X Mhz = 1 / ( 2pi *.. 🔗 External reference