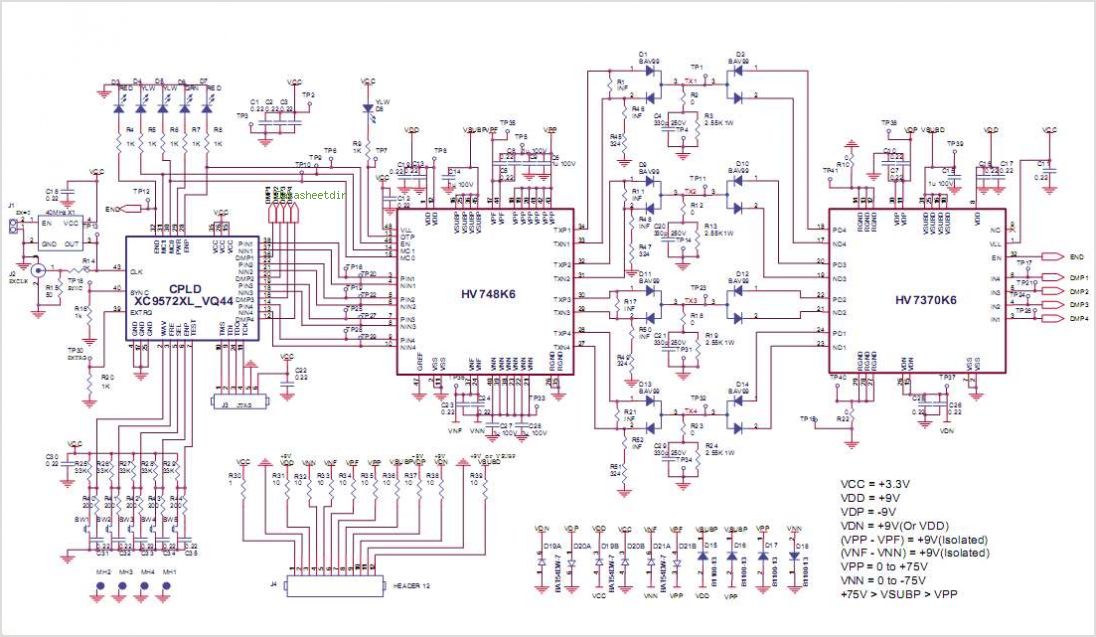
Pierce Crystal Oscillator Design

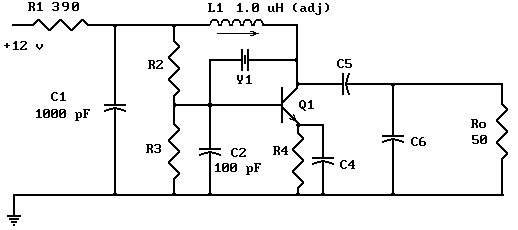
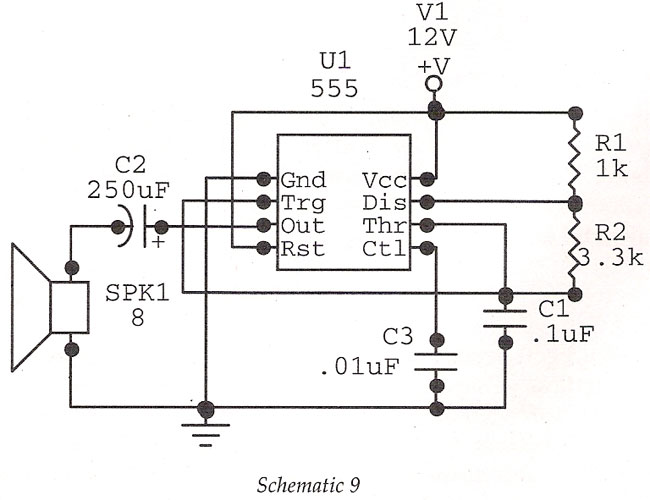
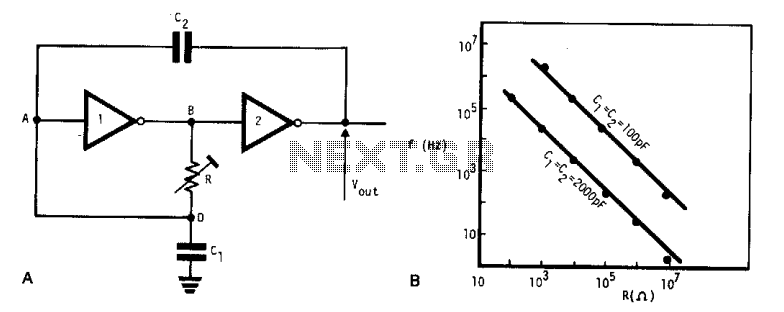
The Pierce oscillator shown above is essentially a common emitter amplifier with a tuned circuit for a collector load and a quartz crystal as a feedback element. In order to determine whether the Barkhausen criteria is satisfied, loop gain must be determined at the frequency of oscillation. This is accomplished by drawing the AC equivalent circuit of the Pierce Oscillator as shown below.

The Pierce oscillator is a type of electronic oscillator that utilizes a common emitter amplifier configuration, integrating a quartz crystal to achieve stable frequency oscillation. The circuit typically consists of a bipolar junction transistor (BJT) configured as a common emitter amplifier, which provides the necessary gain for oscillation. The collector load is formed by a tuned circuit, often comprising an inductor (L) and a capacitor (C), which together resonate at the desired frequency.

The quartz crystal acts as a frequency-selective element, ensuring that the oscillator operates at its fundamental frequency. This is critical for maintaining stability and precision in applications such as clock generation and signal processing. The feedback from the output to the input through the crystal is essential for satisfying the Barkhausen criteria, which states that the product of gain and feedback must equal one at the frequency of oscillation.

To analyze the performance of the Pierce oscillator, the AC equivalent circuit is drawn, which simplifies the assessment of the loop gain. This equivalent circuit typically includes the transistor's small-signal model, the tuned circuit, and the crystal's impedance characteristics. By calculating the loop gain at the oscillation frequency, one can confirm whether the conditions for sustained oscillation are met.

In practical implementations, additional components such as biasing resistors and coupling capacitors may be included to stabilize the operating point of the transistor and to ensure proper signal coupling between stages. The design considerations for the Pierce oscillator also involve selecting the appropriate values for the inductance and capacitance in the tuned circuit to match the crystal's resonant frequency, thus optimizing the oscillator's performance.The Pierce oscillator shown above is essentially a common emitter amplifier with a tuned circuit for a collector load and a quartz crystal as a feedback element. In order to determine whether the Barkhausen criteria is satisfied, loop gain must be determined at the frequency of oscillation.

This is accomplished by drawing the AC equivalent circuit of the Pierce Oscillator as shown below. 🔗 External reference