Clocks

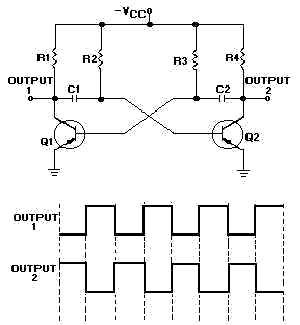
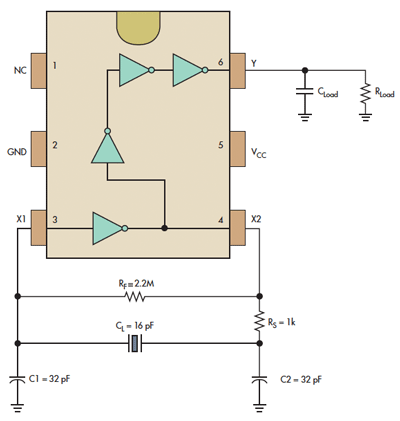
Clocks have been discussed previously in relation to their interaction with flip-flops (FFs). It is important to note that a clock generates a timing signal used to control operations. This control mechanism is evident in both D and J-K flip-flops. The clock's output must be in a specific condition for the flip-flops to function correctly. The simplest configuration is the astable or free-running multivibrator. A schematic diagram of a typical free-running multivibrator, along with its output waveforms, is provided below. This multivibrator circuit is termed "free-running" because it alternates between two distinct output voltages while active. Outputs 1 and 2 are equal and opposite as Q1 and Q2 conduct alternately. The frequency of the outputs can be modified within certain limits by adjusting the values of R2C1 and R3C2. A review of the astable multivibrator's operation can be found in NEETS, Module 9, Introduction to Wave-Generation and Wave-Shaping Circuits. Although the astable multivibrator generates a balanced square wave, it lacks the frequency stability required for some applications. The frequency stability can be enhanced by applying a trigger pulse to the circuit, with the trigger frequency needing to be higher than the free-running frequency of the multivibrator. The output frequency will align with the trigger frequency, resulting in a more stable output. Another approach to producing a stable timing pulse is to utilize a triggered monostable or one-shot multivibrator. As previously studied in NEETS, Module 9, a one-shot multivibrator has a single stable state and only changes states when triggered by an external source. A block diagram of a monostable multivibrator, including input and output signals, is presented below. The output pulse duration is determined by the charge time of an RC network within the multivibrator. Each trigger input leads to a complete output cycle, as illustrated. Trigger pulses are generated by an oscillator. The circuits described are fundamental clocks; however, as system complexity increases, so do timing requirements. Complex systems employ multiphase timing circuits to manage various operations. Multiphase units enable multiple operations to occur within a single timing cycle and allow operations to span multiple clock cycles. A block diagram of a two-phase system is depicted below, view A. The astable multivibrator provides the fundamental timing for the circuit, while one-shot multivibrators shape the pulses. Outputs Q and Q are fed into one-shot multivibrators 1 and 2, respectively. The resulting outputs are in phase with the inputs, but the pulse duration is significantly reduced, as shown in view B. Clocks are engineered for optimal equipment operation. During the design phase, the required frequency, pulse width, and number of phases are established, and the circuit is constructed to fulfill those specifications. Most modern high-speed equipment utilizes crystal-controlled oscillators as the foundation for their timing networks, as crystals maintain stability even at very high frequencies.

The astable multivibrator operates by continuously switching its output between two states, producing a square wave signal. The output frequency is influenced by the resistor-capacitor (RC) time constant, which is determined by the values of R2, C1, R3, and C2. Adjusting these components allows for fine-tuning of the frequency, making the astable multivibrator versatile for various applications.

In contrast, the triggered monostable multivibrator provides a single pulse output in response to a trigger event. This pulse duration is dictated by the RC time constant associated with the circuit, ensuring that the output pulse length is predictable and stable. The integration of an oscillator to provide trigger pulses ensures that the timing of the output is precise, which is essential for applications requiring synchronization.

For more complex systems, multiphase timing circuits are essential. These circuits can manage several tasks simultaneously, enhancing the efficiency of operations. The use of one-shot multivibrators in conjunction with an astable multivibrator allows for the shaping of output pulses, which can be crucial for applications where precise timing and pulse width modulation are necessary.

In high-speed applications, the implementation of crystal-controlled oscillators is prevalent due to their ability to maintain frequency stability across a wide range of operating conditions. The inherent stability of crystals ensures that timing circuits can operate reliably, even under high-frequency conditions, making them ideal for modern electronic systems.

Overall, the design and implementation of clock circuits, whether simple or complex, are fundamental to ensuring the proper operation of electronic devices and systems.Clocks have been mentioned in the preceding section with regard to their action with FFs. You will recall that this circuit is a timing signal generated by the equipment to control operations. This control feature is demonstrated in both the D and J-K FFs. Remember that a clocks output had to be in a certain condition for the FFs to perform their functions. The simplest form is the astable or free-running multivibrator. A schematic diagram of a typical free-running multivibrator is shown in the figure below along with its output waveforms. This multivibrator circuit is called free running because it alternates between two different output voltages during the time it is active.

Outputs 1 and 2 will be equal and opposite since Q1 and Q2 conduct alternately. The frequency of the outputs may be altered within certain limits by varying the values of R2C1 and R3C2. You may want to review the operation of the astable multivibrator in NEETS, Module 9, Introduction to Wave-Generation and Wave-Shaping Circuits.

Although the astable multivibrator circuit seems to produce a good, balanced square wave, it lacks the frequency stability necessary for some types of equipment. The frequency stability of the astable multivibrator can be increased by applying a trigger pulse to the circuit.

The frequency of the trigger must be higher than the free-running frequency of the multivibrator. The output frequency will match the trigger frequency and produce a more stable output. Another method of producing a stable timing pulse is to use a triggered monostable or one-shot multivibrator. You can recall from studying the NEETS, Module 9, that a one-shot multivibrator has one stable state and will only change states when acted on by an outside source (the trigger).

A block diagram of a monostable multivibrator with input and output signals is shown in the next figure below. The duration of the output pulse is dependent on the charge time of an RC network in the multivibrator.

Each trigger input results in a complete cycle in the output, as shown in the figure. Trigger pulses are supplied by an oscillator. The circuits described previously are very simple clocks. However, as the complexity of the system increases, so do the timing requirements. Complex systems have multiphase timing circuits to control a variety of operations. Multiphase units allow functions involving more than one operation to be completed during a single timing cycle. They also permit an operation to extend over more than one clock cycle. A block diagram of a two-phase system is shown in the next figure below, view A. The astable multivibrator provides the basic timing for the circuit, while the one-shot multivibrators are used to shape the pulses.

Outputs Q and Q are input to one-shot multivibrators 1 and 2, respectively. The resulting outputs are in phase with the inputs, but the duration of the pulse is greatly reduced as shown in view B. Clocks are designed to provide the most efficient operation of the equipment. During the design phase, the frequency, pulse width, and the number of phases required is determined; and the circuit is built to meet those requirements.

Most modern high-speed equipment uses crystal-controlled oscillators as the basis for their timing networks. Crystals are stable even at extremely high frequencies. 🔗 External reference