converting circuits to c

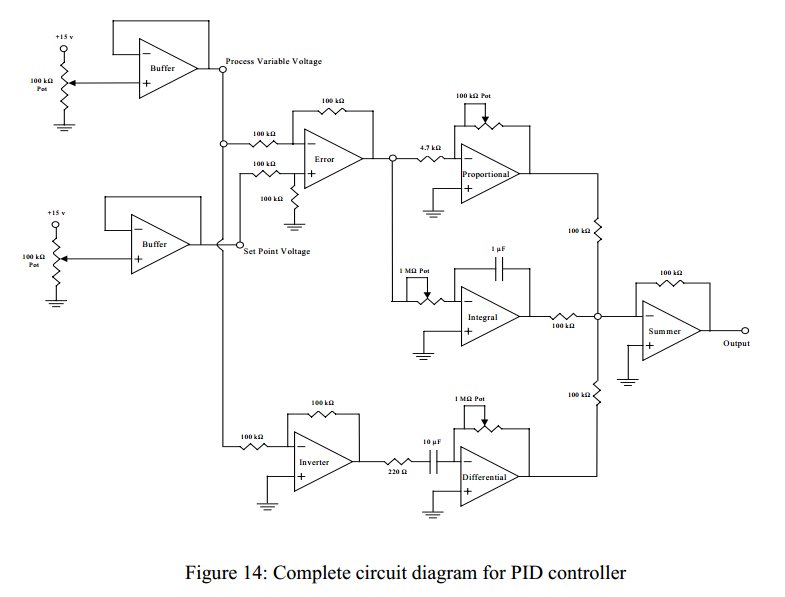
Convert a feedforward operational amplifier PID loop to C code. Assistance is needed for this conversion, as the process is unfamiliar. Input values can be obtained through an ADC, such as voltage or current, but coding a feedforward PID is a new challenge. Clarification is sought on whether "PID" is the correct terminology. The current description primarily relates to "process IDs." The context of PID here likely refers to a proportional-integral-derivative controller, and an op-amp is an operational amplifier. The inquiry pertains to coding a simulation of an operational amplifier with a feedforward loop in C. Additional information is required regarding how to approach this problem. Suggestions include creating a function that sums a function, its derivative, and its integral. However, more details are needed on how the feedforward loop is connected, along with considerations for coding. Circuit simulation languages exist, but they may be more applicable to microchip applications rather than discrete components. The initial approach may involve "s-domain circuit analysis," followed by discretization using methods like the bilinear transform to transition to the z-domain. From this point, developing the C algorithm becomes straightforward. In the PID context, "P" represents amplifying the input by a factor K, "D" involves taking successive samples from the input stream and applying weights to the last three samples, while "I" refers to a feedback loop that incorporates the last N results of the circuit with specific weights.

The task involves converting a feedforward operational amplifier PID loop into C code, which necessitates a clear understanding of both the operational amplifier's behavior and the principles of PID control. The feedforward PID controller combines three elements: proportional (P), integral (I), and derivative (D) control, which are essential for optimizing system performance.

In this context, the proportional component amplifies the error signal by a constant factor K, providing an immediate response to the current error. The integral component accumulates past errors over time, ensuring that the steady-state error is minimized. The derivative component predicts future errors based on the rate of change of the error signal, allowing the system to react more swiftly to changes.

To implement this in C, the following steps are recommended:

1. **Define Input Variables**: Establish variables to hold the input values obtained from the ADC, such as voltage and current readings.

2. **Initialize PID Parameters**: Set constants for the proportional gain (Kp), integral gain (Ki), and derivative gain (Kd). These parameters can be tuned based on the specific application requirements.

3. **Create Function for PID Calculation**: Develop a function that calculates the PID output. This function should:
- Compute the proportional term by multiplying the current error by Kp.
- Update the integral term by accumulating the error over time and multiplying it by Ki.
- Calculate the derivative term by determining the difference between the current error and the previous error, dividing it by the time elapsed, and multiplying by Kd.

4. **Implement Feedback Loop**: Integrate the PID function within a loop that continuously reads the ADC inputs, computes the PID output, and applies the output to the system (e.g., controlling a motor or adjusting a valve).

5. **Discretization**: If necessary, apply the bilinear transform to convert continuous PID parameters into discrete values suitable for implementation in the C environment.

6. **Testing and Tuning**: After coding, the system should be tested extensively to ensure stability and performance. Tuning the PID parameters may be required to achieve the desired response characteristics.

By following these steps, a comprehensive C implementation of a feedforward operational amplifier PID loop can be achieved, facilitating efficient control of various systems.Convert a feedforeward opamp PID loop to C code I am trying to do such a conversion and honestly, have no idea where to start. I can get all input values through an ADC, voltage, current, whatever, but coding a feedforeward PID is a little new to me.

Any ideas Are you sure "PID" is the right tag for your questi on Its current description is exclusively about "process IDs". Perhaps your question could be made a bit more verbose. Kerrek SB Nov 15 `12 at 19:26 PID in this context is probably a proportional-integral-differential controller. And op-amp is an operational amplifier. So, as the title suggests, the question is somehow related to how to code up a simulation of an operational amplifier with a feed-forward loop in C.

And it is sufficiently long since I last thought about these terms that I`ve not got a clue on how to go about solving the problem. Jonathan Leffler Nov 15 `12 at 19:39 @JonathanLeffler My first idea is simply making a function that sums a function, its derivative and its integral.

Isn`t that a solution user529758 Nov 15 `12 at 19:43 @H2CO3: pass ” I`d need to think harder than I`ve thought in nearly 30 years about how op-amps are characterized, and we`d need to know how the feed-forward loop is connected, and. generally, we`d need a lot more information than we have. And then there`d be issues with how to code. There are whole languages for circuit simulation, though they may be more commonly for microchip work than this which I`d characterize as `macrochip` (or discrete devices rather than a chip at all).

Jonathan Leffler Nov 15 `12 at 19:46 I think this is described first in "s-domain circuit analysis" and then the result can be discretised with eg. bilinear transform to z-domain. From that point on, the c algorithm is easy. P in the PID means amplifying input by factor K. D means taking successive samples from the input stream, multiplying them with weights b1, b2, b3 (taking e.

g. 3 last samples) and I means feedback loop, where one adds to the result N last results of the circuit again with some weights a1, a2, a3. Aki Suihkonen Nov 15 `12 at 20:31 🔗 External reference