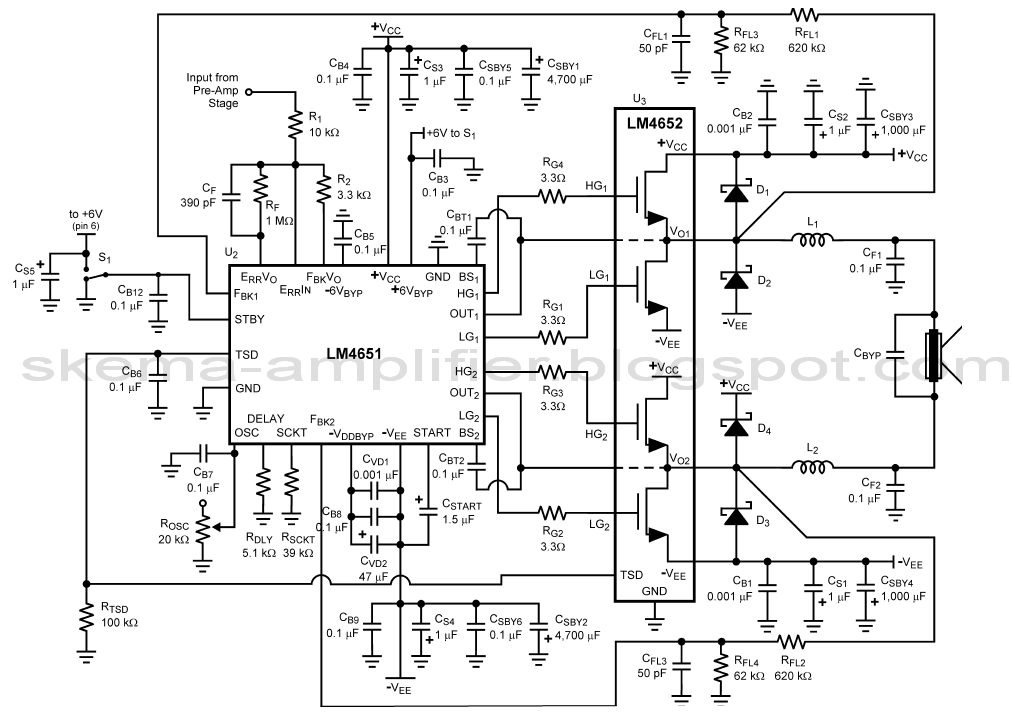
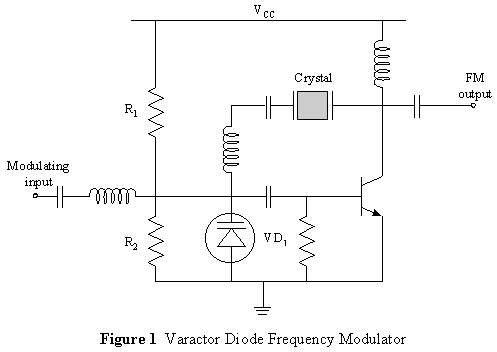
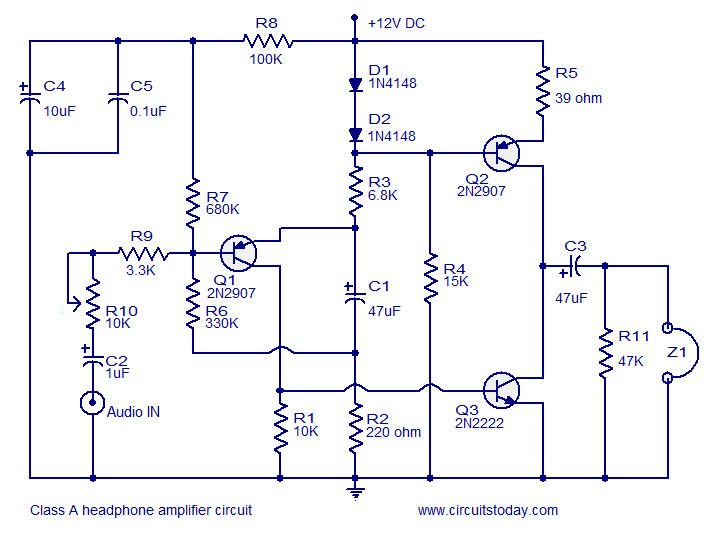
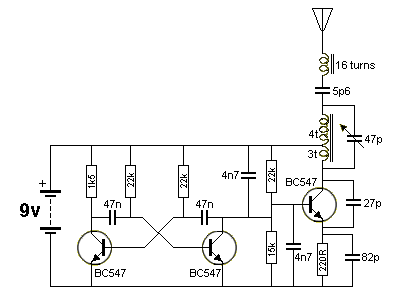
DC Circuits

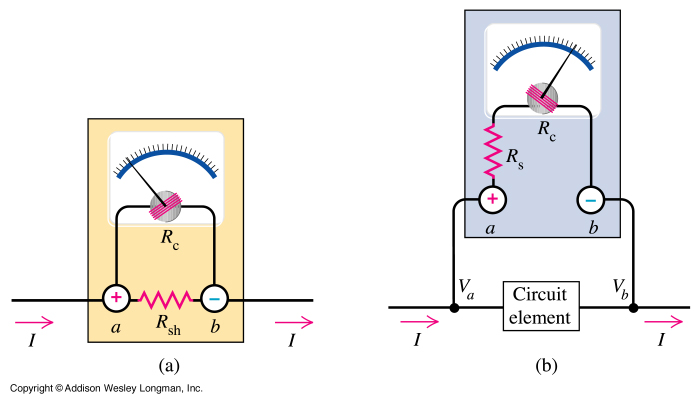
Electron trajectories in a conductor are depicted in the diagrams below. When no electric field is present inside a conducting material, electrons move randomly. However, when an electric field is applied, the electric force F = qE induces a slight drift in the motion of the electrons. It is important to note that because electrons carry a negative charge, the force F acts in a direction opposite to that of the electric field E. Additionally, the motion of an electron in a metallic conductor under the influence of an electric field can be compared to a ball rolling down an inclined plane and bouncing off pegs in its path. Electric charges traverse a material in a similar manner. If the charge's motion is severely restricted, the material is said to exhibit high electrical resistance. The resistance of a material is influenced by the arrangement or spacing of its atoms or molecules. The atomic motion directly impacts the electrical resistance; increased atomic vibration generally leads to higher resistance. As temperature rises, molecular vibrations intensify, resulting in increased electrical resistance. This temperature-induced resistance variation is quantified by a factor known as the temperature coefficient of resistivity (resistivity being closely related to resistance). Other factors affecting the resistance of an electrical conductor include its length and cross-sectional area. A longer conductor exhibits greater resistance, while a larger cross-sectional area reduces resistance. These principles can be expressed mathematically in the equation R = ρL/A, where R represents resistance, ρ is the resistivity (a material-dependent constant), L is the length of the conductor, and A is its cross-sectional area. The resistivity varies with the material characteristics and temperature, typically measured in ohm-meters. The relationship between resistance (R) or resistivity (ρ) and temperature is generally linear over limited temperature ranges and can be represented by the equation: R(T) = R₀(1 + α(T - T₀)), where T is the temperature in Celsius, T₀ is a reference temperature (commonly room temperature or 20 degrees Celsius), R₀ is the resistance at the reference temperature, and α is the temperature coefficient of resistivity in units of 1/°C. Laboratory measurements will be conducted to observe the variation of resistance with temperature and verify the accuracy of this equation. Current flows through a conductor from a region of higher electric potential (voltage) to a region of lower electric potential, akin to water flowing downhill from a higher potential energy to a lower one. The greater the electric potential difference across the conductor, the larger the current that flows through it. This difference in voltage is commonly referred to as voltage. When the current in a conductor is directly proportional to the potential difference (voltage) driving it, Ohm's Law is satisfied: V = IR, where R, the resistance of the conductor, serves as the proportionality constant or the slope of the V vs. I graph.

The behavior of electrons in a conductor under the influence of an electric field is a fundamental concept in electronics. The random motion of electrons in the absence of an electric field illustrates the intrinsic nature of charge carriers in conductive materials. The introduction of an electric field results in a net drift velocity, which is critical for the conduction of electricity. The analogy of a ball rolling down an inclined plane effectively captures the essence of this drift, emphasizing how external forces influence the motion of charged particles.

The concept of electrical resistance is pivotal in understanding how materials respond to electric currents. The arrangement of atoms within a conductor determines how easily electrons can move through it. As temperature increases, the increased kinetic energy of the atoms leads to more frequent collisions with electrons, thereby increasing resistance. This relationship is quantitatively described by the temperature coefficient of resistivity, which allows for predictions about how a material will behave under varying thermal conditions.

The mathematical formulation of resistance, R = ρL/A, encapsulates the relationship between resistance, resistivity, length, and cross-sectional area, providing a clear framework for analyzing different conductive materials. The resistivity, a material-specific property, varies with temperature, necessitating careful consideration in circuit design and material selection.

Ohm's Law further elucidates the relationship between voltage, current, and resistance, forming the foundation for circuit analysis. The linear relationship depicted in V vs. I graphs serves as a practical tool for engineers to evaluate the performance of electrical components. Understanding these principles is essential for designing efficient circuits and systems, ensuring optimal performance in various applications.Electron trajectories in a conductor are shown in the diagrams below. If there is no electric field inside a conducting material electrons move randomly. If a field is present the electric force F=qE imposes a small drift on the electron`s motion. Note that since the electron has a negative charge the force F is in a direction opposite to the field E. rolling down an inclined plane and bouncing off pegs in its path is analogous to the motion of an electron in a metallic conductor with an electric field present. Electric charges move through a material in a similar way. If the charge has its motion greatly restricted we say the material through which it is moving has a large electrical RESISTANCE.

The resistance of a material depends on the arrangement, or spacing, of the atoms or molecules in the material. The motion of the atoms affects the electrical resistance of the material. If the atoms or molecules vibrate a lot, in general, they will increase the resistance of the material.

And since we know that as the temperature rises molecules vibrate more and more, we conclude that the electrical resistance of a material is increased as the temperature rises. The amount of electrical resistance caused by a temperature increase is described by factor (a) called the temperature coefficient of resistivity (resistivity is closely related to resistance).

Other factors that affect the resistance of an electrical conductor are its length and cross-sectional area. The longer the conductor the greater the resistance, and the greater the cross-section area through which the charges flow the smaller the resistance of the conductor.

We can formulate these ideas in an equation relating the resistance, the resistivity, the length, and the area of a conductor. Since the resistance is proportional to the length and inversely proportional to the area we can say that R = r L / A, where we have inserted a constant of proportionality called the resistivity (r).

The resistivity is dependent on the characteristics of the material and its temperature and is, in general, different for each material (in units of ohm-meters). The dependence of resistance (R) or resistivity (r) on temperature has been found to be linear over limited temperature ranges and can be described as a straight line: where T is the Celsius temperature, To is the reference temperature (usually room temperature or 20 degrees C), Ro is the resistance at the reference temperature, and a is the temperature coefficient of resistivity in units of 1/degrees C.

You will measure the variation of resistance with temperature in the lab and verify the accuracy of this equation. Current through a conductor flows from a higher electric potential (or voltage) to a lower electric potential; just as water flows from a higher level of potential energy to a lower level of potential energy, i.

e. , downhill! The greater the electric potential between the ends of a conductor, the greater the current through the conductor. The difference in voltage levels is often referred to as the voltage. If the current in a conductor is proportional the the potential difference (or voltage) driving the current through the conductor we say that Ohm`s Law is obeyed: V = I R, where R, the resistance of the conductor, is the constant of proportionality or the slope of the V vs.

I graph. See the V vs. I graphs below. Not all o 🔗 External reference