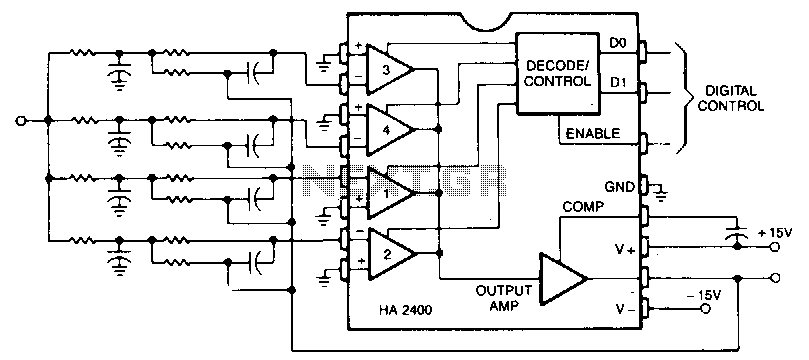
Frequencies and Filters
One of the limitations affecting all real amplifiers is the finite signal bandwidth. This implies that any amplifier constructed or utilized has an upper limit to the range of sinewave frequencies it can amplify. Consequently, high-frequency signals may not be boosted and could instead be attenuated. Additionally, high-frequency signals may become distorted, altering their wave shape. Some amplifiers also have low-frequency limitations and cannot amplify frequencies below a certain threshold. It is essential to assess these effects to determine if a specific amplifier is suitable for a particular application. Furthermore, there are situations where it is necessary to intentionally modify the signal frequencies that a system will pass or amplify, necessitating deliberate filtering. Common examples include tone controls or equalization (EQ) controls, which are employed to adjust the overall tonal balance of sound signals or to correct for unwanted frequency-dependent effects. The effect of a filter is typically described in terms of frequency response, which defines the filter's behavior regarding its gain as a function of frequency. A typical example is illustrated in Figure 3.1, showing the measured power gain (or loss) as a function of frequency for a specific low-pass filter. This example is based on a commercial audio filter sold under the Toko brand name for use in hi-fi equipment. This filter is passive, meaning it contains no gain devices, only passive components such as resistors, capacitors, or inductors. Consequently, any unwanted losses in the filter must be counteracted. The overall circuit measured in this case is depicted in Figure 3.2, where the filter is positioned between two amplifiers that elevate the signal level. In this example, the filter's role is to prevent high frequencies from reaching the output, which is to be sampled by an ADC. The overall voltage gain is approximately G = 50 at 1 kHz. The Toko filter allows signals from direct current (DC) up to around 18 kHz to pass while attenuating higher frequencies. Although the frequency response displayed in Figure 3.1 is a common method for illustrating a filter's behavior, it does not capture the entire picture. As sinewave components traverse the filter, they may experience a delay that varies with frequency. This phenomenon is often represented through a plot of phase delay as a function of signal frequency. For the same filter, the measured phase delay as a function of frequency is illustrated in Figure 3.3. In this figure, the phase appears to fluctuate in a complex manner; however, the underlying behavior is simpler than it seems, attributable to two primary reasons.
The finite signal bandwidth of amplifiers is a crucial consideration in electronic circuit design. Understanding the limitations of frequency response allows engineers to select appropriate amplifiers for specific applications, ensuring optimal performance. The Toko low-pass filter serves as a practical example of how passive components can be employed to manage frequency response effectively. In audio applications, this filter is integrated between amplifiers to prevent high-frequency noise from interfering with the signal intended for analog-to-digital conversion (ADC).
The frequency response curve provides insight into how the filter affects signal gain across a spectrum of frequencies, while the phase delay information reveals how different frequency components are shifted in time as they pass through the filter. This delay can impact the overall performance of audio systems, particularly in applications where phase coherence is critical.
To analyze the performance of such filters, it is essential to consider both the magnitude response and the phase response. Engineers often utilize simulation tools and measurement equipment to evaluate these characteristics, ensuring that the design meets the intended specifications. The interplay between gain and phase response informs decisions regarding the integration of additional signal processing elements, such as equalizers or dynamic range compressors, to achieve the desired audio quality.
In summary, a thorough understanding of amplifier bandwidth limitations, filter design, and frequency response is vital for engineers working in audio and signal processing fields. By carefully considering these factors, it is possible to create systems that deliver high-quality, distortion-free audio signals while maintaining the integrity of the original sound.One of the limitations which affect all real amplifiers is that they all have a finite Signal Bandwidth. This means that whatever amplifier we build or use, we find that there is always an upper limit to the range of sinewave frequencies it can amplify.
This usually means that high frequencies signals won`t be boosted, and may attenuated instead. It also often means that high frequency signals may be Distorted i. e. their waveshape may be changed. Some amplifiers also have a low-frequency limitation as well, and are unable to amplify frequencies below some lower limit. We therefore need to be aware of, and be able to assess, these effects to decide if a specific amplifier is suitable for a given task.
In addition to the above, there are many situations where we deliberately want to alter the signal frequencies a system will pass on or amplify. There are many situations where deliberate filtering is needed. Some common examples are: Tone Controls` or EQ` (Equalisation) controls. These tend to be used to alter the overall tonal balance of sound signals, or correct for other unwanted frequency-dependent effects.
The most common and most obvious way to describe the effect of a filter is in terms of is Frequency Response. This defines the filter`s behaviour in terms of its Gain as a function of frequency. figure 3 ·1 shows a typical example. In this case Figure 3 ·1 shows the measured power gain (or loss!) as a function of frequency for a specific low-pass filter.
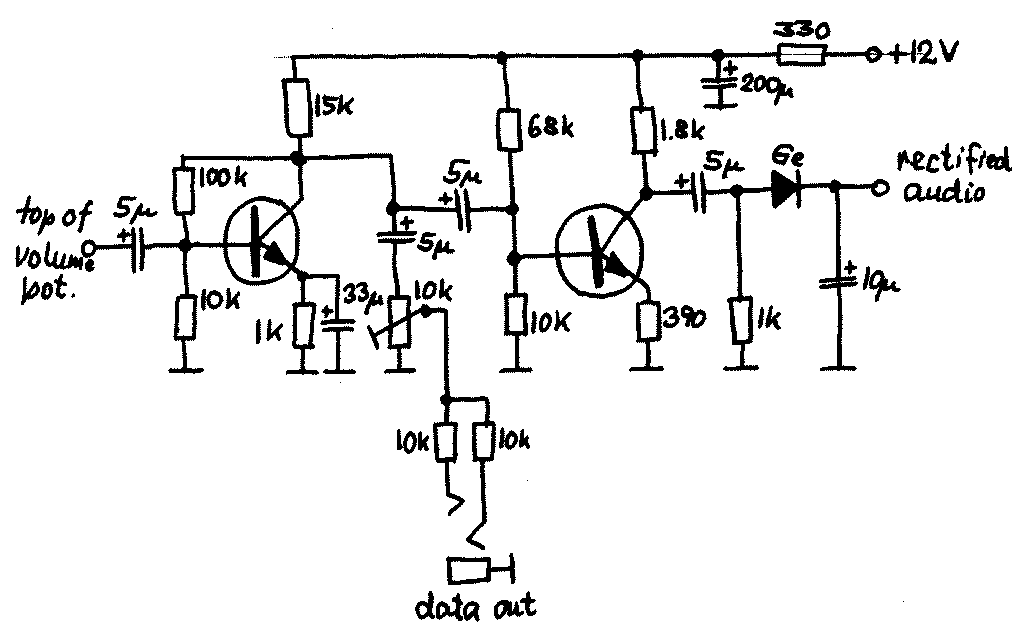
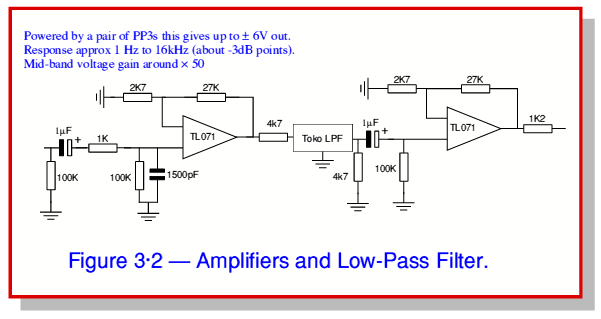
This example is based upon a commercial audio filter sold under the Toko` brand name for use in hi-fi equipment. This filter is Passive i. e. includes no gain devices, just passive components like resistors, capacitors, or inductors. As a result we need to counteract any unwanted losses in the filter. The overall circuit measured in this case is shown in figure 3 ·2. Here the filter actually sits in between two amplifiers which raise the signal level. The filter`s job in the system this example is taken from is to stop high frequencies from reaching the output which is to be sampled by an ADC.
The overall voltage gain is around G—50 at 1 kHz. The Toko filter passes signals from d. c. up to around 18 kHz but attenuates higher frequencies. Note also the pair of Although a frequency response of the kind shown in figure 3 ·1 is the most common way to display the behaviour of a filter, it doesn`t tell the whole story. When sinewave components pass through the filter they may also be delayed by an amount that depends upon their frequency.
This effect is often represented in terms of a plot of the Phase Delay as a function of signal frequency. For the same filter as before the measured Phase Delay as a function of frequency is shown in figure 3 ·3.
In figure 3 ·3 the phase seems to jump around` in quite a complex way. However the underlying behaviour is simpler than it appears. There are two reasons for this. 🔗 External reference
The finite signal bandwidth of amplifiers is a crucial consideration in electronic circuit design. Understanding the limitations of frequency response allows engineers to select appropriate amplifiers for specific applications, ensuring optimal performance. The Toko low-pass filter serves as a practical example of how passive components can be employed to manage frequency response effectively. In audio applications, this filter is integrated between amplifiers to prevent high-frequency noise from interfering with the signal intended for analog-to-digital conversion (ADC).
The frequency response curve provides insight into how the filter affects signal gain across a spectrum of frequencies, while the phase delay information reveals how different frequency components are shifted in time as they pass through the filter. This delay can impact the overall performance of audio systems, particularly in applications where phase coherence is critical.
To analyze the performance of such filters, it is essential to consider both the magnitude response and the phase response. Engineers often utilize simulation tools and measurement equipment to evaluate these characteristics, ensuring that the design meets the intended specifications. The interplay between gain and phase response informs decisions regarding the integration of additional signal processing elements, such as equalizers or dynamic range compressors, to achieve the desired audio quality.
In summary, a thorough understanding of amplifier bandwidth limitations, filter design, and frequency response is vital for engineers working in audio and signal processing fields. By carefully considering these factors, it is possible to create systems that deliver high-quality, distortion-free audio signals while maintaining the integrity of the original sound.One of the limitations which affect all real amplifiers is that they all have a finite Signal Bandwidth. This means that whatever amplifier we build or use, we find that there is always an upper limit to the range of sinewave frequencies it can amplify.
This usually means that high frequencies signals won`t be boosted, and may attenuated instead. It also often means that high frequency signals may be Distorted i. e. their waveshape may be changed. Some amplifiers also have a low-frequency limitation as well, and are unable to amplify frequencies below some lower limit. We therefore need to be aware of, and be able to assess, these effects to decide if a specific amplifier is suitable for a given task.
In addition to the above, there are many situations where we deliberately want to alter the signal frequencies a system will pass on or amplify. There are many situations where deliberate filtering is needed. Some common examples are: Tone Controls` or EQ` (Equalisation) controls. These tend to be used to alter the overall tonal balance of sound signals, or correct for other unwanted frequency-dependent effects.
The most common and most obvious way to describe the effect of a filter is in terms of is Frequency Response. This defines the filter`s behaviour in terms of its Gain as a function of frequency. figure 3 ·1 shows a typical example. In this case Figure 3 ·1 shows the measured power gain (or loss!) as a function of frequency for a specific low-pass filter.
This example is based upon a commercial audio filter sold under the Toko` brand name for use in hi-fi equipment. This filter is Passive i. e. includes no gain devices, just passive components like resistors, capacitors, or inductors. As a result we need to counteract any unwanted losses in the filter. The overall circuit measured in this case is shown in figure 3 ·2. Here the filter actually sits in between two amplifiers which raise the signal level. The filter`s job in the system this example is taken from is to stop high frequencies from reaching the output which is to be sampled by an ADC.
The overall voltage gain is around G—50 at 1 kHz. The Toko filter passes signals from d. c. up to around 18 kHz but attenuates higher frequencies. Note also the pair of Although a frequency response of the kind shown in figure 3 ·1 is the most common way to display the behaviour of a filter, it doesn`t tell the whole story. When sinewave components pass through the filter they may also be delayed by an amount that depends upon their frequency.
This effect is often represented in terms of a plot of the Phase Delay as a function of signal frequency. For the same filter as before the measured Phase Delay as a function of frequency is shown in figure 3 ·3.
In figure 3 ·3 the phase seems to jump around` in quite a complex way. However the underlying behaviour is simpler than it appears. There are two reasons for this. 🔗 External reference
Related Circuits
The disadvantages of pi-filters include higher costs, increased weight, larger size, and the external magnetic field generated by the series inductor. These issues can be mitigated by substituting the series inductor with a series resistor, referred to as an...
From the discussion made so far on the filters, it can be concluded that in the stopband, the gain of the filter changes at the rate of 20 dB/decade for first-order filters and 40 dB/decade for second-order filters. This...
This circuit features a ceramic filter integrated with an FM intermediate frequency (IF) amplifier. The FM IF amplifier circuit primarily consists of an input variable voltage regulator (T), ceramic filters (CF1), and additional components such as the IF amplifier...
A band-pass filter is a circuit designed to pass signals only within a specific band of frequencies while attenuating all signals outside this range. The key parameters of a band-pass filter include the high and low cut-off frequencies (fH...
This is a second-order low-pass filter with a programmable cutoff frequency. The circuit should be driven from a low-source impedance, as there are paths from the output to the input through the unselected networks. Virtually any filter function that...
This option has the advantage that one does not need to change anything in the receiver itself. However, since any filter will give some attenuation of the signal, this will degrade the noise figure of the receiver and thus...