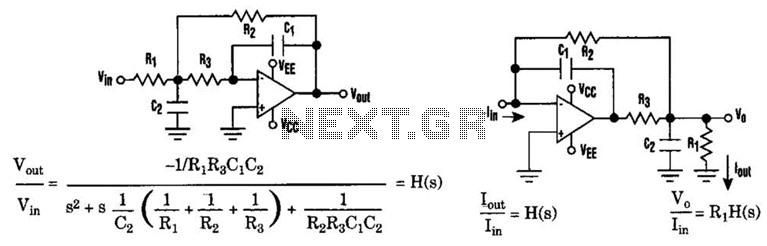
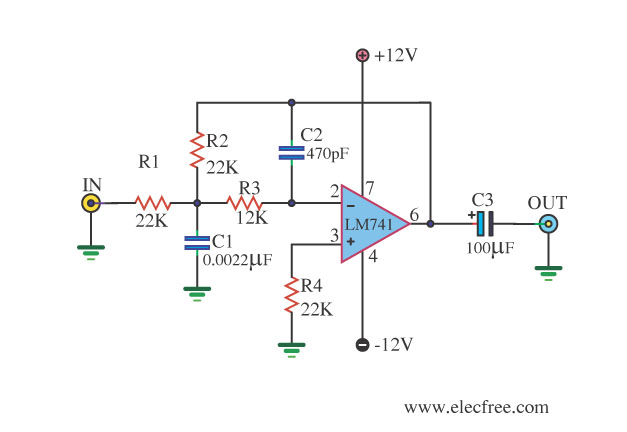
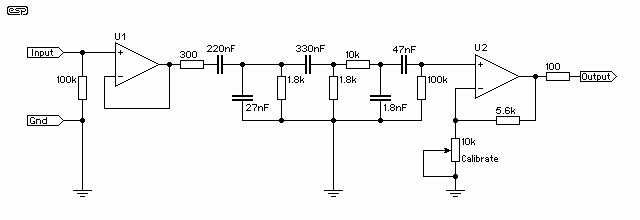
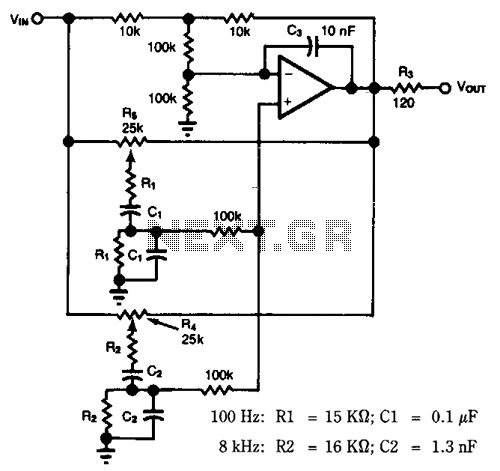
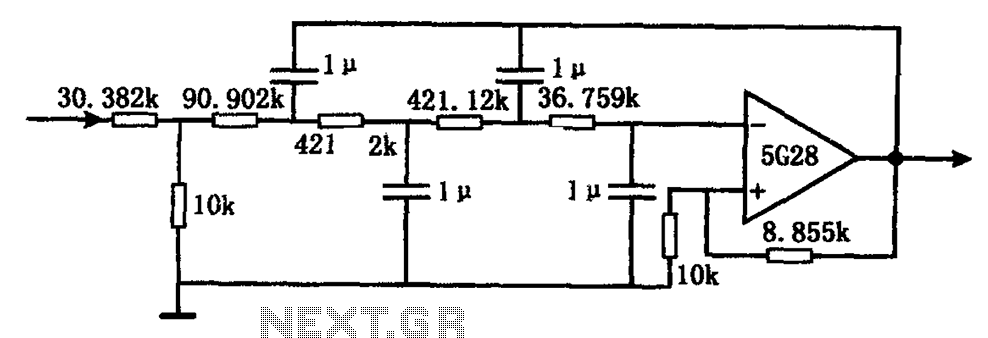
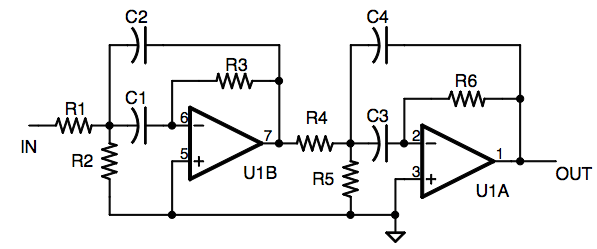
Low-pass filter

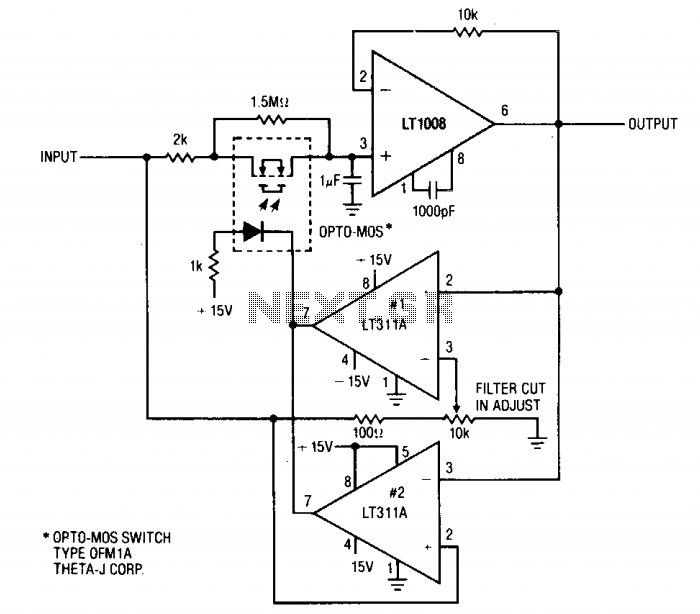
This circuit is useful where fast signal acquisition and high precision are required, such as in electronic scales. The filter's time constant is determined by the 2-ohm resistor and the 1 µF capacitor until comparator No. 1 activates. After this point, the time constant is established by the 1.5-ohm resistor and the 1 µF capacitor. Comparator No. 2 facilitates a rapid reset. The circuit reaches a final value three times faster than a basic 1.5-ohm and 1 µF filter, exhibiting minimal DC error.

This circuit is designed for applications demanding rapid signal processing and high accuracy, particularly in the context of electronic weighing systems. The initial configuration employs a 2-ohm resistor in conjunction with a 1 µF capacitor to create a low-pass filter with a specific time constant, which governs the response time of the circuit until comparator No. 1 engages. The time constant, defined as τ = R × C, results in a response time that allows for quick signal acquisition.

Upon activation of comparator No. 1, the circuit transitions to a secondary configuration where a 1.5-ohm resistor and a 1 µF capacitor replace the initial components. This modification further enhances the speed of the circuit, allowing it to stabilize at a final output value significantly quicker than a standard filter setup with the same capacitance but a higher resistance value, such as the 1.5-ohm and 1 µF combination. The circuit's design minimizes DC error, ensuring that the output closely reflects the actual input signal without significant drift or offset.

Additionally, comparator No. 2 plays a crucial role in the circuit by providing a rapid reset function. This feature is essential for applications where continuous operation and quick recovery from transient states are necessary. The overall performance of this circuit makes it highly suitable for precision measurement devices, where both speed and accuracy are critical parameters. The design considerations and component selections reflect a careful balance between response time and signal fidelity, resulting in an effective solution for high-performance electronic scales.This circuit is useful where fast signal acquisition and high precision are required, as in electronic scales. The filter's time constant is set by the 2 ohm resistor and the 1 µ capacitor until comparator No. 1 switches. The time constant is then set by the 1.5 ohm resistor and the 1 jtF capacitor. Comparator No. 2 provides a quick reset. The circuit settles to a final value three times as fast as a simple 1.5 ohm—1 µ¥ filter, with almost no dc error. 🔗 External reference