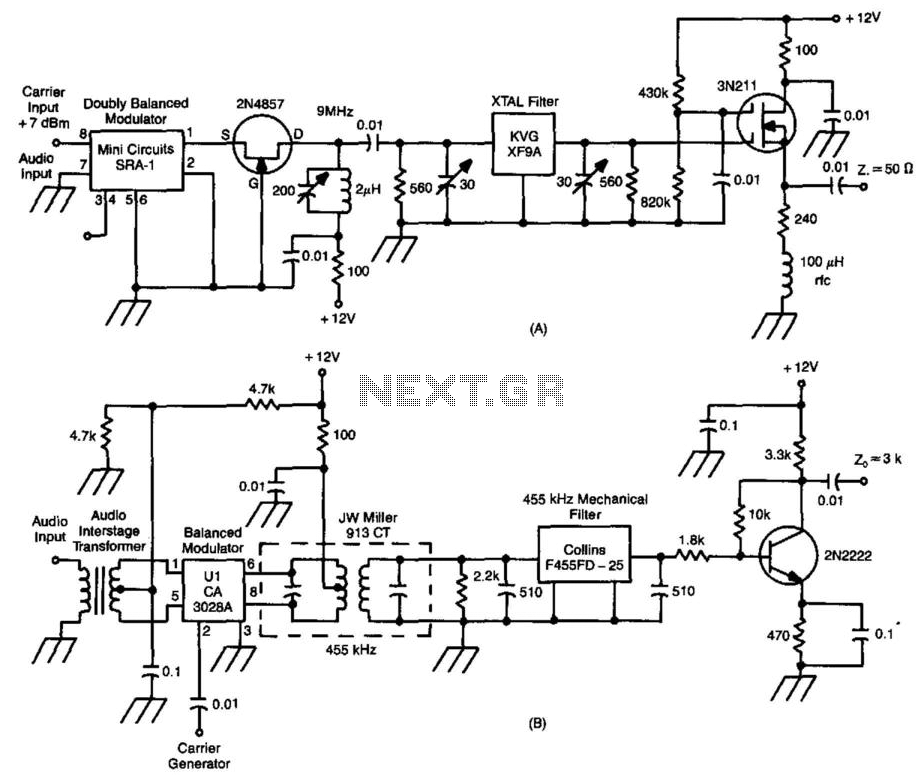
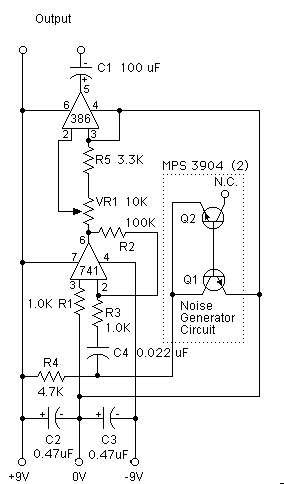
Marx Generators

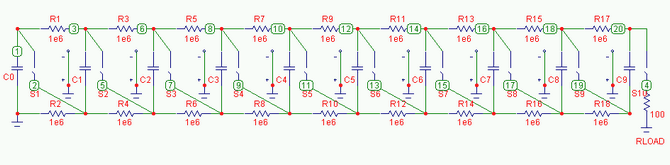
Marx Generators are commonly utilized in pulsed power and high voltage applications to produce a high peak voltage pulse. The fundamental principle behind these generators involves charging several capacitors in parallel, followed by closing switches to connect them in series. This configuration allows the charge voltages to sum up, resulting in an output voltage approximately equal to NVo, where N represents the number of Marx stages, and Vo denotes the initial charging voltage. In low repetition rate applications, resistors serve as charging isolation components. However, in high repetition rate scenarios, the power dissipation in these components becomes excessively high, necessitating the use of inductors. A circuit schematic for a 10-stage Marx generator is presented below. In this model, each stage capacitor has a capacitance of 100nF and is charged to a voltage of 10 kV. At 1 ms into the simulation, all stage switches close, allowing the Marx generator to operate by connecting each capacitor in series. The resulting equivalent series capacitance is 10nF, which then discharges into a load resistor, producing a peak voltage of 100 kV. The voltage across the 100-ohm load resistor (V(RLOAD)) is displayed after the Marx generator fully erects, while the circuit current (I(RLOAD)) is illustrated in the second, lower plot.

The Marx generator operates on the principle of voltage multiplication through a series of stages, each consisting of a capacitor and a switch. In the described 10-stage configuration, the capacitors are charged to a predetermined voltage before the switches are activated. This activation occurs at a specific time in the simulation, which demonstrates the generator's ability to rapidly transition from a charged state to a high-voltage output state. The initial charging voltage (Vo) of 10 kV per stage results in a total output voltage of 100 kV when all capacitors are connected in series.

In practical applications, the choice between resistors and inductors for charging isolation is critical. Resistors, while effective in low-frequency applications, can generate significant heat due to power dissipation at high frequencies, thereby reducing efficiency. Inductors, on the other hand, are preferred in high repetition rate scenarios as they can handle higher power levels with less heat generation, thus maintaining system reliability.

The load resistor in this configuration is crucial for dissipating the energy stored in the capacitors upon discharge. The 100-ohm load resistor is selected to allow for a controlled discharge, providing a clear measurement of the voltage and current waveforms produced by the Marx generator. The voltage across the load resistor (V(RLOAD)) and the current through it (I(RLOAD)) are essential parameters for evaluating the performance of the generator and its suitability for specific applications in pulsed power technology.Marx Generators are often used in pulsed power and high voltage applications to generate a high peak voltage pulse. The simplified theory behind them is that a number of capacitors are charged in parallel and then switches are closed to connect them in series with the charge voltage adding up so that the output voltage is approximately equal to NVo with N being the number

of Marx stages and Vo being the initial charging voltage. In low rep-rate applications, resistors are used as charging isolation components. In high rep-rate applications, the power dissipation within these elements becomes unacceptably large and inductors must be utilized. The circuit schematic for a 10 stage Marx generator is shown below. In this specific model, each stage capacitor is 100nF and is charged to 10 kV. At 1 ms into the simulation, each of the stage switches close and the Marx erects, connecting each capacitor in series.

The equivalent series capacitance (10nF) then discharges into the load resistor with a peak voltage of 100 kV. The results of the circuit model are shown below. V(RLOAD) is the voltage on the 100 ohm load resistor after the Marx fully erects. The circuit current, I(RLOAD) is graphed in the second, lower plot. 🔗 External reference