Milliamp Meter to Voltmeter

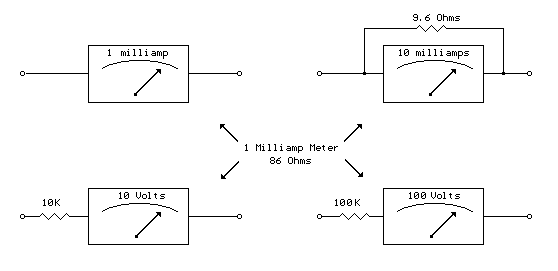
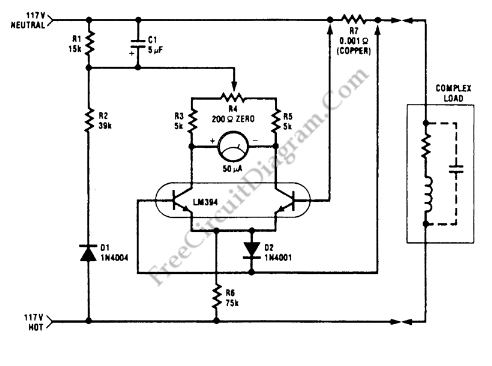
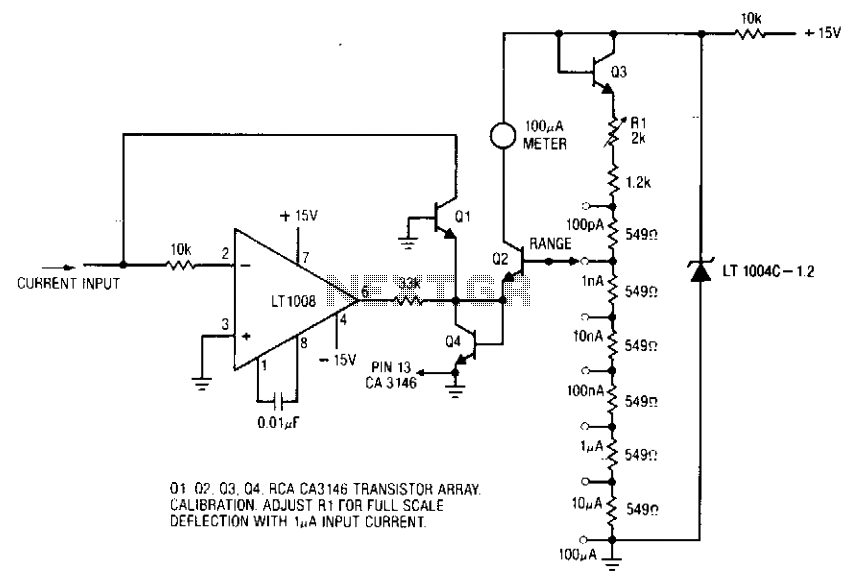
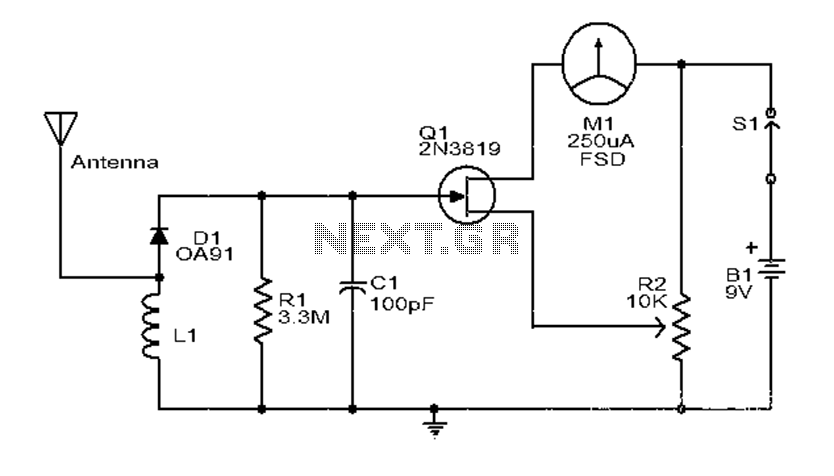
A milliamp meter can be used as a volt meter by adding a series resistance. The resistance needed is the full scale voltage reading divided by the full scale current of the meter movement. So, if you have a 1 milliamp meter and you want to read 0-10 volts you will need a total resistance of 10/.001 = 10K ohms. The meter movement itself will have a small resistance which will be part of the total 10K resistance, but it is usually low enough to ignore. The meter in the example below has a resistance of 86 ohms so the true resistor value needed would be 10K-86 or 9914 ohms. More: But using a 10K standard value will be within 1% so we can ignore the 86 ohms. For a full scale reading of 1 volt, the meter resistance would be more significant since it would be about 8% of the total 1K needed, so you would probably want to use a 914 ohm resistor, or 910 standard value. The milliamp meter can also be used to measure higher currents by adding a parallel resistance. The meter resistance now becomes very significant since to increase the range by a factor of ten, we need to bypass 9/10 of the total current with the parallel resistor. So, to convert the 1 milliamp meter to a 10 milliamp meter, we will need a parallel resistor of 86/9 = 9.56 ohms.

A milliamp meter, typically designed for measuring small currents, can be adapted for voltage measurement by incorporating a series resistor. The calculation for the required resistance is based on the desired full-scale voltage and the full-scale current rating of the meter. For example, a 1 milliamp meter configured to measure up to 10 volts necessitates a series resistance of 10,000 ohms (10V / 0.001A).

The internal resistance of the meter movement, while present, is often negligible in this context. In the cited case, the meter's internal resistance is 86 ohms, which results in a calculated required resistance of 9,914 ohms (10,000 ohms - 86 ohms). However, for practical purposes, utilizing a standard 10K ohm resistor suffices as it falls within a 1% tolerance, allowing for the internal resistance to be disregarded.

In scenarios where the meter is used for lower voltage measurements, such as a full-scale reading of 1 volt, the internal resistance becomes more relevant, accounting for approximately 8% of the total resistance needed. In such cases, a resistor value of 914 ohms or the nearest standard value of 910 ohms should be employed to ensure accuracy.

Furthermore, the milliamp meter can also be modified to measure higher currents by adding a parallel resistor. This adjustment is crucial as it allows the meter to bypass a significant portion of the current, effectively increasing its range. For instance, to convert a 1 milliamp meter to a 10 milliamp meter, a parallel resistor of approximately 9.56 ohms is required, calculated from the ratio of the internal resistance to the desired current increment (86 ohms / 9).

In summary, by strategically selecting series and parallel resistors, a milliamp meter can be effectively repurposed for both voltage and higher current measurements, expanding its functionality while maintaining measurement accuracy.A milliamp meter can be used as a volt meter by adding a series resistance. The resistance needed is the full scale voltage reading divided by the full scale current of the meter movement. So, if you have a 1 milliamp meter and you want to read 0-10 volts you will need a total resistance of 10/.001 = 10K ohms.

The meter movement itself will have a small resistance which will be part of the total 10K resistance, but it is usually low enough to ignore. The meter in the example below has a resistance of 86 ohms so the true resistor value needed would be 10K-86 or 9914 ohms.

But using a 10K standard value will be within 1% so we can ignore the 86 ohms. For a full scale reading of 1 volt, the meter resistnace would be more significant since it would be about 8% of the total 1K needed, so you would probably want to use a 914 ohm resistor, or 910 standard value. The milliamp meter can also be used to measure higher currents by adding a parallel resistance. The meter resistance now becomes very significant since to increase the range by a factor of ten, we need to bypass 9/10 of the total current with the parallel resistor.

So, to convert the 1 milliamp meter to a 10 milliamp meter, we will need a parallel resistor of 86/9 = 9.56 ohms. 🔗 External reference