Precision Triangular-Wave Generator Uses a Single IC

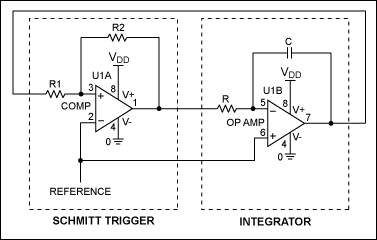
This application note describes the implementation of a single-supply triangular wave oscillator using the MAX9000 integrated circuit and several passive components. The circuit employs an operational amplifier, a comparator, and a voltage reference as the main active components. The MAX9000 is selected for its integration of these three elements. The linearity of triangular waveforms makes them beneficial in various "sweep" circuits and testing equipment. For instance, triangular wave oscillators are commonly used in pulse width modulation (PWM) circuits within switched-mode power supplies and induction motor control systems. This article details a compact triangular wave oscillator utilizing a single MAX9000 IC alongside passive components. The MAX9000 device family includes a high-speed operational amplifier, a high-speed comparator, and a precision bandgap reference. Figure 1 illustrates a basic triangular wave generator circuit, which consists of two primary building blocks: an integrator that produces the triangular wave output and a comparator with external hysteresis (Schmitt trigger) to define the desired amplitude of the triangular wave. The operational amplifier is configured as an integrator to generate the triangular output, based on the principle that integrating a constant voltage results in a linear ramp. The output of the integrator is fed back to its inverting input via a Schmitt trigger, with the input threshold voltages designed to switch states according to the desired peak voltages of the triangular wave output. A limitation of the circuit in Figure 1 is that the peaks of the triangular wave can only be symmetric around the reference voltage applied to the inverting input of the comparator. To produce a triangular wave ranging from 0.5V to 4.5V, a reference voltage of (0.5V + 4.5V)/2 = 2.5V is necessary. Since a standard bandgap reference outputs 1.23V, it is advantageous to allow the triangular wave's voltage range to be independent of the bandgap reference. This flexibility is achieved by including resistor R3 in the hysteresis network, as shown in Figure 2, which employs the MAX9000. Resistor R3 allows the peaks of the triangular wave to be set independently of the reference voltage. The input bias current at the comparator's CIN+ terminal is less than 80nA. To reduce errors resulting from the input bias current, the current through resistor R2 should be at least 8 µA, calculated using the formula (VREF - VOUT)/R2. Two potential output states yield two equations for R2; the smaller of the two calculated values should be selected. For instance, with VDD = 5V, VREF = 1.23V, and IR2 = 8 µA, the two values for R2 are 471.25kΩ and 153.75kΩ. Therefore, a standard value of 154kΩ is chosen for R2. During the rising ramp of the triangular wave, the output of the comparator is triggered low (VSS), while the falling ramp requires the output to be at logic high (VDD). The comparator must switch states at the necessary peak and valley points of the triangular wave. Nodal analysis at the noninverting input of the comparator enables the derivation of two simultaneous equations for these thresholds. In this scenario, the voltage range of the triangular wave is from 0.5V to 4.5V, leading to the substitution of VIH = 4.5V, VIL = 0.5V, VDD = 5V, and VREF = 1.23V, resulting in R1 = 124kΩ and R3 = 66.5kΩ. The maximum input bias current of the operational amplifier is 2nA, necessitating that the current through R4 remains above 0.2 µA to minimize errors. For this example, a frequency of f = 25kHz, VOUT, P-P = 4V (for the triangular wave from 0.5V to 4.5V), and VREF = 1.23V are selected, yielding a time constant of R4 × C = 9.27 µs. Choosing C = 220pF and R4 = 42.2kΩ will ensure that the output frequency aligns with the design specifications, provided the operational amplifier is not slew limited.

The circuit design for the triangular wave oscillator is centered around the MAX9000, which integrates essential components for generating the triangular waveform. The operational amplifier is configured in an integrator configuration, where the output voltage ramps up linearly in response to a constant input voltage. This linear ramp is crucial for producing the triangular wave output. The Schmitt trigger comparator introduces hysteresis, allowing for stable switching at the defined peak and valley voltages of the triangular waveform.

The selection of resistors R2, R3, and R4, along with the capacitor C, is critical to achieving the desired frequency response and waveform characteristics. The choice of standard resistor values ensures availability and ease of implementation. The feedback mechanism through the hysteresis network allows for independent control of the triangular wave's amplitude, enhancing the circuit's versatility in various applications.

In practical applications, this triangular wave oscillator circuit can be employed in various electronic systems where precise waveform generation is required, such as in PWM control for motor drives or in signal processing for test equipment. The design's flexibility in adjusting the output voltage range and frequency makes it suitable for a wide range of engineering applications.This application note outlines the implementation of a single-supply, triangular wave oscillator using the MAX9000 and some passive components. The application circuit uses an op amp, comparator, and a voltage reference as active building blocks.

The MAX9000 is chosen because it integrates these three components. The linearity of triangul ar waveforms makes triangular wave generators useful in many "sweep" circuits and test equipment. For example, switched-mode power supplies and induction motor-control circuits often use a triangular wave oscillator as part of the pulse width modulator ( PWM ) circuit. This article presents a compact, triangular wave oscillator using a single MAX9000 IC and some passive components.

The MAX9000 device family integrates a high-speed operational amplifier, a high-speed comparator, and a precision bandgap reference. Figure 1 shows a basic triangular wave generator circuit. It is comprised of two basic building blocks: an integrator to generate the triangular wave output, and a comparator with external hysteresis (Schmitt trigger) to set the amplitude of the triangular wave as desired.

The op amp is configured as an integrator to provide the triangular output. This approach is based on the simple fact that integration of a constant voltage results in a linear ramp. The integrator`s output is fed back to its inverting input by a Schmitt trigger. The input threshold voltages of the Schmitt trigger are designed to change state corresponding to the desired peak voltages of the triangular wave output.

There is a drawback to the circuit in Figure 1: the peaks of the triangular wave can only be symmetrical about the reference voltage applied to the comparator`s inverting input. To generate a triangular wave from 0. 5V to 4. 5V, for example, a reference voltage of (0. 5V + 4. 5V)/2 = 2. 5V is needed. Since a standard bandgap reference has an output voltage of 1. 23V, it would be preferable if the voltage range of the triangular wave could be set independent of the bandgap reference.

This flexibility is achieved by adding resistor R3 to the hysteresis network, as illustrated in Figure 2 where the circuit uses the MAX9000. Resistor R3 enables the peaks of the triangular wave to be set independent of the reference voltage. The input bias current at CIN+ of the comparator is less than 80nA. To minimize errors caused by the input bias current, the current through R2 should be at least 8 µA. Current through R2 is (VREF - VOUT)/R2. Considering the two possible output states to solve for R2, two formulas result: Use the smaller of the two resulting resistor values.

For example, with VDD = 5V, VREF = 1. 23V, and IR2 = 8 µA, the two values of R2 are 471. 25k © and 153. 75k ©. Therefore, for R2 choose the standard value of 154k ©. During the rising ramp of the triangular wave, the comparator`s output is tripped low (VSS). Similarly, the falling ramp requires the comparator`s output to be at logic high (VDD). That is, the comparator must change state corresponding to the required peak and valley points of the triangular wave. Applying nodal analysis at the noninverting input of the comparator and solving for these two thresholds, gives the following simultaneous equations: In this example, the voltage range of the triangular wave is from 0.

5V to 4. 5V. Hence substituting VIH = 4. 5V, VIL = 0. 5V, VDD = 5V, and VREF = 1. 23V yields R1 = 124k © and R3 = 66. 5k ©. The maximum input bias current of the op amp is 2nA. Therefore, to minimize errors the current through R4 must always be greater than 0. 2 µA. This constraint implies that: For this example, choose f = 25kHz, VOUT, P-P = 4V (for a 0. 5V to 4. 5V triangular wave), and VREF = 1. 23V. This gives the time constant as R4 G— C = 9. 27 µs. Select C = 220pF and R4 = 42. 2k ©. The resulting output will match the designed frequency, if the op amp is not slew limited. Since the feedback capacitor ch 🔗 External reference