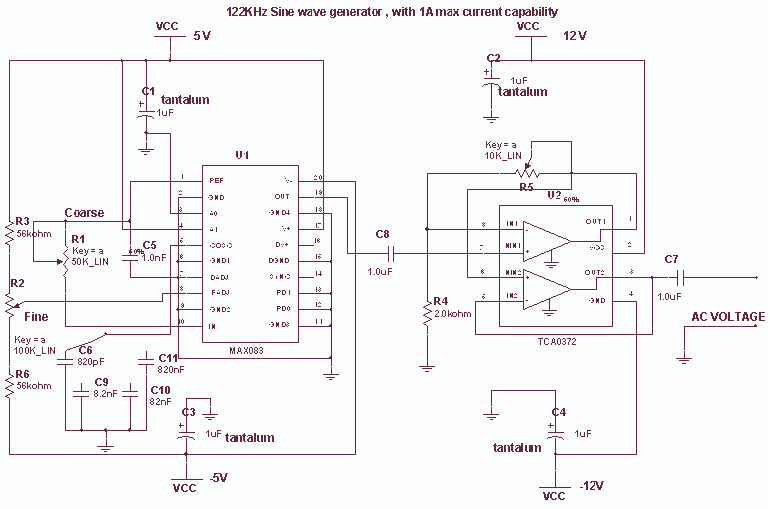
SINE WAVE OSCILLATOR
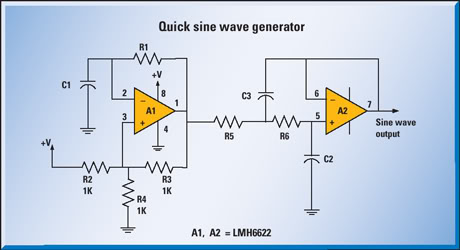
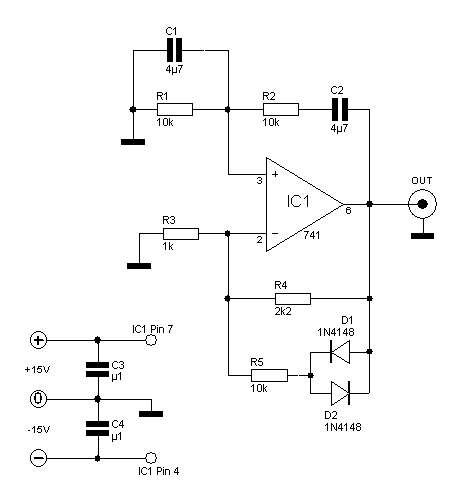
Rf = 100 k preset. The slider is positioned approximately a quarter of the way around. This component is utilized to control the gain, which should be minimized while ensuring the oscillator starts reliably. Zener diodes limit the oscillator output by reducing amplifier gain when the output exceeds their breakdown voltage, although they also compromise the accuracy of the sine wave shape. In the absence of these diodes, the amplifier limits would lead to increased distortion. For a reduced audio output, normal diodes can be substituted in series with the Zener diodes, resulting in an output of around +/- 0.7 volts, suitable for headphones or audio amplifier inputs. This circuit aims for a gain of exactly 1; a lower gain would cause oscillations to decay, while a higher gain would lead to clipping as the op-amp limits the output. If the output is too low, the diodes do not conduct, resulting in increased gain. Conversely, if the output is too high, the diodes conduct, providing negative feedback that reduces gain. The ideal output occurs when the gain is exactly one. Resistors and capacitors (R and C) facilitate positive feedback, reinforcing oscillations at the oscillation frequency while controlling it at other frequencies. Rf provides negative feedback; excessive negative feedback would prevent oscillator startup, while insufficient feedback would lead to output increase until limiting occurs. The following article demonstrates the use of two op-amps to create a simple sine wave generator. It is advised to use a low-speed op-amp instead of a high-speed one, as the latter may introduce oscillation issues. Any standard TTL op-amp will suffice. The output voltage is not critical; adjustments can be made later. Using a 12-volt supply, a sine wave that does not clip can be achieved, whether it results in a peak-to-peak voltage of 10V, 9V, or even 8V. In various design and testing scenarios, a sine wave signal of arbitrary frequency may be required. The subsequent design and accompanying Excel spreadsheet detail a sine wave generator that can be quickly assembled with a dual op-amp and a small number of resistors and capacitors. The schematic for the quick sine wave generator is depicted in Figure 1. This circuit generates a sine wave by first producing a square wave at the desired frequency using amplifier A1, configured as an astable oscillator with frequency determined by R1 and C1. A two-pole low-pass filter using A2 filters the square wave output from A1. This filter is a unity gain Sallen-Key filter with a cutoff frequency equal to the square wave frequency from A1. The square wave consists of the fundamental frequency and its odd harmonics, with the filter removing most harmonic frequencies, leaving the fundamental frequency at the output of A2. The fundamental frequency component of a square wave is approximately 1.27 times the peak amplitude of the square wave, while the sine wave output amplitude will be about 87% of the square wave's peak. The peak of both the square and sine waves will vary with the amplifier's supply voltage and output swing specifications. In this design, frequency is specified alongside the value of C1, and based on these values, R1, C2, C3, R4, and R5 are calculated. The values of R2, R3, and R4 are set to 1 kOhm and should be matched to minimize frequency operation errors.
The described circuit employs a dual op-amp configuration to achieve a sine wave output through a systematic approach of generating a square wave and subsequently filtering it. The astable oscillator configuration of A1 utilizes resistors R1 and capacitors C1 to determine the desired frequency of oscillation, establishing a square wave output. The output of A1 is then processed through the Sallen-Key low-pass filter, which is configured to allow the fundamental frequency of the square wave to pass while attenuating higher harmonics, resulting in a cleaner sine wave output.
The feedback mechanisms in the circuit are crucial for maintaining the desired oscillation characteristics. The gain control via the Rf preset ensures that the system operates at the edge of stability, allowing the oscillator to start reliably without excessive distortion. The use of Zener diodes introduces a level of output limitation that is beneficial in preventing saturation, although at the cost of some waveform fidelity. The substitution of normal diodes for Zener diodes can be employed to tailor the output voltage levels for specific applications, such as interfacing with headphones.
Component selection is based on established formulas that relate frequency, resistance, and capacitance, ensuring that the circuit can be fine-tuned to meet specific performance criteria. The matching of resistor values is also important for maintaining frequency accuracy, as discrepancies can lead to unintended variations in output frequency.
Overall, this sine wave generator circuit is versatile and can be adapted for various applications, including audio signal generation and testing. The straightforward assembly process and reliance on common components make it accessible for rapid prototyping and experimentation in electronic design.Rf = 100 k preset - The slider is set about a quarter of the way round. This is used to control the gain. The gain should be as small as possible consistent with the oscillator starting up reliably. The zener diodes limit the oscillator output by decreasing the amplifier gain if the output rises above their breakdown voltage. They also decrease th e accuracy of the sine wave shape. However if the diodes are not there, the amplifier limits and the distortion is much worse. For a much smaller audio output, replace the Zener diodes in series with normal diodes in parallel. The output will now be about +/- 0. 7 volts, suitable for headphones or the input of an audio amplifier. This circuit is designed to have a gain of exactly 1. If the gain were less, the oscillations would die away. If the gain were more, the pure sine wave would get bigger until the op amp limited and the wave would become clipped. If the output is too small, the diodes don`t conduct. This makes the gain higher. If the output is too large, the diodes to conduct and this negative feedback decreases the gain. When the output is just right, the gain is one. The resistors and capacitors (R and C) provide positive feedback. At the frequency of oscillation, the positive feedback is in phase and this reinforces the oscillations.
At other frequencies, this is not the case so the oscillator frequency is controlled. Rf provides negative feedback. With too much negative feedback, the oscillator would fail to start. With too little feedback, the output would increase until the oscillator limited. The following article will show you how to use two op amps to make a simple sine wave generator. DO NOT USE A HIGH SPEED OP AMP - USE A CHEAP SLOW ONE, TRANSISTOR NOT CMOS. A high speed one would just give you oscillation problems. Any old TTL one you got in the drawer will work just fine. Finally, the output voltage is not critical; we can adjust for that later. Use your 12 volt supply and get a sine that doesn`t clip. If it ends up at P-P 10 v or 9 v or even 8 v it doesn`t matter. In various design and test situations, a sine wave signal with an arbitrary frequency may be needed. The following design, and accompanying Excel spreadsheet implement a sine wave generator that can be quickly assembled with a dual op amp and small number of resistors and capacitors. Figure 1 shows the schematic for the quick sine wave generator: This circuit generates a sine wave by first generating a square wave, at the required frequency, with amplifier A1 that is configured as an astable oscillator with the frequency determined by R1 and C1.
The two-pole low pass filter, using A2, filters the square wave output from A1. The filter is a unity gain Sallen-Keys filter with its cut off frequency equal to the square wave frequency from A1. The square wave is made up of the fundamental frequency and the odd harmonics of the fundamental frequency.
The filter removes most of the harmonic frequencies and the fundamental frequency remains at the output of A2. The fundamental frequency component of a square wave is about 1. 27 times the peak amplitude of the square wave and the amplitude of the sine wave output will be approximately 87 percent of the peak of the square wave.
The peak of the square wave will depend on the amplifier`s supply voltage and the output swing specification of the amplifier. Additionally, the peak of the square and the sine wave will track changes in the amplifier`s supply voltage.
In this design, the frequency is specified along with the value of C1 and based on these values, the values of R1, C2, C3, R4, and R5 are calculated. The values of R2, R3 and R4 are 1K Ohms and should be matched in value to help minimize errors in the actual frequency of operation compared to the calculated frequency of operation.
The equations for the component selection follow. The frequency, F, is the required sine wave frequency. The value f 🔗 External reference
The described circuit employs a dual op-amp configuration to achieve a sine wave output through a systematic approach of generating a square wave and subsequently filtering it. The astable oscillator configuration of A1 utilizes resistors R1 and capacitors C1 to determine the desired frequency of oscillation, establishing a square wave output. The output of A1 is then processed through the Sallen-Key low-pass filter, which is configured to allow the fundamental frequency of the square wave to pass while attenuating higher harmonics, resulting in a cleaner sine wave output.
The feedback mechanisms in the circuit are crucial for maintaining the desired oscillation characteristics. The gain control via the Rf preset ensures that the system operates at the edge of stability, allowing the oscillator to start reliably without excessive distortion. The use of Zener diodes introduces a level of output limitation that is beneficial in preventing saturation, although at the cost of some waveform fidelity. The substitution of normal diodes for Zener diodes can be employed to tailor the output voltage levels for specific applications, such as interfacing with headphones.
Component selection is based on established formulas that relate frequency, resistance, and capacitance, ensuring that the circuit can be fine-tuned to meet specific performance criteria. The matching of resistor values is also important for maintaining frequency accuracy, as discrepancies can lead to unintended variations in output frequency.
Overall, this sine wave generator circuit is versatile and can be adapted for various applications, including audio signal generation and testing. The straightforward assembly process and reliance on common components make it accessible for rapid prototyping and experimentation in electronic design.Rf = 100 k preset - The slider is set about a quarter of the way round. This is used to control the gain. The gain should be as small as possible consistent with the oscillator starting up reliably. The zener diodes limit the oscillator output by decreasing the amplifier gain if the output rises above their breakdown voltage. They also decrease th e accuracy of the sine wave shape. However if the diodes are not there, the amplifier limits and the distortion is much worse. For a much smaller audio output, replace the Zener diodes in series with normal diodes in parallel. The output will now be about +/- 0. 7 volts, suitable for headphones or the input of an audio amplifier. This circuit is designed to have a gain of exactly 1. If the gain were less, the oscillations would die away. If the gain were more, the pure sine wave would get bigger until the op amp limited and the wave would become clipped. If the output is too small, the diodes don`t conduct. This makes the gain higher. If the output is too large, the diodes to conduct and this negative feedback decreases the gain. When the output is just right, the gain is one. The resistors and capacitors (R and C) provide positive feedback. At the frequency of oscillation, the positive feedback is in phase and this reinforces the oscillations.
At other frequencies, this is not the case so the oscillator frequency is controlled. Rf provides negative feedback. With too much negative feedback, the oscillator would fail to start. With too little feedback, the output would increase until the oscillator limited. The following article will show you how to use two op amps to make a simple sine wave generator. DO NOT USE A HIGH SPEED OP AMP - USE A CHEAP SLOW ONE, TRANSISTOR NOT CMOS. A high speed one would just give you oscillation problems. Any old TTL one you got in the drawer will work just fine. Finally, the output voltage is not critical; we can adjust for that later. Use your 12 volt supply and get a sine that doesn`t clip. If it ends up at P-P 10 v or 9 v or even 8 v it doesn`t matter. In various design and test situations, a sine wave signal with an arbitrary frequency may be needed. The following design, and accompanying Excel spreadsheet implement a sine wave generator that can be quickly assembled with a dual op amp and small number of resistors and capacitors. Figure 1 shows the schematic for the quick sine wave generator: This circuit generates a sine wave by first generating a square wave, at the required frequency, with amplifier A1 that is configured as an astable oscillator with the frequency determined by R1 and C1.
The two-pole low pass filter, using A2, filters the square wave output from A1. The filter is a unity gain Sallen-Keys filter with its cut off frequency equal to the square wave frequency from A1. The square wave is made up of the fundamental frequency and the odd harmonics of the fundamental frequency.
The filter removes most of the harmonic frequencies and the fundamental frequency remains at the output of A2. The fundamental frequency component of a square wave is about 1. 27 times the peak amplitude of the square wave and the amplitude of the sine wave output will be approximately 87 percent of the peak of the square wave.
The peak of the square wave will depend on the amplifier`s supply voltage and the output swing specification of the amplifier. Additionally, the peak of the square and the sine wave will track changes in the amplifier`s supply voltage.
In this design, the frequency is specified along with the value of C1 and based on these values, the values of R1, C2, C3, R4, and R5 are calculated. The values of R2, R3 and R4 are 1K Ohms and should be matched in value to help minimize errors in the actual frequency of operation compared to the calculated frequency of operation.
The equations for the component selection follow. The frequency, F, is the required sine wave frequency. The value f 🔗 External reference
Related Circuits
In DA3, DA5, VT1, and VT2, the first channel of the VLF Class D amplifier is assembled. The second channel is constructed using DA4, DA7, VT3, and VT4. Antiphase sine waves in the VLF range are formed at the...
An operational amplifier (op amp) configured as a comparator generates a 10-V peak-to-peak square wave output with a 100-mV input signal at a frequency of up to 15 kHz. The resistor R5 can be adjusted to achieve symmetry in...
This is a Voltage Controlled Oscillator (VCO) circuit. This circuit is based on a Hartley oscillator. The frequency depends on the values of C1 and L1. The Voltage Controlled Oscillator (VCO) circuit described operates using a Hartley oscillator configuration, which...
This circuit utilizes an adjustable resonant tank circuit that ensures operation at the desired crystal overtone. Capacitor C1 and inductor L1 form the resonant tank circuit, which can be adjusted to achieve a resonant frequency ranging from approximately 50...
Transistor RC phase shift oscillator. RC phase shift oscillator using operational amplifier. RC phase shift network. Theory and working principle. Circuit diagram. The transistor RC phase shift oscillator is a type of electronic oscillator that generates sine wave signals. This...
This is a quartz-stabilized oscillator circuit with electronic gain control. Replacing the common filament lamp for amplitude stabilization, this circuit uses... This circuit represents a quartz-stabilized oscillator featuring electronic gain control, which enhances the stability and precision of the output...