1MHz PIERCE OSCILLATORS

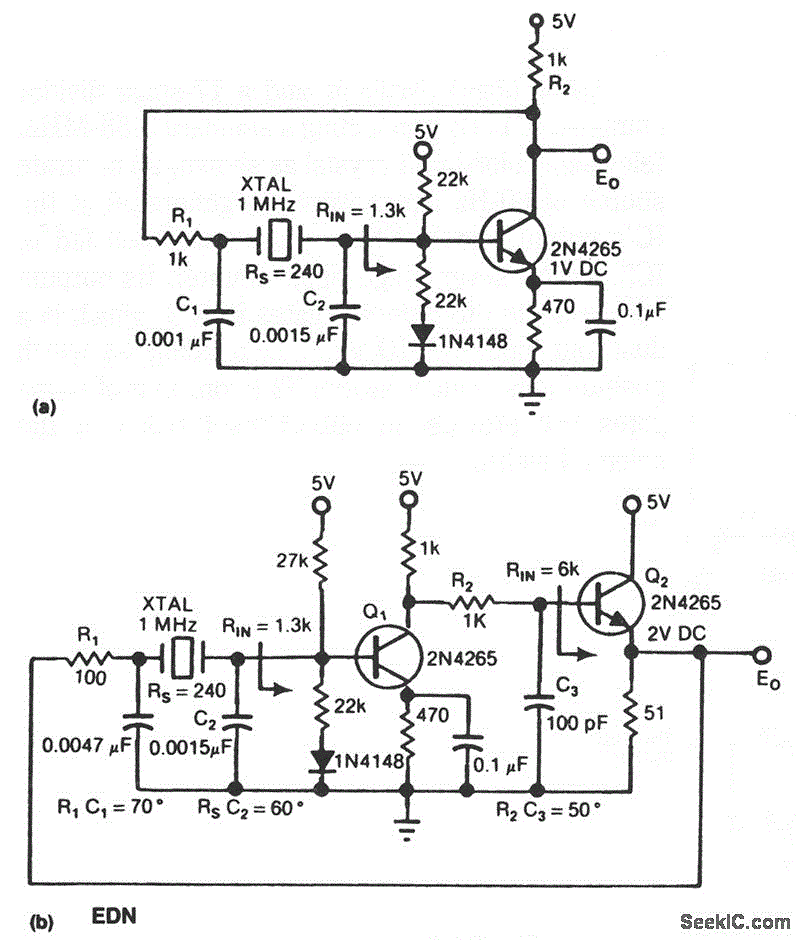
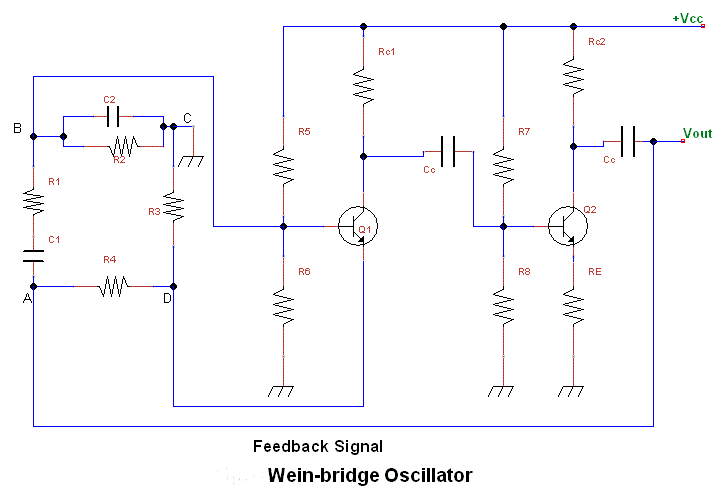
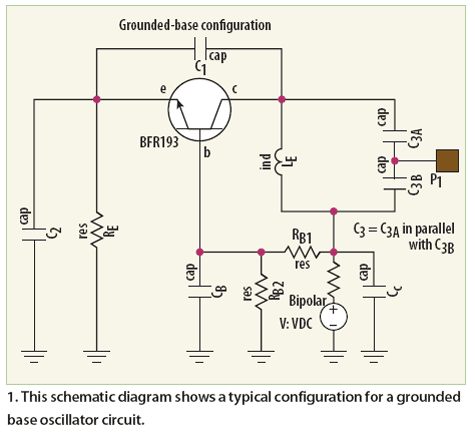
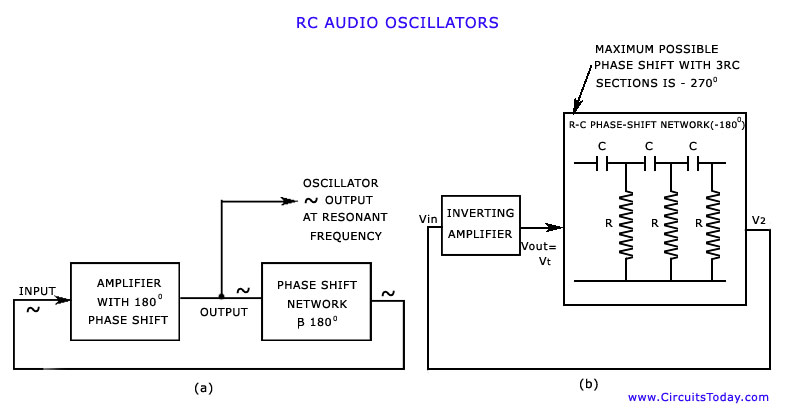
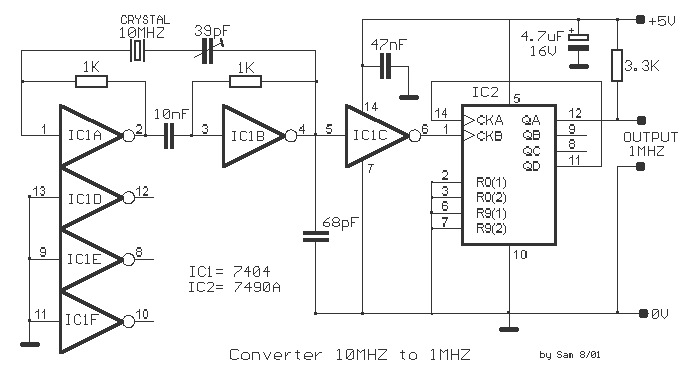
A simple network design is a key feature of the Pierce circuit, as illustrated by these 1-MHz oscillators. Operating the crystal slightly above resonance requires only one high-gain transistor stage. Operating it exactly at series resonance requires an additional RC phase lag and two transistors, which can have lower gain.

The Pierce oscillator is a type of crystal oscillator that utilizes a feedback loop to generate oscillations. It typically consists of a crystal, a transistor (or a combination of transistors), and passive components such as resistors and capacitors. The unique aspect of the Pierce circuit is its ability to operate efficiently at various frequencies, particularly around 1 MHz in this context.

When the crystal is operated slightly above its resonant frequency, the circuit can achieve stable oscillation with minimal complexity, requiring only a single high-gain transistor. This configuration is advantageous for applications where simplicity and space-saving are paramount. The high-gain transistor amplifies the signal, ensuring that the oscillation continues without the need for additional components.

Conversely, when the crystal is operated at its exact series resonance, the configuration demands an additional RC phase lag network and a second transistor. This adjustment is necessary to maintain the phase condition required for sustained oscillation, as the feedback loop must provide a total phase shift of 360 degrees (or 0 degrees) to ensure that the output is in phase with the input. The introduction of a second transistor allows for lower gain transistors to be used, which can be beneficial in applications where power consumption is a concern.

The choice of using a single or dual transistor configuration ultimately depends on the specific requirements of the application, including frequency stability, power consumption, and circuit complexity. The Pierce circuit's versatility makes it suitable for a wide range of applications in frequency generation, timing circuits, and signal processing, where precise frequency control is essential.Simple network design is a key feature of the Pierce circuit, as these 1-MHz oscillators illustrate.Operating the crystal slightly above resonance (Fig.21-5a) requires only one high-gain transistor stage.Operating it exactly at series resonance (Fig. 21-5b) requires an extra RC phase lag and two transistors which can have lower gain.. 🔗 External reference