Oscillator operation-working-feedback circuit block diagram

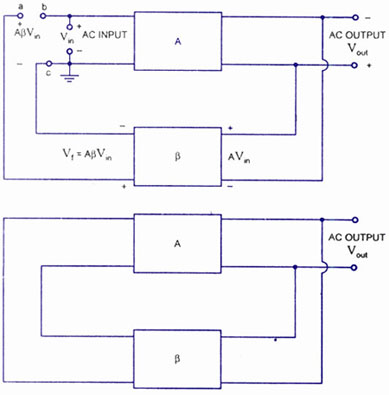
A feedback amplifier with a closed-loop gain, Af, greater than unity can be achieved through the use of positive feedback. This condition also fulfills the phase requirement, leading to the operation of an oscillator circuit. An oscillator circuit generates a continuously varying output signal. If the output signal varies sinusoidally, it is referred to as a sinusoidal oscillator. Conversely, if the output voltage rapidly alternates between different voltage levels, it is termed a pulse or square-wave generator. To understand how an oscillator produces an output signal without an external input, consider the feedback circuit. In this configuration, Vin is the AC input voltage driving the input terminals B-C of an amplifier with a voltage gain A. This voltage feeds into a feedback circuit, typically a resonant circuit, which provides maximum feedback at a specific frequency. The feedback voltage returning to point a is expressed as Vf = A²Vin, where ² represents the gain of the feedback network. If the phase shift through the amplifier and feedback circuit is zero, then A²Vin is in phase with the input signal Vin at the amplifier's input terminals. When point a is connected to point b and the voltage source Vin is removed, the feedback voltage A²Vin drives the input terminals B-C of the amplifier. If A² is less than unity, A²Vin is smaller than Vin, causing the output signal to diminish. Conversely, if A² is greater than unity, the output signal will amplify. When A² equals unity, A²Vin equals Vin, resulting in a steady sine wave output. In this scenario, the circuit generates its own input signal, producing a sinusoidal output without the need for an external input to initiate oscillations. To achieve self-sustained oscillation, the condition A² = 1 must be satisfied, and the value of A² is adjusted to be greater than unity. Consequently, the system begins oscillating by amplifying the inherent noise voltage present. A practical average value of A² equal to 1 can be attained through saturation factors in real circuits, although the resulting waveforms may not be perfectly sinusoidal. As the value of A² approaches 1, the waveform becomes increasingly sinusoidal. The feedback circuit's design ensures that the phase shift around the loop is 0° at the resonant frequency, with deviations from 0° occurring above and below this frequency. Thus, oscillations will only manifest at the resonant frequency of the feedback circuit.

The feedback amplifier operates on the principle of positive feedback, which is essential for generating sustained oscillations. The closed-loop gain, Af, must exceed unity to ensure that the oscillations can build upon themselves. The positive feedback mechanism allows the amplifier to utilize its own output to drive the input, creating a self-sustaining loop. The resonant feedback circuit plays a crucial role in determining the frequency of oscillation, as it is designed to provide maximum feedback at a specific frequency.

In practical applications, the circuit is often implemented using components such as operational amplifiers, resistors, capacitors, and inductors to form the necessary feedback network. The choice of these components influences the stability and frequency of the oscillation. For instance, the resonant frequency can be calculated based on the values of the inductance and capacitance in the feedback loop, ensuring that the desired frequency of oscillation is achieved.

The behavior of the circuit can be further analyzed through Bode plots or frequency response analysis, which illustrate how the gain and phase shift vary with frequency. This analysis is critical for designing circuits that require precise oscillation characteristics, such as in signal generators, clock circuits, and RF transmitters.

Overall, the feedback amplifier and its associated feedback network are integral to the operation of oscillators, providing a means to generate consistent, repeatable signals without reliance on an external input. The careful design and tuning of the feedback components allow for a wide range of applications in electronic systems.A feedback amplifier having closed-loop gain, Af greater than unity can be obtained by the use of a positive feedback. This result also satisfies the phase condition and thus results in the operation of an oscillator circuit.

An oscillator circuit then provides a constantly varying output signal. If the out ­put signal varies sinusoidally, the cir cuit can be called as a sinusoidal oscillator. But, if the output voltage rises and drops from one voltage level to another quickly, the circuit can be called a pulse or square-wave genera ­tor. To understand how an oscil ­lator produces an output signal without an external input signal, let us consider the feedback circuit shown in fig (a).

In the figure Vin is the voltage of ac input driving the input terminals B-C of an amplifier having voltage gain A. This voltage drives a feedback circuit that is usually a resonant circuit, as we get maximum feedback at one frequency.

The feedback voltage returning to point a is given by equationVf = A ² Vin where ² is the gain of feedback network If the phase shift through the amplifier and feedback circuit is zero, then A ² Vin is in phase with the input signal Vin that drives the input terminals of the amplifier. Now we connect point a` to point b` and simultaneously remove voltage source Vin, then feedback voltage A ² Vin drives the input terminals b c of the amplifier, as shown in fig.

(b). In case A ² is less than unity, A ² Vin is less than Vin and the output signal will die out, as illustrated in second fig. (a). On the other hand if A P is greater than unity, the output signal will build up, as illustrated in second fig.

(b). If A ² is equal to unity, A ² Vin equals Vin and the output signal is a steady sine wave, as illustrated in fig. (c). In this case the circuit supplies its own input signal and produces a sinusoidal output. There is no need of an input signal for the initiation of oscillations. In order to obtain a self-sustained oscillation, the condition ² A = 1 must be satisfied. The value of ² A is made greater than unity. As a result the system starts oscillating by amplifying noise voltage which is always present. An average value of ² A of 1 can be obtained by the saturation factors in the practical circuits. The waveforms that are obtained will not be exactly sinusoidal. If the value of ² A is closer to the value 1, the waveform becomes more sinusoidal. The figure above shows how the noise voltage resultsin a build up of a steady state oscillation condition.

The gain with feedback, Af becomes infinite as the denominator becomes zero. Thus, a measurable output voltage can be obtained with the help of an infinite signal (noise voltage), and the circuit acts as an oscillator even without an input signal. At the resonant frequency, the phase shift around the loop is made 0 ° by deliberate design. The phase shift is different from 0 ° above and below the resonant frequency. Thus, the resonant frequency of the feedback circuit will be the only frequency where the oscillations will be obtained.

🔗 External reference