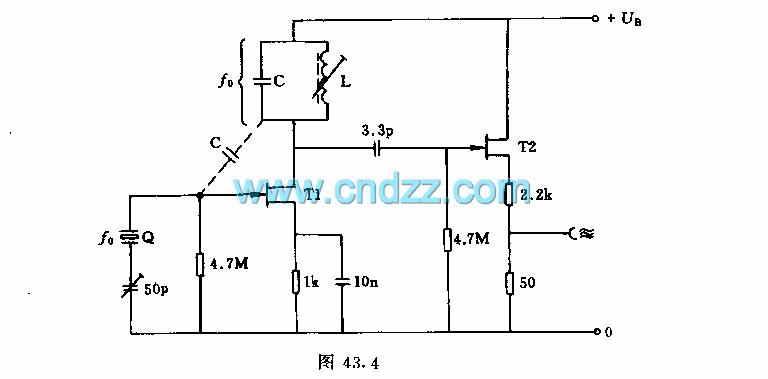
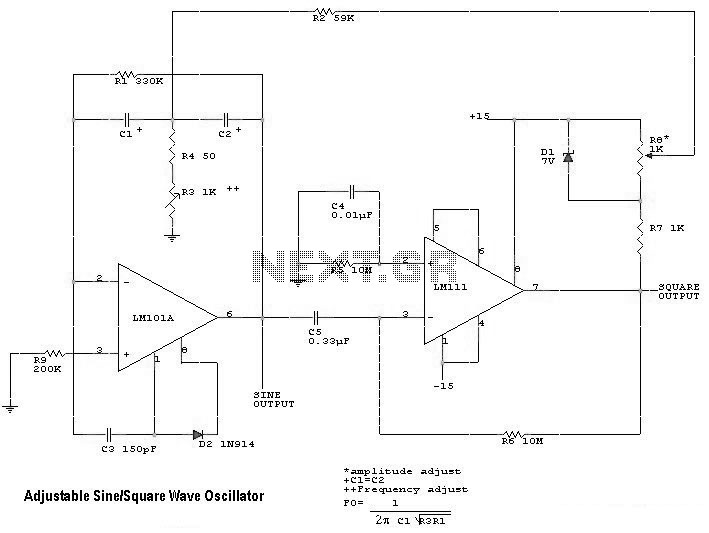
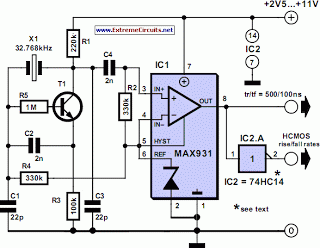
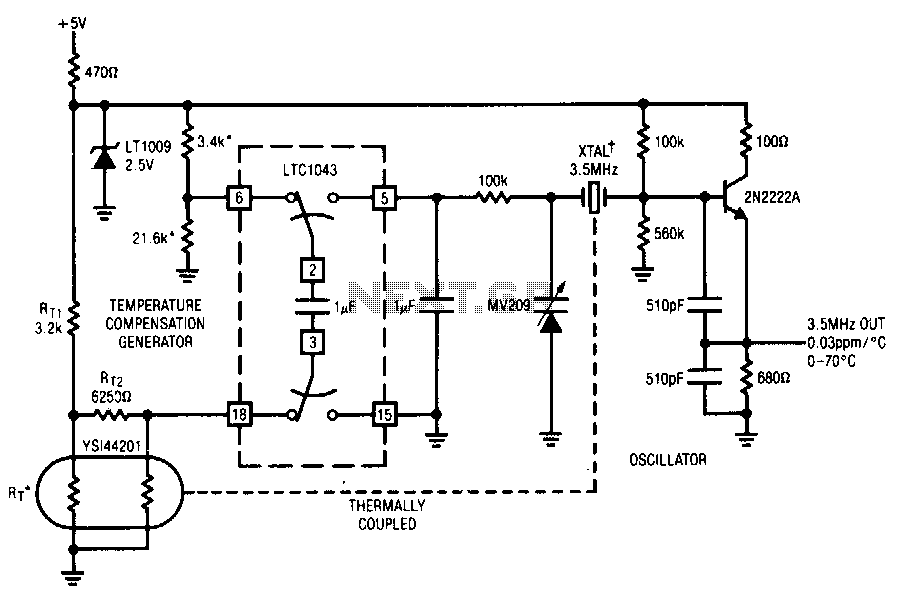
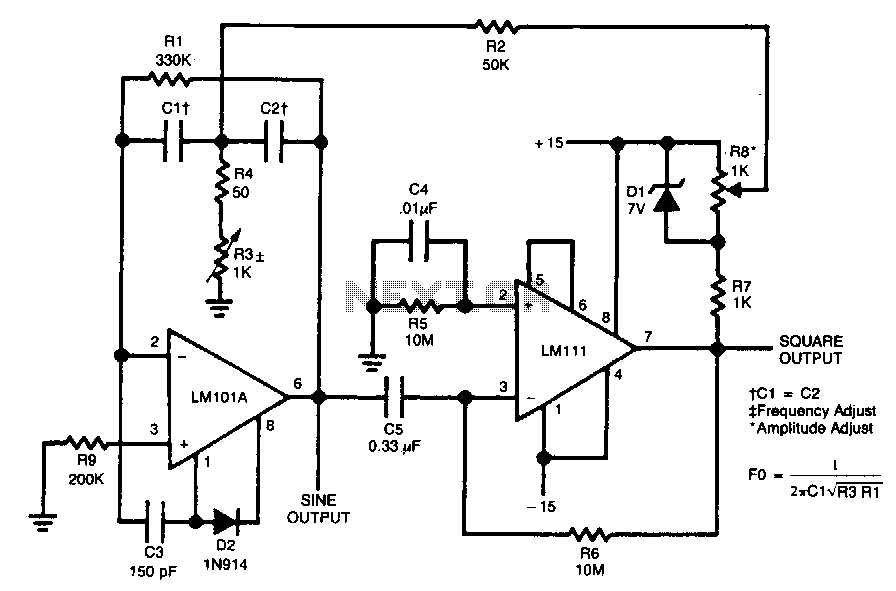
Three-point oscillator inductor

A three-point oscillator, also known as a Hartley oscillator, is similar to the Colpitts oscillator; however, its feedback circuit consists of two series inductors and a capacitor.

The three-point oscillator is a type of electronic oscillator that generates sine waves. It utilizes a feedback loop to maintain oscillation, with its fundamental operation based on the principles of resonance. The Hartley oscillator specifically employs two inductors connected in series, which are tapped to create the feedback necessary for oscillation. This configuration allows for a wide range of frequency tuning by adjusting the values of the inductors or the capacitor in the circuit.

In contrast to the Colpitts oscillator, which uses a capacitive feedback network, the Hartley oscillator's reliance on inductors can yield different performance characteristics, such as stability and frequency range. The series inductors are typically wound on a common core, which helps in minimizing the size of the circuit while maximizing the inductance.

The oscillator's frequency of operation is determined by the formula:

\[ f = \frac{1}{2\pi \sqrt{L_{total} \cdot C}} \]

where \( L_{total} \) is the equivalent inductance of the two inductors and \( C \) is the capacitance of the capacitor in the feedback loop. The total inductance can be calculated based on the individual inductances of the inductors and their coupling factor.

In practical applications, the Hartley oscillator is widely used in radio frequency (RF) applications due to its simplicity and effectiveness in generating high-frequency signals. It is often implemented in RF transmitters and receivers, where precise frequency control is necessary. Additionally, the design can be adapted to include variable inductors or capacitors to allow for fine-tuning of the output frequency.

The circuit typically consists of an active device such as a transistor or an operational amplifier, which provides the necessary gain to sustain oscillations. Proper biasing of the active device is crucial to ensure stable operation and to prevent distortion of the output waveform.

Overall, the Hartley oscillator remains a fundamental circuit in electronics, demonstrating the principles of oscillation and resonance in a straightforward and effective manner.A sense of three-point oscillator, also known as Hartley oscillator, the Colpitts oscillator with similar, but the feedback circuit is composed of two series inductor and a shu nt capacitor composed of