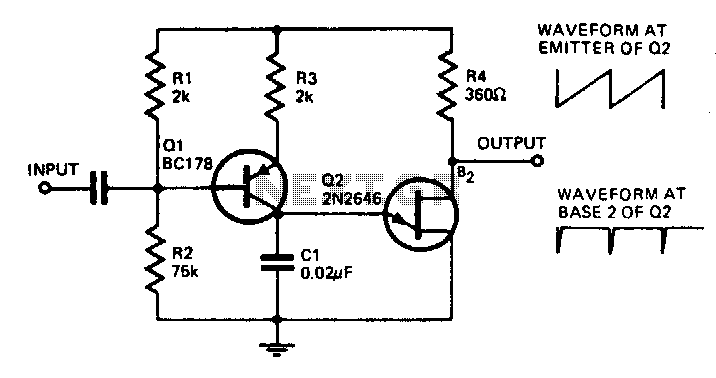
Colpitts Oscillator Calculator

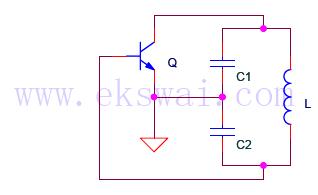
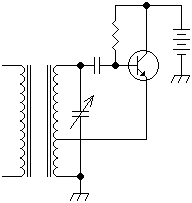
The Colpitts oscillator circuit is illustrated in Figure 1, with Q representing the transistor. The Colpitts and Hartley oscillator circuits are similar, differing primarily in the positions of the inductor and capacitor. An equivalent circuit of the oscillator is depicted in Figure 2. Capacitors C1, C2, and inductor L create a positive feedback network at a selected frequency, with feedback signals originating from both ends of capacitor C2, making it a three-point capacitor oscillator circuit, also referred to as a feedback capacitor oscillator circuit. The feedback signal is in phase with the input voltage, satisfying the oscillation phase equilibrium conditions. The Q value of the LC resonant circuit must be sufficiently high, allowing the circuit's oscillation frequency to approximate the resonant frequency. This can be calculated as follows: The three-point oscillator circuit is characterized by a high oscillation frequency, often exceeding 100 MHz. Due to the low harmonic impedance of C2, the feedback voltage in the higher harmonic components is reduced, resulting in improved oscillation waveforms. Additionally, at high oscillation frequencies, the values of C1 and C2 are very small, leading to significant impacts from transistor-level capacitance on the frequency.

The Colpitts oscillator is a type of electronic oscillator that generates sinusoidal waveforms through the use of a transistor and a combination of capacitors and inductors. The configuration is distinguished by its ability to provide stable oscillations at high frequencies, making it suitable for applications in RF (radio frequency) communication and signal generation.

In this circuit, the transistor Q acts as an amplifier, providing the necessary gain for the oscillator to function. The capacitors C1 and C2, along with the inductor L, form a resonant tank circuit that determines the frequency of oscillation. The feedback network is crucial for sustaining oscillations; it ensures that a portion of the output signal is fed back to the input in phase with the original signal. This phase alignment is essential for maintaining continuous oscillation.

The formula for the resonant frequency (f) of the Colpitts oscillator can be expressed as:

\[
f = \frac{1}{2\pi\sqrt{L \cdot C_{eq}}}
\]

where \( C_{eq} \) is the equivalent capacitance of the capacitors C1 and C2, calculated using the formula for capacitors in series:

\[
\frac{1}{C_{eq}} = \frac{1}{C1} + \frac{1}{C2}
\]

The high Q value of the LC circuit is critical as it indicates low energy loss relative to the energy stored in the circuit, allowing for stable oscillations. The design must take into account the parasitic capacitances associated with the transistor, especially at higher frequencies, as these can significantly affect performance.

In high-frequency applications, the values of C1 and C2 are typically in the picofarad range, which minimizes their impact on the oscillation frequency while ensuring that the circuit can achieve the desired operational characteristics. The careful selection of components is necessary to optimize performance, particularly in achieving a clean oscillation waveform and maintaining frequency stability under varying load conditions.

Overall, the Colpitts oscillator circuit is a versatile and widely used design in electronic engineering, particularly in applications requiring precise frequency generation and signal processing.Colpitts oscillator circuit is shown in Figure 1, Q is the transistor. The Colpitts and Hartley oscillator circuit are similar, except the inductor, capacitor exchange of positions. Oscillator equivalent circuit shown in Figure 2. Capacitors C1, C2, and inductor L form a positive feedback network of selected frequency, feedback signals from both e

nds of capacitor C2, so called three-points capacitor oscillator circuit, also known as the feedback capacitor oscillator circuit. Feedback signal in phase with the input voltage to meet the oscillation of the phase equilibrium conditions, LC resonant circuit Q value is high enough under the conditions of the circuit`s oscillation frequency is approximately equal to the resonant frequency circuit.

Calculated as follows: Capacitance three-point oscillator circuit is characterized by a high oscillation frequency can do in general can reach more than 100MHz, because of the high harmonic impedance of C2 is small, the feedback voltage in the high harmonic components smaller, and thus oscillation waveform better. Also when the oscillation frequency is high, C1, C2`s value is very small, transistor-level capacitance will impact on the frequency.

🔗 External reference