digital logic How to calculate Gate Delays in normal Adders and Carry Look Ahead Adders

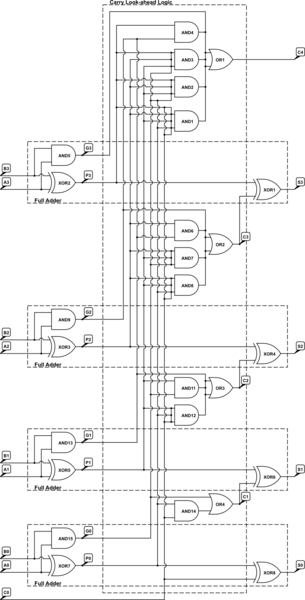
A 4-bit Carry Look Ahead Adder has 3 gate delays for all carry bits and 4 gate delays for all sum bits, whereas ripple adders have 7 and 8 gate delays, respectively.

The 4-bit Carry Look Ahead Adder (CLA) is designed to improve the speed of binary addition by reducing the time required to calculate carry bits compared to traditional ripple carry adders. In a ripple carry adder, each carry bit must wait for the previous carry bit to be calculated, resulting in a cumulative delay that can significantly impact performance, especially in larger bit-width adders.

The CLA utilizes a more sophisticated approach by employing generate (G) and propagate (P) signals to determine the carry bits in parallel. The generate signal indicates whether a carry will be produced from a given bit position, while the propagate signal indicates whether a carry will be propagated to the next bit. The carry-out for each bit can be computed using the equations:

- C1 = G0 + P0 * C0
- C2 = G1 + P1 * C1
- C3 = G2 + P2 * C2
- C4 = G3 + P3 * C3

This allows for the simultaneous calculation of carry bits, which is the reason for the reduced gate delay of 3 for carry bits in a 4-bit CLA. The sum bits are calculated using the carry signals and the input bits, leading to a total of 4 gate delays for the sums.

In contrast, a ripple carry adder experiences a sequential delay, where each carry must be computed before proceeding to the next, resulting in longer delays of 7 and 8 gate delays for carry and sum bits, respectively. The efficiency of the CLA makes it ideal for high-speed arithmetic operations in digital circuits.For a 4-bit Carry Look Ahead Adder have 3 gate delays for all carry bits and 4 gate delays for all sum bits, while it is stated as 7 and 8 in case of ripple adders. How, was this calculated The image of 4 bit carry look ahead adder is shown below: 🔗 External reference