Fast Binary Adding Circuits

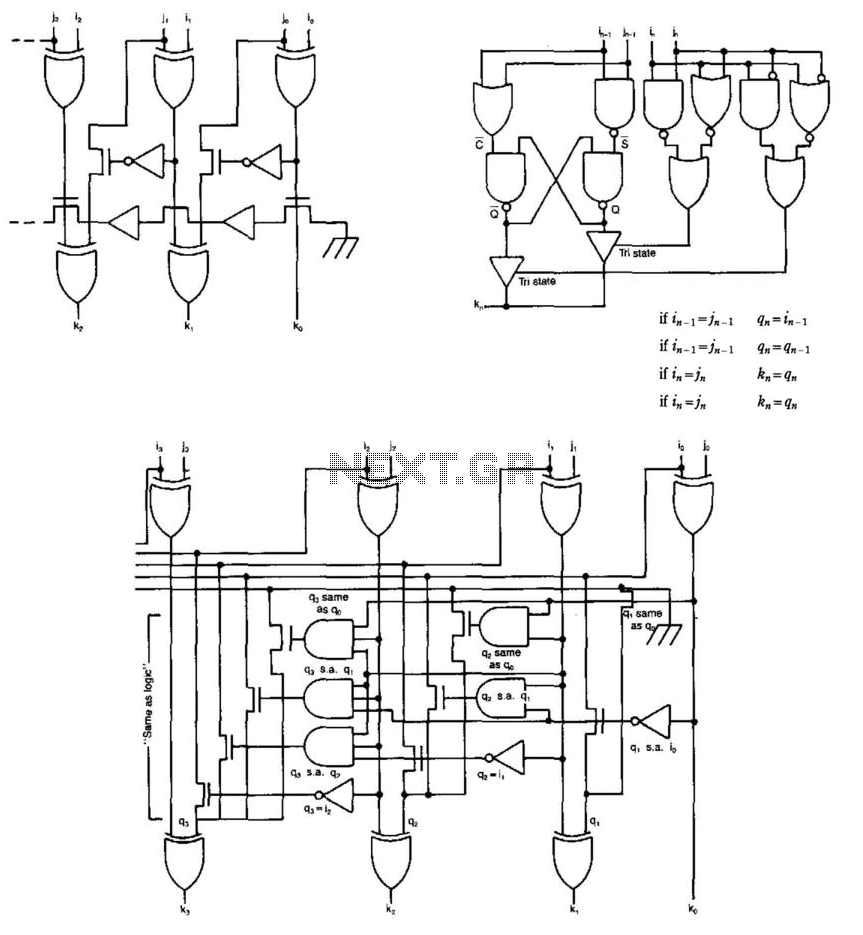
Some circuits that add binary numbers experience time delays due to carry propagation. This issue has been partially addressed by the carry look-ahead adder. However, the complexity of this method typically limits its application to no more than 4 bits, necessitating a ripple carry between the carry look-ahead blocks. The Daniels Adder circumvents these issues by employing a scheme that eliminates the use of carry bits during binary addition. It relies on recognition patterns derived from the binary addition truth table. The addition process is defined by two sets of equations, with the boundary condition that q_i = 0, where in, j, and k represent the bits of binary weight 2^n (the nth bit) of the addend, summand, and sum, respectively. The variable qn serves as an intermediate variable, and qn is the inverse of qn. The sum's value, depending on in and j, is either the same as or the inverse of the (n-1)th bit of the sum. Figure 45-1 (a) illustrates the logic diagram of the ripple-through implementation of the adder. Each stage computes whether its intermediate variable qn matches the previous stage's value (g_i) in parallel, allowing for the development of simple "same as" logic that avoids the complexity of carry look-ahead logic and can be extended across any number of bits (Fig. 45-1 (b)). A 32-bit adder designed in this manner results in 11-gate delays, with no gate having more than 4 inputs. The pipelined implementation (Fig. 45-1 (c)) is particularly compact and efficient, enabling the production of the sum at a rate of 3-gate delays per bit. These high-speed adder circuits are suitable for gate arrays or full-custom integrated circuits (ICs) to facilitate rapid calculations of addresses or data values. Their compact design also minimizes silicon space usage compared to conventional adders.

The Daniels Adder presents a significant advancement in digital circuit design, particularly in binary addition processes. By eliminating carry bits, it simplifies the addition operation, allowing for more efficient circuit implementations. The reliance on recognition patterns enhances the speed and reliability of the addition process, as it aligns closely with the fundamental principles of binary arithmetic.

The logic diagram in Figure 45-1 (a) showcases the ripple-through implementation, where each stage operates independently yet simultaneously. This parallel processing capability is critical in achieving high-speed performance. The intermediate variable qn acts as a critical component in determining the output of each stage, allowing the circuit to quickly ascertain whether the current addition operation aligns with the previous stage's result.

In terms of scalability, the architecture of the Daniels Adder supports expansion beyond 4 bits without the complications introduced by traditional carry look-ahead adders. This characteristic is particularly advantageous in applications requiring large-scale binary addition, such as in digital signal processing or high-performance computing environments.

The pipelined design, as depicted in Figure 45-1 (c), further enhances the performance of the adder by allowing multiple addition operations to occur simultaneously across different pipeline stages. This design not only reduces the overall time required to compute the sum but also maximizes the utilization of available circuit resources.

In conclusion, the Daniels Adder represents a modern solution to the challenges posed by carry propagation in binary addition. Its innovative approach to circuit design not only improves speed and efficiency but also reduces silicon area, making it a valuable addition to the toolkit of electronic engineers engaged in the design of high-performance digital systems. Some circuits that add binary numbers have problems with time delay caused by carry propagation. This has been partially solved by the carry look-ahead adder. However, because of the complexity of this scheme, the carry look-ahead logic usually covers no more than 4 bits, and a ripple carry is implemented between the carry look-ahead blocks. The Daniels Adder avoids these problems by presenting a scheme where carry bits are not used at all in the process of binary addition.

It is based on recognition patterns, which exist with the binary addition truth table. The addition is described by the following two sets of equations: with the boundary condition that q_i = 0, where in, j„, and k)t are the bit of binary weight 2n (nth bit) of the addend, summand, and sum respectively, qn is an intermediate variable and qn is the inverse oiqn. The value of the sum is (depending upon in and ;„) either the same as or the inverse of (depending upon ift- and aO, al, or the inverse of the («-l)th bit of the sum.

Figure 45-1 (a) shows the logic diagram of the ripple through implementation of the adder. Because each stage calculates whether its value of the intermediate variable q„ is the same as the previous stage"s value (g„_i) in parallel, it is possible to devise simple "same as" logic that does not have the complexity drawback of carry look-ahead logic and can be carried over any number of bits (Fig. 45-1 (b)). A 32-bit adder built in this way will result in 11-gate delays (no gate having more than 4 inputs). Especially compact and efficient is the pipelined implementation (Fig. 45-1 (c)), which can produce the sum at a rate of 3-gate delays/bit. The high-speed adder circuits can be used on gate arrays or full-custom ICs to implement fast calculation of addresses or data values.

Because of their compact nature, they also use less space on the silicon than conventional adders do. 🔗 External reference