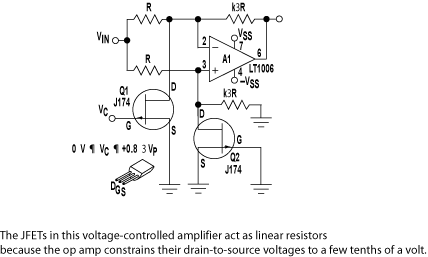
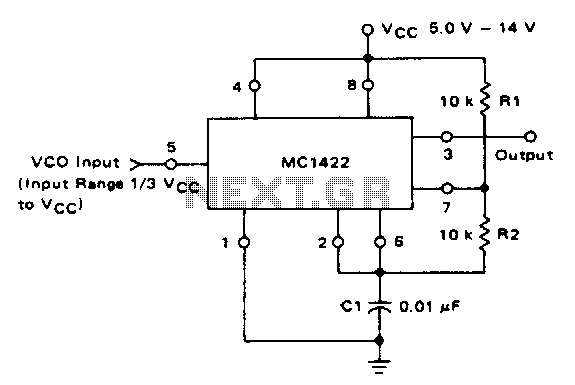
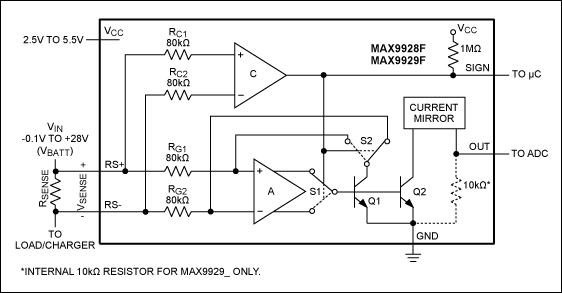
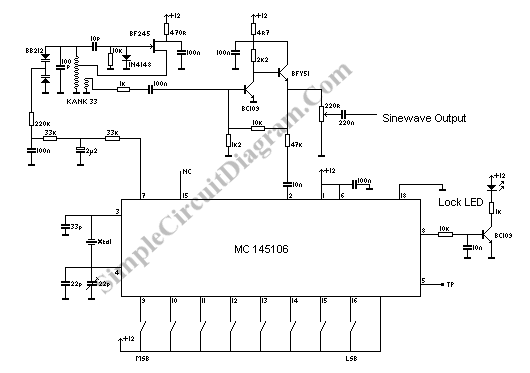
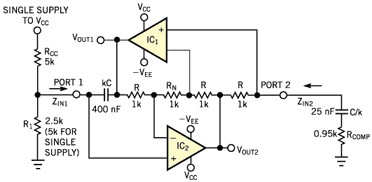
RF OSCILLATOR CIRCUITS

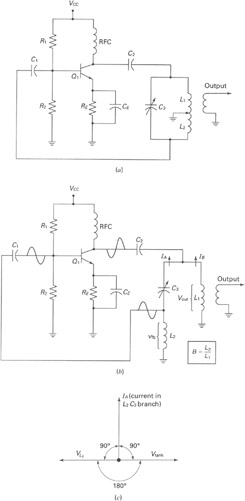
A widely recognized circuit is the Hartley oscillator, which is characterized by a tapped coil within the LC tank circuit. The tap point of the coil is grounded. The oscillator's amplifier section functions as a common-emitter amplifier, resulting in the AC base voltage and AC collector voltage being 180 degrees out of phase. Consequently, the feedback network must introduce an additional 180-degree phase shift to ensure that the feedback voltage has the correct phase for sustaining oscillations. For a clearer understanding of the circuit's operation, it has been illustrated in Figure 2-2(b). It is important to note that L1 is in parallel with L2, while C3 is in series. At the resonant frequency of the tank circuit, the net reactance of the L2-C3 branch behaves in a capacitive manner. Furthermore, the net capacitive reactance of the L2-C3 branch is equal to the inductive reactance of the L1 branch, leading to a specific mathematical relationship.

The Hartley oscillator is a type of LC oscillator that utilizes an inductor-capacitor (LC) tank circuit to generate oscillations. The key component of this circuit is the tapped inductor, which allows for the division of inductance into two parts, L1 and L2. The configuration of the inductor and capacitor determines the frequency of oscillation. The oscillator operates based on the principle of positive feedback, where a portion of the output is fed back to the input to sustain the oscillations.

In this configuration, the common-emitter amplifier plays a crucial role in amplifying the signal. The grounding of the tap point in the inductor ensures that the phase relationship between the input and output signals is maintained correctly. The requirement for the feedback network to provide an additional 180-degree phase shift is essential for the system to oscillate, as it ensures that the feedback voltage reinforces the input signal.

The resonant frequency of the tank circuit is determined by the values of L1, L2, and C3. At this frequency, the reactance of the capacitive branch (L2-C3) effectively cancels out the inductive reactance of L1, resulting in a condition where the circuit can sustain oscillations. This balance between inductive and capacitive reactance is critical for the stability and performance of the oscillator.

Mathematically, the relationship governing the oscillation frequency can be expressed as follows:

f = 1 / (2π√(L_total * C_total))

Where L_total is the equivalent inductance of the parallel combination of L1 and L2, and C_total is the capacitance of C3. Understanding this relationship is fundamental for designing and analyzing Hartley oscillators in various applications, including signal generation and frequency synthesis.A popular circuit known as a Hartley oscillator. Its identifiable feature is the tapped coil in the LC tank circuit. Notice that the coil`s tap point is grounded. The amplifier portion of the oscillator is a common-emitter amplifier. Therefore, the ac base voltage and ac collector voltage are 180 out of phase. This means that the feedback network must provide an additional 180 phase shift so that the feedback voltage is of the correct phase to sustain oscillations. To help you understand the circuit`s operation, it has been redrawn in Fig. 2-2( b). Notice that L 1 is in parallel with L 2 and C 3 in series. At the resonant frequency of the tank circuit, the net reactance of the L 2 C 3 branch appears capacitive. Also, the net capacitive reactance of the L 2 C 3 branch equals the inductive reactance of the L 1 branch.

This gives us the following mathematical relationship. 🔗 External reference