Servo Circuit Controls Sine-Wave Amplitude

The figure illustrates a schematic for an oscillator amplitude-control servo system. The circuit establishes a closed-loop system that provides a fixed and adjustable peak-to-peak amplitude AC signal centered around 0 V. A 1 kHz sine wave, designated as AC_INPUT, is AC-coupled to an AD633 multiplier chip. The AC_INPUT is then multiplied by the SERVO signal. The output of the multiplier is a scaled version of the AC_INPUT. This 1 V sine output signal is directed into a peak detector, where the peak of the signal is compared to a user-supplied reference voltage. An error integrator processes the difference between the peak and the reference, generating the servo signal that feeds back into the multiplier. This servo signal adjusts the peak amplitude of the AD633 output to align with the user-supplied DC reference at the error integrator. The AC coupling of the input signal and the frequency of the input signal are flexible parameters. The circuit was successfully tested using a 1 kHz sine wave input with an amplitude of 4.5 V, resulting in a 1 V amplitude sine-wave output with a 1 V reference for the set point.

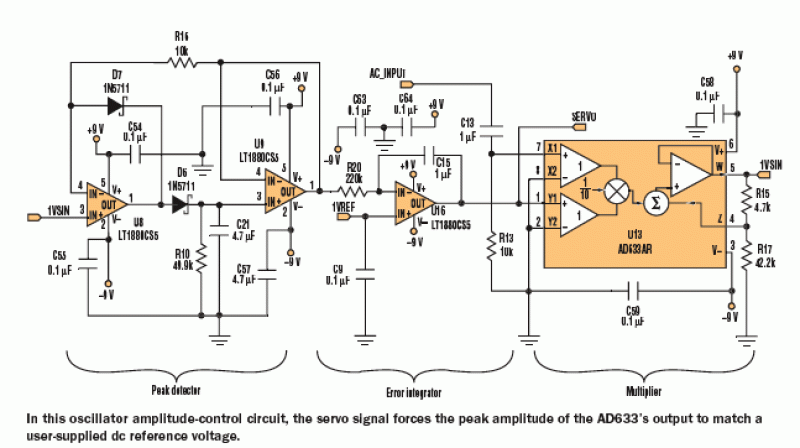
The oscillator amplitude-control servo system operates on the principle of feedback control to maintain a specified output amplitude. It consists of several key components, including an AD633 multiplier, a peak detector, an error integrator, and an adjustable reference voltage source. The AD633 multiplier is a versatile device that multiplies two input signals, in this case, the AC_INPUT and the SERVO signal. The output from the multiplier is a scaled version of the AC_INPUT, facilitating the generation of the desired output amplitude.

The peak detector is crucial for identifying the maximum value of the output waveform. It converts the AC signal into a DC voltage that corresponds to the peak amplitude of the sine wave. This DC voltage is then compared to a user-defined reference voltage, which serves as the target amplitude for the output signal. The difference between the detected peak and the reference voltage is processed by the error integrator, which accumulates this error over time to generate a corrective signal—the SERVO signal.

This SERVO signal is fed back into the multiplier, adjusting its output to ensure that the amplitude of the AC signal matches the reference voltage. This feedback loop allows for precise control of the output amplitude, making the system adaptable to various input conditions. The flexibility of the circuit is highlighted by its ability to operate with different input frequencies and amplitudes, as demonstrated in testing with a 1 kHz sine wave input at 4.5 V, which yielded a stable output of 1 V.

Overall, the oscillator amplitude-control servo system is an effective solution for applications requiring consistent and adjustable AC signal amplitudes, leveraging the principles of feedback control and signal processing to achieve its objectives.The figure shows a schematic for an oscillator amplitude-control servo system. The circuit creates a closed-loop system that supplies a fixed and adjustable peak-to-peak amplitude ac signal centered around 0 V. A 1-kHz sine wave, labeled AC_INPUT, is ac-coupled to an AD633 multiplier chip. Then the AC_INPUT is multiplied by the SERVO signal. The m

ultiplier`s output is a scaled version of the AC_INPUT. This 1-V sine output signal is fed into a peak detector, and the peak of the signal is compared to a user-supplied reference voltage. The error integrator integrates the difference between the peak and the reference. This generates the servo signal that feeds the multiplier. The servo signal will force the peak amplitude of the AD633 output to match that of the user-supplied dc reference at the error integrator.

The ac-coupling of the input signal and the frequency of the input signal are not fixed requirements. The circuit was successfully tested using a 1-kHz sine wave for the input with an amplitude of 4. 5 V, and it produced a 1-V amplitude sine-wave output using a 1-V reference for the set point.

🔗 External reference