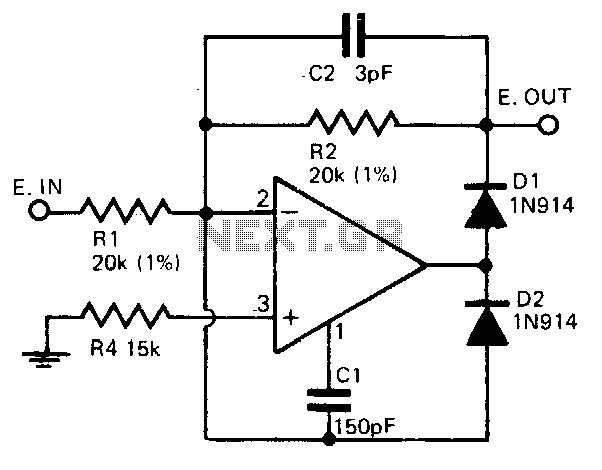
sine to square triangle wave

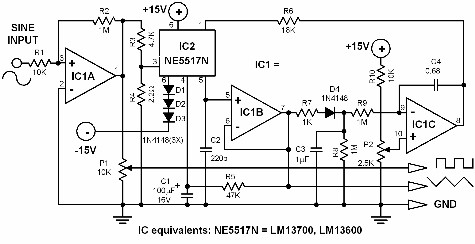
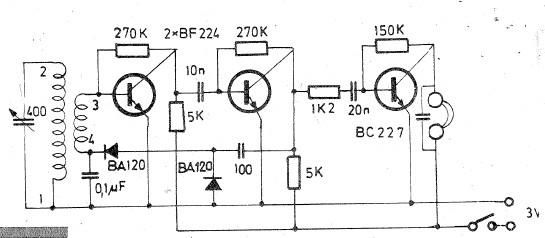
If a triangle wave signal or a square wave is required but only a sine wave generator is available, this converter can be utilized to simplify the process. The circuit consists of two integrated circuits (ICs): an LM13700 and a TL084. The amplitude of the square wave can be adjusted using potentiometer P1, while potentiometer P2 varies the amplitude of the triangle wave signal. The converter is capable of processing signals ranging from 6 Hz to 60 kHz. In many function generators, a triangle wave generator, typically composed of a Schmitt trigger combined with an integrator, serves as the core of the circuit. However, in this circuit, the sine wave is first reshaped into a triangle wave, which is subsequently converted to a square wave. It is important to note that the sine wave is not generated by this circuit and must be sourced externally. The sine wave is reshaped by operational amplifier IC1A, with resistors R3 and R4 reducing the output level of IC1A, which swings between -15 volts and +15 volts. The output from IC1A is then integrated by the transconductance amplifier IC1 and capacitor C2, with the integration time factor adjustable via a preset voltage level at pin 1 of IC1. Operational amplifier IC2B functions as an impedance converter, preventing voltage shifts at capacitor C2 that could occur due to overloading. The triangle wave can be sampled directly from the output of IC2B. The subsequent IC2C compares the amplitude of the triangle wave with a value preset by P2, and its output regulates the current at the output of IC1A. This method ensures that the output signal amplitude remains independent of the input signal frequency. Resistor R6 and capacitor C1 are configured in a feedback arrangement to precisely match the output level to the preset value from R4. This approach addresses the common issue of high-precision integrators being sensitive to offset voltages and stray currents, which can cause slight output signal variations. To maintain a clean resulting square wave, it is essential for the triangle wave to remain clean as well. A high time constant is selected for the RC circuit to ensure that the triangle wave does not influence the integrated waveform, even at low frequency levels. The converter can handle signals from 5 Hz with amplitude shifts of 0% to 60 kHz with amplitude shifts of -10%. At frequencies above 1 kHz, the circuit requires a longer stabilization time due to the high time constant levels of the RC circuits. The maximum amplitude of the source signal should be limited to 1 volt. The circuit can be powered with a battery, as its current consumption is approximately 10 mA.

The circuit design effectively transforms a sine wave input into both triangle and square wave outputs, utilizing a systematic approach to ensure signal integrity and stability across a wide frequency range. The choice of components, including the LM13700 and TL084, provides robust operational capabilities, while the use of potentiometers for amplitude control allows for versatile application in various electronic projects. The integration stage, facilitated by the transconductance amplifier and capacitor, is crucial for shaping the triangle wave, and the feedback mechanism involving resistors and capacitors is essential for maintaining precision in the output signal. The design's consideration of stray currents and offset voltages reflects a thorough understanding of the challenges associated with high-precision signal processing. Overall, this converter serves as a practical solution for generating triangle and square waveforms from a sine wave source, enabling a range of applications in electronics where such waveforms are required.If you need a triangle wave signal or a square one but you only have a sinewave generator, use this converter to avoid the trouble of beginning from scratch. It is made up of two ICs: one LM13700 and one TL084. The amplitude of the squarewave can be varied through P1 while potentiometer P2 varies the amplitude of the trianglewave signal.

The conve rter can process signals from 6 Hz up to 60 kHz. In many function generators, a triangle wave generator (which is usually made of a schmitt-trigger combined with an integrator) is the heart of the circuit. The resulting sine wave is then synthesized from the triangle wave with the help of special diode networks.

The circuit featured here, however, does it the other way around. First, the sinewave is reshaped to a triangle. Finally, the triangle is reshaped to a square wave. The sinewave is, however, not generated by this circuit. Therefore, you must get it from a sinewave source. The sinewave is reshaped by the opamp IC1A. The two resistors R3 and R4 reduce the output level of the IC1A, since this output level swings back and forth from negative 15 volts to positive 15 volts. The signal coming from IC1A is integrated by the combination of the transconductance amplifier IC1 and capacitor C2.

The integration time factor can be easily adjusted with a preset voltage level fed to pin 1 of IC1. The opamp IC2B is added to the circuit to act as an impedance converter. It prevents voltage shifts at the capacitor C2 that might happen due to overloading. The trianglewave can be sampled right from the output of IC2B. The following IC2C compares the trianglewave s amplitude with the value which is preset through P2. The output of IC2C controls the current regulator at the output of IC1A. This technique guarantees that the amplitude of the output signal remains independent from the input signal s frequency. The resistor R6 combined with the capacitor C1 play together so that the output level exactly matches the level that was preset by R4.

They are connected in a feedback manner. This technique solves the very common problem with high precision integrators - the sensitivity to offset voltages and stray currents. For example: a stray current (maximum: 7mA at 75 °C) can cause a slight change at the output signal. We want the resulting square wave to remain clean. That is why it is important the triangle wave must remain clean. To achieve it, the time constant of the RC circuit is selected to be high. This guarantees that the triangle wave can never influence the waveform to be integrated even at the lowest frequency levels.

This converter can process signals from 5 Hz with amplitude shifts of 0% up to 60 kHz with amplitude shifts of minus 10%. At higher frequencies - above 1 kHz - the circuit needs a longer time to stabilize itself. This is due to the high time constant levels of the RC circuits. You must set the maximal amplitude of the source signal to 1 volt. You can also use a battery to power the circuit since the current consumption is around 10 mA only. 🔗 External reference