Automotive Suspension with Analog Computing Methods
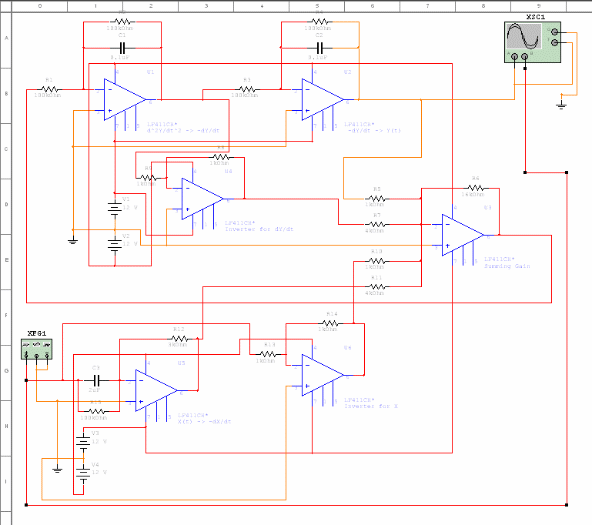
The analog computer was initially simulated using Multisim 7. Following this, an analog simulator circuit was constructed on breadboards using discrete and integrated components. A function generator was utilized to provide the road surface as input, and the output was monitored with an oscilloscope. The results confirm that the analog computer is an effective tool for accurately modeling second-order (and higher-order) systems. A car's suspension system can be represented by a simple mass-damper-spring model, where the mass symbolizes the vehicle's weight, the viscous friction element represents the shock absorber, and the standard spring is the remaining component. A free-body diagram of this system is presented, although it is a simplified model. In reality, a car rides on tires that possess their own spring constant, damping effect, and mass. For a more complex and accurate suspension model, refer to the Speed Bump Laboratory Assignment #4. For the current analysis, the simpler model is deemed adequate and will be modeled using the analog computer. To simulate the car traversing a bump, the road surface is allowed to "move" under the vehicle, with the height of the road at any time t serving as the input function to the system, x(t). The system's output, y(t), represents the movement of the mass (the car) as a function of the input. The differential equation for the system indicates that the vertical acceleration of the car (and its passengers) depends on the height of the road, the rate of change of the road height, and the suspension parameters. This model provides insight into the sensations experienced by passengers when driving over various bumps. For instance, driving over a sidewalk curb can be modeled as a step function input to the system, where the derivative of the input x(t) at t=0 behaves like an impulse function, resulting in a significant vertical acceleration transferred to the car body. Calculations show that even a small pothole in downtown Philadelphia (2cm x 10cm) can produce a vertical velocity of approximately 35 mph at the impact point when traversed by an average vehicle at 55 mph. In Laboratory Assignment 4, this system was modeled using Matlab Simulink, which functions as a simulated analog computer with integrators, differentiators, gains, and summation components. The differential equation can be rearranged to isolate the positive second derivative of y on the left side, displaying that dy/dt is the sum of several terms involving the parameters of the system. The process of designing an analog computer to simulate a differential equation begins with an integrator whose input is the highest-order derivative of the output. The output from the first integrator serves as the next highest-order derivative, continuing until the zeroth derivative term is reached. The outputs are then multiplied by the appropriate gains from the differential equation, summed, and fed back into the first integrator. The schematic for the Simulink circuit is provided. Operational amplifier integrated circuits are utilized to construct integrators, differentiators, gains, and summation units, allowing for the modeling of the car suspension differential equation in an analogous manner as in Simulink.
The analog computer simulation and subsequent construction of an analog circuit on breadboards provide a practical approach to understanding complex dynamic systems like a car's suspension. The mass-damper-spring model serves as a foundational representation, facilitating the analysis of how various parameters affect vehicle response. The use of a function generator to simulate road surface inputs allows for real-time observation of system behavior through an oscilloscope, enabling engineers to visualize the relationship between input and output.
The differential equation governing the system captures the essence of the dynamics involved, linking the physical properties of the suspension system to the forces experienced by passengers. This relationship is critical for designing vehicles that provide a comfortable ride while maintaining control and stability. By employing operational amplifiers to create the necessary components of the analog computer, engineers can effectively simulate the behavior of the suspension system and validate their models against real-world scenarios.
The insights gained from this modeling exercise can inform further developments in vehicle suspension design, leading to improvements in ride quality and safety. The ability to simulate various input conditions, such as driving over different types of bumps, enhances the understanding of passenger experiences and aids in optimizing suspension systems for diverse driving environments.The analog computer itself was first simulated on the computer with Multisim 7. Then, using discrete and integrated components, the analog simulator circuit was constructed on breadboards, and verified using a function generator to provide the road surface as input, and the output was observed using an oscilloscope. The results obtained clearly verify that the analog computer is a capable tool for accurate modeling of second order (and higher order) systems. A car`s suspension system can be modeled by a simple mass-damper-spring system. The mass represents the weight of the car sitting atop the suspension components. The viscous friction element representing the shock absorber and the standard spring comprise the remaining elements of the system.
A free-body diagram of the aforedescribed system is shown. Note that this is a somewhat simplified model. A car in real life rides on a tire that has some spring constant, damping effect, and mass itself. For discussion and analysis of a more complicated (but more accurate) model of suspension, refer to the Speed Bump Laboratory Assignment #4. For our purposes here, we will simply assume that the simpler model is "good enough" and we will model it using an analog computer.
To simulate the car going over a bump in the road, we let the road surface "move" under the car, and the height of the road at any time t is the input function to the system, x(t). The output of the system, y(t) is the movement of the mass (the car) as a function of the input. Writing the differential equation for the system, we get: Basically, the vertical acceleration of the car (and its passengers) is a function of the height of the road, how fast the height of the road changes, as well as the suspension parameters.
Based on this model, we can attain a sense of what a passenger feels when riding in a car over a variety of different bumps. For example, driving straight over a sidewalk curb could be modeled by a step function input to the system.
The derivative term of the input x(t) at t=0 is essentially an impulse function, meaning that a large vertical acceleration will be transferred to the car body. That is why when driving up onto a curb does a passenger feel a large jolt. Making some back-of-the-envelope calculations, we realize that even the smallest downtown Philadelphia pothole (a 2cm x 10cm bump), when driven over by an average Philadelphia policeman at 55 miles per hour, gives about a 35 mph straight vertical velocity transferred to the policemen at the impact point.
In Laboratory Assignment 4, we modeled this system using Matlab Simulink. Simulink is essentially a simulated analog computer with integrator, differentiator, gain, and summation components. We can reorganize the differential equation so that only the positive second derivative of y is present on the left hand side.
This way, we can see that dy/dt is simply the sum of (-b/m) * dy/dt, (-k/m) * y(t), (b/m)* dx/dt, and (k/m) * x(t). The idea behind designing an analog computer to simulate a differential equation is to start out with an integrator whose input is the highest order derivative of the output.
From there, the output of that first integrator is the next highest order derivative, and so on, until we have integrated our way to the zeroth derivative term. Then, we take those outputs, multiply them by the appropriate gains indicated by our differential equation, sum them, and send them back as the input to the first integrator.
The schematic for the Simulink circuit is given below. Operational amplifier integrated circuits can be used to create integrators, differentiators, gains, and summation units. Then, wiring the correct components together, we can model the car suspension differential equation analogously as in Simul
🔗 External reference
The analog computer simulation and subsequent construction of an analog circuit on breadboards provide a practical approach to understanding complex dynamic systems like a car's suspension. The mass-damper-spring model serves as a foundational representation, facilitating the analysis of how various parameters affect vehicle response. The use of a function generator to simulate road surface inputs allows for real-time observation of system behavior through an oscilloscope, enabling engineers to visualize the relationship between input and output.
The differential equation governing the system captures the essence of the dynamics involved, linking the physical properties of the suspension system to the forces experienced by passengers. This relationship is critical for designing vehicles that provide a comfortable ride while maintaining control and stability. By employing operational amplifiers to create the necessary components of the analog computer, engineers can effectively simulate the behavior of the suspension system and validate their models against real-world scenarios.
The insights gained from this modeling exercise can inform further developments in vehicle suspension design, leading to improvements in ride quality and safety. The ability to simulate various input conditions, such as driving over different types of bumps, enhances the understanding of passenger experiences and aids in optimizing suspension systems for diverse driving environments.The analog computer itself was first simulated on the computer with Multisim 7. Then, using discrete and integrated components, the analog simulator circuit was constructed on breadboards, and verified using a function generator to provide the road surface as input, and the output was observed using an oscilloscope. The results obtained clearly verify that the analog computer is a capable tool for accurate modeling of second order (and higher order) systems. A car`s suspension system can be modeled by a simple mass-damper-spring system. The mass represents the weight of the car sitting atop the suspension components. The viscous friction element representing the shock absorber and the standard spring comprise the remaining elements of the system.
A free-body diagram of the aforedescribed system is shown. Note that this is a somewhat simplified model. A car in real life rides on a tire that has some spring constant, damping effect, and mass itself. For discussion and analysis of a more complicated (but more accurate) model of suspension, refer to the Speed Bump Laboratory Assignment #4. For our purposes here, we will simply assume that the simpler model is "good enough" and we will model it using an analog computer.
To simulate the car going over a bump in the road, we let the road surface "move" under the car, and the height of the road at any time t is the input function to the system, x(t). The output of the system, y(t) is the movement of the mass (the car) as a function of the input. Writing the differential equation for the system, we get: Basically, the vertical acceleration of the car (and its passengers) is a function of the height of the road, how fast the height of the road changes, as well as the suspension parameters.
Based on this model, we can attain a sense of what a passenger feels when riding in a car over a variety of different bumps. For example, driving straight over a sidewalk curb could be modeled by a step function input to the system.
The derivative term of the input x(t) at t=0 is essentially an impulse function, meaning that a large vertical acceleration will be transferred to the car body. That is why when driving up onto a curb does a passenger feel a large jolt. Making some back-of-the-envelope calculations, we realize that even the smallest downtown Philadelphia pothole (a 2cm x 10cm bump), when driven over by an average Philadelphia policeman at 55 miles per hour, gives about a 35 mph straight vertical velocity transferred to the policemen at the impact point.
In Laboratory Assignment 4, we modeled this system using Matlab Simulink. Simulink is essentially a simulated analog computer with integrator, differentiator, gain, and summation components. We can reorganize the differential equation so that only the positive second derivative of y is present on the left hand side.
This way, we can see that dy/dt is simply the sum of (-b/m) * dy/dt, (-k/m) * y(t), (b/m)* dx/dt, and (k/m) * x(t). The idea behind designing an analog computer to simulate a differential equation is to start out with an integrator whose input is the highest order derivative of the output.
From there, the output of that first integrator is the next highest order derivative, and so on, until we have integrated our way to the zeroth derivative term. Then, we take those outputs, multiply them by the appropriate gains indicated by our differential equation, sum them, and send them back as the input to the first integrator.
The schematic for the Simulink circuit is given below. Operational amplifier integrated circuits can be used to create integrators, differentiators, gains, and summation units. Then, wiring the correct components together, we can model the car suspension differential equation analogously as in Simul
🔗 External reference
Related Circuits
Normally analogue-to-digital converter (ADC) needs interfacing through a microprocessor to convert analogue data into digital format. This requires hardware and necessary software, resulting in increased complexity and hence the total cost. The circuit of A-to-D converter shown here is...
This circuit is used to measure the voltage on a 12V (nominal) lead acid rechargeable battery system. It was specifically designed for use in solar powered systems, but is general enough that it can be used for automotive or...
A clock-and-data recovery (CDR) circuit is utilized to recover the clock from a transmitted data stream and re-time that data with the recovered clock. These circuits are generally positioned at the front-end of receiver chips to extract the clock...
This simple circuit utilizes an LM311 as a level detector, incorporating CMOS analog switches to control capacitance. A significant feature of this counter is its ability to change numbers. The comparator operates more efficiently when there is a need...
This automotive battery charger project is designed to charge 12V electrolyte lead-acid batteries. The automotive battery charger circuit is engineered to efficiently charge 12V lead-acid batteries, which are commonly used in vehicles. The design typically incorporates several key components, including...
The number of silicon diodes across the output is determined by the voltage of the battery pack. Each diode is considered at 0 volts. For example, a 10-volt pack would require 10/0 = 157, or 16 diodes. In the context...