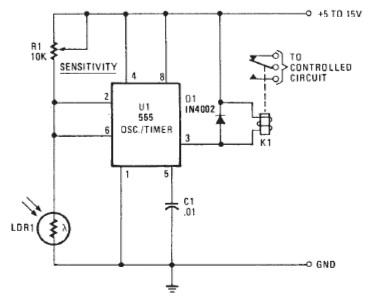
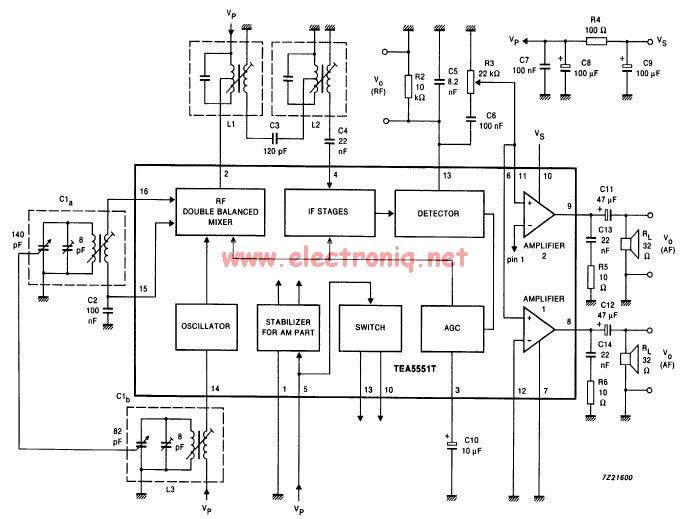
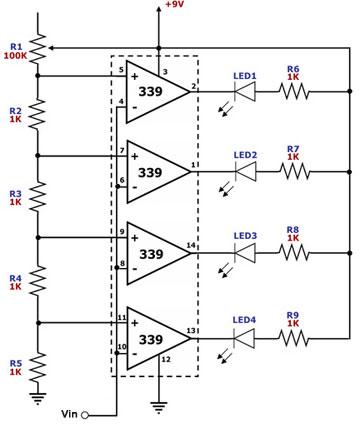
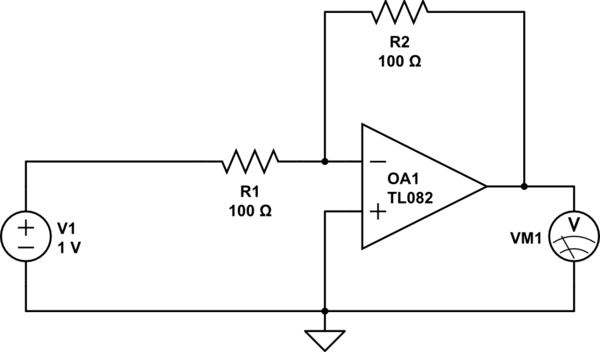
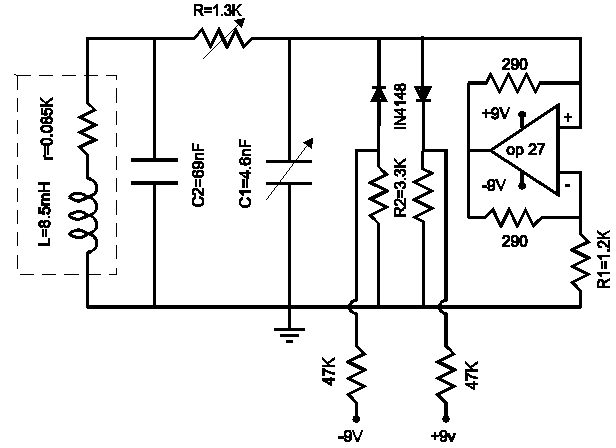
Chua's Oscillator circuit

The applet shows a simulation of Chua's circuit, plotting the voltage measured across C1 against the voltage measured across C2. This corresponds to the display on an X-Y oscilloscope with probes connected across these capacitors. The initial values of the parameters used in the applet correspond to the component values in the circuit diagram, and show a simple periodic orbit (oscillation). The transition to chaotic dynamics can be found by carefully decreasing R or C1, (e.g. decrease R in steps of 0.01 to 1.2K). The simulation compares well with what is actually seen on an oscilloscope. Chaos seems to develop via a subharmonic cascade. If you do not have access to an oscilloscope, you can use the voltage across C1 or C2 as the input to a high input impedance audio amplifier (with the component values shown the frequency of the oscillations is in the audio range). It turns out that the ear is very sensitive to the development of a weak subharmonic. The subharmonic becomes the fundamental an octave below the original tone, and the ear hears the note drop an octave even when the intensity of the new fundamental is very weak. The first two or three transitions in the subharmonic cascade route to chaos, and the onset of chaos (noise!) are very audible.

Chua's circuit is a well-known example of a nonlinear electronic oscillator that exhibits chaotic behavior under certain conditions. The circuit typically consists of a nonlinear resistor (Chua's diode), two capacitors (C1 and C2), and an inductor, along with resistors that define the circuit's parameters. The voltage across the capacitors is a critical aspect of the circuit's operation, as it illustrates the relationship between energy storage in the capacitors and the nonlinear dynamics of the circuit.

In the described applet simulation, the X-Y oscilloscope representation allows for a visual analysis of the circuit's behavior by plotting the voltage across C1 against that across C2. This graphical representation reveals the oscillatory nature of the circuit, where periodic orbits indicate stable oscillations. As the resistance (R) or capacitance (C1) is varied, the circuit transitions from periodic oscillations to chaotic dynamics. This transition is characterized by a subharmonic cascade, where the system's frequency components become increasingly complex, leading to chaotic noise.

For practical applications, if an oscilloscope is unavailable, the voltage outputs from C1 or C2 can be routed to a high-impedance audio amplifier. This approach allows for auditory observation of the oscillations, as the frequencies produced by the circuit fall within the audible range. The human ear can detect subtle changes in frequency, particularly the emergence of subharmonic tones, which can create an auditory experience of chaos as the circuit's dynamics evolve. The perception of these subharmonics, even at low intensities, highlights the sensitivity of human hearing to complex waveforms and chaotic behavior in electronic circuits. The initial transitions in the subharmonic cascade are particularly significant, as they mark the onset of chaos and can be perceived as a notable change in tone, providing an engaging way to explore the dynamics of Chua's circuit.The applet shows a simulation of Chua's circuit, plotting the voltage measured across C1 against the voltage measured across C2. This corresponds to the display on an X-Y oscilloscope with probes connected across these capacitors.

The initial values of the parameters used in the applet correspond to the component values in the circuit diagram, and show a simple periodic orbit (oscillation). The transition to chaotic dynamics can be found by carefully decreasing R or C1, (e.g. decrease R in steps of 0.01 to 1.2K). The simulation compares well with what is actually seen on an oscilloscope. Chaos seems to develop via a subharmonic cascade. If you do not have access to an oscilloscope, you can use the voltage across C1 or C2 as the input to a high input impedance audio amplifier (with the component values shown the frequency of the oscillations is in the audio range). It turns out that the ear is very sensitive to the development of a weak subharmonic. The subharmonic becomes the fundamental an octave below the original tone, and the ear hears the note drop an octave even when the intensity of the new fundamental is very weak.

The first two or three transitions in the subharmonic cascade route to chaos, and the onset of chaos (noise!) are very audible. 🔗 External reference