Measuring Inductors

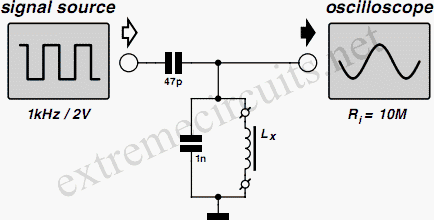
Often, there are instances where it becomes necessary to wind a coil for a project or to identify an unmarked coil found in a collection. To determine its inductance, an oscilloscope can be utilized. A resonant circuit can be constructed using the coil and a capacitor, which is then connected to a square wave generator (often integrated into the oscilloscope). By adjusting the generator, the resonant frequency (f) can be found. Given a known capacitance (for example, 1000 pF), the inductance (L) can be calculated using the formula: L = 1 / (4π²f²C). Additionally, if the quality factor (Q) of the coil is of interest, the oscilloscope can be employed once more. If the amplitude of the damped oscillation decreases to approximately 0.37 (which is 1/e) of the maximum after about 30 cycles, the Q factor of the coil is estimated to be around 30. It is important to measure the Q factor at the coil's intended operating frequency and with the appropriate capacitor, while the coupling capacitor should be significantly smaller in value.

To determine the inductance of a coil effectively, a resonant circuit can be constructed. This circuit typically consists of the coil and a capacitor connected to a square wave generator, which can often be part of an oscilloscope setup. The process begins by adjusting the square wave generator to find the resonant frequency (f) of the circuit. The resonant frequency is the point at which the inductive reactance of the coil and the capacitive reactance of the capacitor are equal, resulting in maximum current flow through the circuit.

Once the resonant frequency is established, the inductance (L) of the coil can be calculated using the formula L = 1 / (4π²f²C), where C represents the capacitance of the capacitor used in the circuit. For instance, if a capacitor value of 1000 pF is employed, substituting this value along with the measured resonant frequency into the formula will yield the inductance of the coil.

In addition to determining the inductance, the quality factor (Q) of the coil can also be assessed using the oscilloscope. The Q factor is a measure of the coil's efficiency and is indicative of how well the coil can store energy compared to how much energy is lost. To evaluate the Q factor, observe the damped oscillations on the oscilloscope. If the amplitude of these oscillations decreases to approximately 0.37 of the maximum value after about 30 cycles, the Q factor can be estimated to be around 30. It is crucial to perform this measurement at the intended operating frequency of the coil and with the appropriate capacitor to ensure accurate results. Furthermore, the coupling capacitor used in this measurement should be significantly smaller than the main capacitor to avoid influencing the Q factor measurement. This method provides a reliable approach to characterizing coils for various electronic applications.Often you find yourself in the position of needing to wind your own coil for a project, or maybe you come across an unmarked coil in the junk-box. How can you bestnd out its inductance An oscilloscope is all you need. Construct a resonant circuit using the coil and a capacitor and connect it to a square wave generator (often part of the oscil

loscope itself) Adjust the generator until you find the resonant frequency f. When C is known (1000pF) the inductance L may be calculated from: L=1/(4 2. f2. C) If you are also interested how good the coil is i. e. what is its quality factor or Q, you can use the oscilloscope again. If the level of the damped oscillation drops to 0. 37 (= 1/e) of the maximum after about 30 periods, then the Q factor of the coil is about 30. The Q factor should be measured at the intended operating frequency of the coil and with its intended capacitor. The coupling capacitor should by comparison be a much smaller value. 🔗 External reference