Nonlinear Oscillator
The purpose of this experiment is to explore the properties of a nonlinear circuit that closely resembles a driven pendulum. This serves as an excellent introduction to nonlinear phenomena, including period doubling and chaos. The circuit presented is an enhancement of previous designs and is discussed in the section titled "Analysis of the Phase Locked Loop Circuit." A recommended sequence of steps for conducting the laboratory experiment is provided, along with guidance on operating parameters and methodologies. Familiarity with the TDS220 oscilloscope and the HP 35660A Dynamic Signal Analyzer is encouraged. Key measurements include the frequency response of the low pass filter and integrator modules, as well as parameters essential for understanding the circuit's behavior. The assembly of the phase locked loop (PLL) modules follows a specified block diagram, with attention to the correct connections and configurations. Monitoring and adjusting the reference wave amplitude and frequency are crucial for determining the locking range of the PLL.
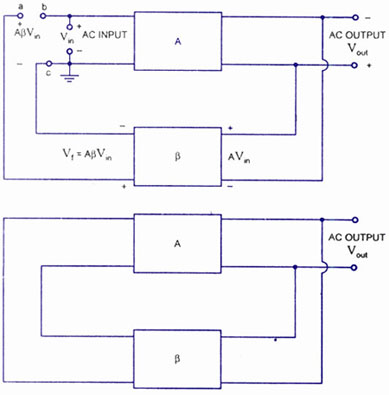
The experiment aims to investigate the dynamics of a nonlinear circuit that simulates a driven pendulum, emphasizing the study of chaotic behavior and period doubling. The circuit's design builds upon previous works, specifically enhancing the phase locked loop (PLL) configuration. The PLL is a critical component in this setup, as it allows for the synchronization of the output frequency with an input reference signal, demonstrating key principles of nonlinear dynamics.
To initiate the experiment, the TDS220 oscilloscope must be set up to visualize the circuit's behavior. Understanding how to manipulate the oscilloscope's trigger settings and scaling options is vital for capturing accurate waveforms. The HP 35660A Dynamic Signal Analyzer should also be utilized to analyze the frequency response of the circuit components, particularly the low pass filter and integrator modules. These measurements provide insights into the circuit's performance and its ability to maintain synchronization under various conditions.
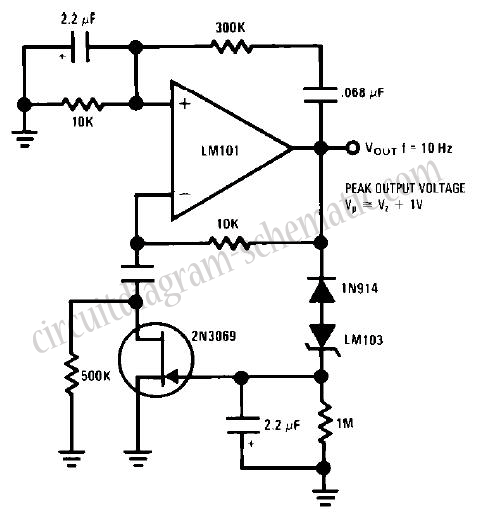
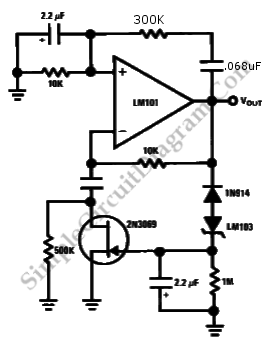
The assembly of the PLL modules should adhere to the provided block diagram, ensuring that one input of the integrator remains unused for future signal connections. The Wavetek 171 signal generator is connected through a switch-controlled attenuator to the reference input of the mixer, allowing for precise control over the reference wave amplitude and frequency. Careful monitoring of the reference wave's amplitude, set to -1.3 dBVrms or 860 mVrms, is essential as it directly influences the PLL's locking behavior.
During the experiment, the frequency range over which the PLL locks should be determined by systematically adjusting the frequency of the reference generator while observing the clock output of the VCO on the oscilloscope. The feedback resistance of the integrator should be set to 7700 ohms, as this value has been found to yield reasonable locking conditions. Observations should be made regarding the hysteresis effects around the locking range, as these can significantly impact the stability of the PLL.
It is advisable to approach the edges of the locking range cautiously to avoid losing synchronization. The experiment encourages exploration and experimentation with different configurations and parameters, allowing for a deeper understanding of the nonlinear dynamics involved. Additionally, the use of an oscilloscope to visualize the phase space motion of the simulated pendulum can enhance comprehension of chaotic behavior within the system.
Overall, this experiment provides a comprehensive examination of a nonlinear circuit modeled after a driven pendulum, offering valuable insights into the principles of chaos and synchronization in dynamical systems.The purpose of this experiment is to discover the properties of a nonlinear circuit which closely approximates a driven pendulum. It`s a great introduction to nonlinear phenomena such as period doubling and chaos. "Chaotic States and Routes to Chaos in the Forced Pendulum, " by D. D`Humieres, M. R. Beasley, B. A. Huberman, and A. Libchaber, Phys. Re v. A 26 3483 (1982). Our circuit is an improvement on theirs and is described in the section "Analysis of the Phase Locked Loop Circuit". Excerpts from Order Within Chaos by P. Berge, Y. Pomeau, and C. Vidal (Hermann and Wiley, Paris, 1984). This reference includes an introduction to the modem physics of dynamical systems. The following is a recommended sequence of steps for a long laboratory. Do not feel restricted to the operating parameters quoted in these notes, or even the methodology. Their main purpose is to help you get your feet wet. There is an enormous amount of investigation that can be done in this experiment, so feel free to focus on the parts you find most interesting, and also try out new ideas as they occur to you.
Familiarize yourself with the TDS220 oscilloscope if you have not used one before. Learn how to view and scale traces, how to manipulate the trigger settings, and how to use the cursors. The scope also has useful functions under the "measure" menu. Look over the "Getting Started Guide" for the HP 35660A Dynamic Signal Analyzer. Look at the spectrum and the time series measurement for the signal source running as a sine wave, a periodic chirp, and a random noise source.
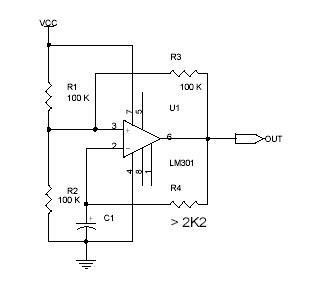
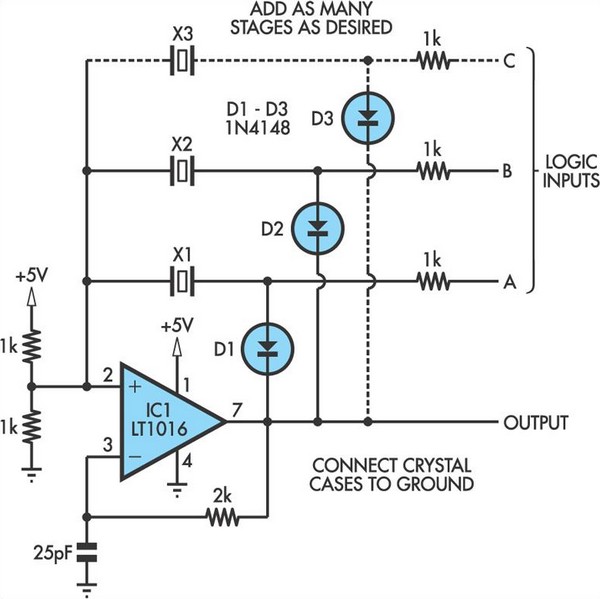
Measure the frequency response of the low pass filter and the integrator modules of the oscillator. The procedure is described in Chapter 8 of the analyzer guide. Measure f0( = ‰0 / 2 ), the VCO frequency when the input is 0V (or shorted), and k( = ’ d ‰out / dVin), by applying a DC voltage to the VCO input (labeled "cont") and viewing the "clock" output on the spectrum analyzer. These are important parameters for understanding the circuit. Assemble the modules of the phase locked loop (PLL) following the block diagram below. Leave one input of the integrator unused; the drive signal will go there later. (Note: opening and shorting some terminals on this circuit give equivalent results, such as the integrator and VCO inputs.
However, the mixer will behave strangely if the "sine" input is left open. ) Next, connect the Wavetek 171 through a switch-controlled attenuator to the reference sine wave input of the mixer. It is useful to connect the same signal to a digital AC voltmeter for monitoring during the experiment.
Set the reference wave to an amplitude of -1. 3 dBVrms (measured on the spectrum analyzer) or 860 mVrms (measured on the voltmeter) while the frequency, fs( = ‰s / 2 ) is near f0. Find the frequency over which the PLL locks as follows: Externally trigger the scope from the sync output of the reference wave generator.
Monitor the output of the PLL by looking at the clock output of the VCO on the scope. Set the feedback resistance control on the integrator (R) to 7700. Scan the frequency of the generator and note the range of locking. Scan the R control on the integrator, noting the range over which locking occurs. You should compare the locking range with that expected (see the "Equilibrium Phase and Conditions for Locking" subsection below). There is substantial hysteresis near the edges of the locking range. If the PLL becomes unlocked because you took too large a step in reference frequency you should return to the center of the locking range and approach the edges more cautiously.
Reasonable settings for most of the measurements are: R = 7700, reference wave amplitude = 860 mVrms, fs = fL. You might enjoy learning about PLLs and their applications in the excerpt from The Art of Electronics.
An oscilloscope can be connected so that you can watch the phase space motion of the pendulum being simulated. The integrato 🔗 External reference
The experiment aims to investigate the dynamics of a nonlinear circuit that simulates a driven pendulum, emphasizing the study of chaotic behavior and period doubling. The circuit's design builds upon previous works, specifically enhancing the phase locked loop (PLL) configuration. The PLL is a critical component in this setup, as it allows for the synchronization of the output frequency with an input reference signal, demonstrating key principles of nonlinear dynamics.
To initiate the experiment, the TDS220 oscilloscope must be set up to visualize the circuit's behavior. Understanding how to manipulate the oscilloscope's trigger settings and scaling options is vital for capturing accurate waveforms. The HP 35660A Dynamic Signal Analyzer should also be utilized to analyze the frequency response of the circuit components, particularly the low pass filter and integrator modules. These measurements provide insights into the circuit's performance and its ability to maintain synchronization under various conditions.
The assembly of the PLL modules should adhere to the provided block diagram, ensuring that one input of the integrator remains unused for future signal connections. The Wavetek 171 signal generator is connected through a switch-controlled attenuator to the reference input of the mixer, allowing for precise control over the reference wave amplitude and frequency. Careful monitoring of the reference wave's amplitude, set to -1.3 dBVrms or 860 mVrms, is essential as it directly influences the PLL's locking behavior.
During the experiment, the frequency range over which the PLL locks should be determined by systematically adjusting the frequency of the reference generator while observing the clock output of the VCO on the oscilloscope. The feedback resistance of the integrator should be set to 7700 ohms, as this value has been found to yield reasonable locking conditions. Observations should be made regarding the hysteresis effects around the locking range, as these can significantly impact the stability of the PLL.
It is advisable to approach the edges of the locking range cautiously to avoid losing synchronization. The experiment encourages exploration and experimentation with different configurations and parameters, allowing for a deeper understanding of the nonlinear dynamics involved. Additionally, the use of an oscilloscope to visualize the phase space motion of the simulated pendulum can enhance comprehension of chaotic behavior within the system.
Overall, this experiment provides a comprehensive examination of a nonlinear circuit modeled after a driven pendulum, offering valuable insights into the principles of chaos and synchronization in dynamical systems.The purpose of this experiment is to discover the properties of a nonlinear circuit which closely approximates a driven pendulum. It`s a great introduction to nonlinear phenomena such as period doubling and chaos. "Chaotic States and Routes to Chaos in the Forced Pendulum, " by D. D`Humieres, M. R. Beasley, B. A. Huberman, and A. Libchaber, Phys. Re v. A 26 3483 (1982). Our circuit is an improvement on theirs and is described in the section "Analysis of the Phase Locked Loop Circuit". Excerpts from Order Within Chaos by P. Berge, Y. Pomeau, and C. Vidal (Hermann and Wiley, Paris, 1984). This reference includes an introduction to the modem physics of dynamical systems. The following is a recommended sequence of steps for a long laboratory. Do not feel restricted to the operating parameters quoted in these notes, or even the methodology. Their main purpose is to help you get your feet wet. There is an enormous amount of investigation that can be done in this experiment, so feel free to focus on the parts you find most interesting, and also try out new ideas as they occur to you.
Familiarize yourself with the TDS220 oscilloscope if you have not used one before. Learn how to view and scale traces, how to manipulate the trigger settings, and how to use the cursors. The scope also has useful functions under the "measure" menu. Look over the "Getting Started Guide" for the HP 35660A Dynamic Signal Analyzer. Look at the spectrum and the time series measurement for the signal source running as a sine wave, a periodic chirp, and a random noise source.
Measure the frequency response of the low pass filter and the integrator modules of the oscillator. The procedure is described in Chapter 8 of the analyzer guide. Measure f0( = ‰0 / 2 ), the VCO frequency when the input is 0V (or shorted), and k( = ’ d ‰out / dVin), by applying a DC voltage to the VCO input (labeled "cont") and viewing the "clock" output on the spectrum analyzer. These are important parameters for understanding the circuit. Assemble the modules of the phase locked loop (PLL) following the block diagram below. Leave one input of the integrator unused; the drive signal will go there later. (Note: opening and shorting some terminals on this circuit give equivalent results, such as the integrator and VCO inputs.
However, the mixer will behave strangely if the "sine" input is left open. ) Next, connect the Wavetek 171 through a switch-controlled attenuator to the reference sine wave input of the mixer. It is useful to connect the same signal to a digital AC voltmeter for monitoring during the experiment.
Set the reference wave to an amplitude of -1. 3 dBVrms (measured on the spectrum analyzer) or 860 mVrms (measured on the voltmeter) while the frequency, fs( = ‰s / 2 ) is near f0. Find the frequency over which the PLL locks as follows: Externally trigger the scope from the sync output of the reference wave generator.
Monitor the output of the PLL by looking at the clock output of the VCO on the scope. Set the feedback resistance control on the integrator (R) to 7700. Scan the frequency of the generator and note the range of locking. Scan the R control on the integrator, noting the range over which locking occurs. You should compare the locking range with that expected (see the "Equilibrium Phase and Conditions for Locking" subsection below). There is substantial hysteresis near the edges of the locking range. If the PLL becomes unlocked because you took too large a step in reference frequency you should return to the center of the locking range and approach the edges more cautiously.
Reasonable settings for most of the measurements are: R = 7700, reference wave amplitude = 860 mVrms, fs = fL. You might enjoy learning about PLLs and their applications in the excerpt from The Art of Electronics.
An oscilloscope can be connected so that you can watch the phase space motion of the pendulum being simulated. The integrato 🔗 External reference
Related Circuits
The circuit consists of two oscillators, both working at about 465 kHz. One uses an if transformer and the other uses an inductor (the search coil LI). The oscillators are coupled by a capacitor (10 pF). A beat note...
The circuit is designed exclusively for fundamental crystals, as it lacks mode suppression components. The oscillator transistor Q104 remains in a cutoff state for most of the time, activating only briefly during the peak of the crystal current waveform....
Colpitts oscillators are similar to the shunt-fed Hartley circuit; however, the Colpitts oscillator uses two series capacitors in its LC circuit instead of a tapped inductor. The connection between these two capacitors serves as the center tap for the...
Figure a illustrates a multivibrator circuit capable of generating a square wave signal. Figure b depicts a flip-flop circuit that utilizes the falling edge of the input signal to produce a trigger pulse signal. Figure c represents a monostable...
The first thing to understand is how capacitor C1 is related to the resonance frequency f of the circuit. It appears that selecting a frequency allows for the automatic determination of the necessary value for C1. There are uncertainties...
An op-amp Hartley oscillator was created using an electronics simulator; however, despite successful simulation, no oscillation is observed. The Hartley oscillator is a type of electronic oscillator that generates sine waves. It typically consists of an operational amplifier (op-amp) configured...